不完全信道统计信息反馈下的MIMO系统容量
2019-05-05罗敬原
杜 维,罗敬原,周 雯
(南京林业大学 信息科技学院,江苏 南京 210018)
0 引言
MIMO系统在发射端和接收端均配备了多个天线,可以充分利用空间资源,将通信链路分解成许多并行的子信道,大幅度提高了系统的数据传输速率,已经成为第四代(4G)和第五代(5G)无线通信系统的核心技术[1-2]。而5G在4G研究的基础上,提出了大规模MIMO的概念,进一步提升系统容量和增加小区覆盖范围。
MIMO系统的容量问题一直是国内外的研究热点,其中基于信道状态信息(Channel State Information,CSI)反馈的系统容量是该类问题研究的重要内容。基于CSI反馈的系统中,发送端利用接收端反馈的CSI,可以进行波束成形、功率控制与自适应调制等操作,有效地提升系统数据传输速率或改善误码率性能[3-11]。一般CSI反馈分为2种:即时CSI反馈和统计CSI反馈。若信道变化缓慢,采用即时CSI反馈较为合适,文献[3]采用即时CSI信息,针对放大转发MIMO中继系统设计了收发器。若信道变化迅速,采用即时CSI反馈不再合适,因为频繁的信道信息反馈将增加系统的负荷,此时采用统计CSI反馈方式较为合适。例如,文献[4]研究了基于信道均值和协方差反馈的MIMO中继系统最优发送策略,文献[5]在假设发送端具备信道协方差信息的情况下,给出了最优发送协方差矩阵的结构。
考虑到反馈信道存在噪声干扰和导频长度有限等因素的影响,即时反馈的CSI通常是有误差的,有些文献研究了不完全即时CSI反馈的MIMO系统容量[6-9]。例如,文献[6]研究了基于有误即时CSI反馈的MIMO网络中干扰对齐策略。文献[9]基于不完全信道信息反馈推导系统的成对误差概率,研究了认知多天线系统的正交空域调制技术。另一方面,信道统计信息通常由系统接收端经过一段时间测量得到,然而接收端测量使用的信道样本数目有限,反馈信道通常也存在噪声,因此反馈的信道统计信息是有误的。如果无线信道是非平稳的,其统计特性随时间缓慢变化,则反馈的信道统计信息可能存在延时误差。目前,基于有误统计CSI反馈的MIMO容量分析较少见,大多数考虑有误即时CSI反馈对系统的影响。
本文针对反馈信道中受多种因素影响而产生的有误CSI反馈,建立闭环MIMO系统模型,推导相应的闭环系统容量公式,定义反馈信噪比和相应的门限。仿真实验对比了若干典型信道反馈方式下的MIMO系统容量,分析反馈信噪比对于系统容量的影响,在若干系统配置下,给出了反馈信噪比门限,这对系统的设计有指导意义。
1 系统模型
闭环MIMO系统模型如图1所示。
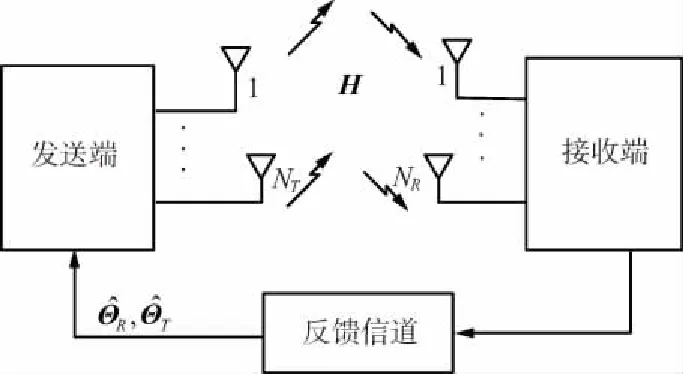
图1 闭环MIMO系统模型
发送端和接收端均配备多根天线,数目分别为NT和NR。利用反馈的信道统计信息,发送端计算预编码矩阵W,将用户数据X与之相乘发送出去。信号经过无线信道H到达接收端,假设信道H是平坦衰落的,则接收信号y可以表示为:
y=HWx+n,
(1)
(2)
式中,ΘR和ΘT分别表示接收端和发送端的信道相关矩阵,均是正定的Hermite矩阵,且满足Tr(ΘR)=NR和Tr(ΘT)=NT,Tr(· )代表矩阵求迹。
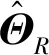
(3)
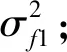
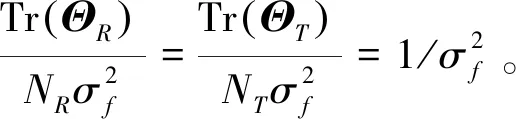
(4)
为了对系统进行整体性能评估,定义闭环MIMO系统的信噪比为:
SNR≜P/σ2,
(5)
式中,P为发送总功率。
2 闭环MIMO系统容量和反馈信噪比下限
2.1 开环容量
如果发送端不知道信道状态信息,则最优的预编码矩阵是单位阵,每根天线的数据子流应采用等功率分配,此时系统的开环容量为:
(6)
式中,符号E(·)代表数学期望,(·)H为矩阵的Hermitian转置运算。
2.2 基于完全统计CSI反馈的闭环容量
如果发送端得到的统计CSI是完全的,即得到的2个信道相关矩阵没有误差,则最优发送信号协方差矩阵Q的特征向量构成的矩阵UQ满足[18]:
UQ=UΘT,
(7)
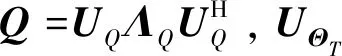
Q=E[(Wx)(Wx)H]=WWH。
(8)
利用ΘT和ΘR,最优功率分配矩阵ΛQ可以通过遍历搜索法[16]或文献[17]提出的接近最优功率分配方法得出。这样最优发送协方差矩阵Q可以由式(8)求出,系统的闭环容量为:
(9)
式中,ΛΘR是ΘR特征分解中的对角阵。
2.3 基于不完全统计CSI反馈的闭环容量
如图1所示,当发送端得到的统计CSI是不完全的,即反馈的2个信道相关矩阵存在误差,为了减小误差的影响,首先做如下操作:
(10)
式中,符号=:代表赋值运算,这样可以保证信道相关矩阵是Hermite矩阵,然后做归一化操作:

(11)


(12)
预编码矩阵可以表示为:
(13)
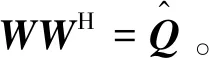
(14)
整个系统的运作流程归纳如下:
④ 根据式(13)求出预编码矩阵W,与用户数据x相乘发送出去。
3 反馈信噪比门限
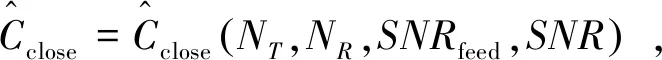
Copen(NT,NR,SNR)]。
(15)
4 仿真结果
采用数值仿真方法研究了不完全统计CSI下的MIMO系统容量。信道采用MIMO Kronecker模型,其中的信道收发相关矩阵采用指数模型[19-20],矩阵的第(i,j)个元素是ρ|i-j|,0<ρ<1是常数。对于收发相关矩阵,均设定ρ=0.5。MIMO系统的开环容量采用式(6)计算,理想统计CSI反馈的系统容量采用式(11)计算,非理想统计CSI反馈的容量采用式(16)计算。
4.1 反馈信噪比对系统容量的影响
图2描述了不同反馈信噪比下的系统容量,系统的天线数目NT=NR=2。考虑了2种系统信噪比情况,分别对比了有误统计CSI反馈、无误统计CSI反馈和开环3种情况下的系统容量。
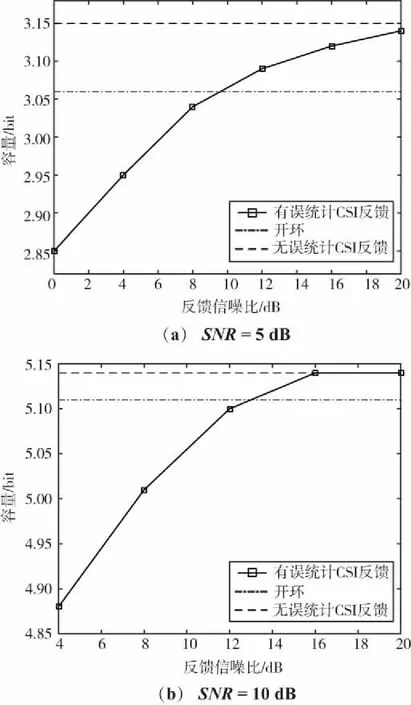
图2 不同反馈信噪比下的系统容量
由图2可以看到,随着反馈信噪比SNRfeed的增加,有误统计CSI反馈下的系统容量也随着增加;在反馈信噪较小时,系统容量可能小于开环容量。例如,对于SNR=5 dB,当反馈信噪比大约低于9.3 dB时,有误统计CSI反馈下系统容量小于开环容量3.06 bit;随着反馈信噪比的增加,系统容量逐渐增加并接近上限3.15 bit,这也是理想统计CSI反馈的容量。当SNR=10 dB时,也出现类似现象。
图2表明,在系统设计时,当反馈信噪比门限高于某个值的时候,闭环系统容量相对开环容量才有正增益,此时的反馈才有意义。
4.2 不同反馈方式的系统容量
图3对比了不同系统配置下若干反馈方式的容量,其中图3(a)为3×3系统,图3(b)为4×4系统。考虑了4种反馈方式,包括有误统计CSI反馈、无误统计CSI反馈、无误即时CSI反馈和开环(不反馈)方式。
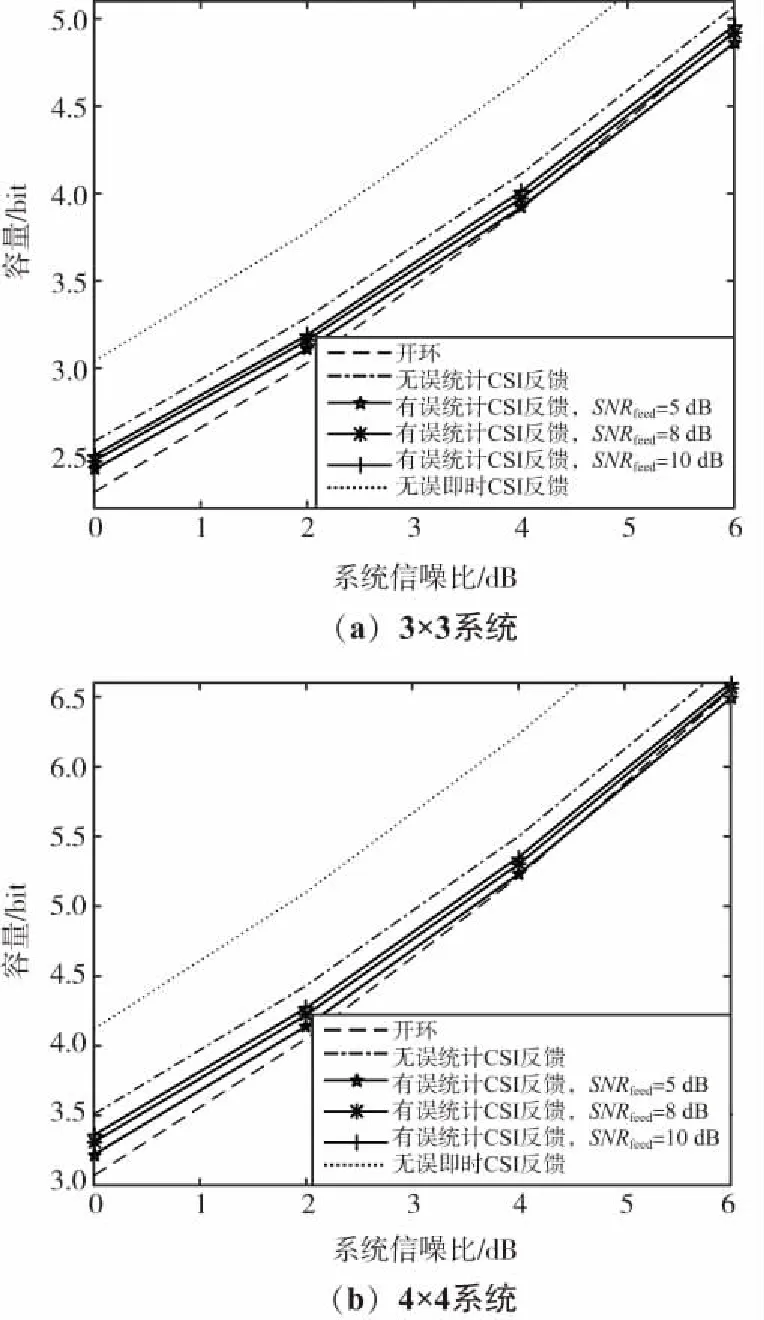
图3 不同反馈方式的系统容量对比
整体而言,可以发现无误即时CSI反馈容量远高于其他几种方法,这是因为发送端知道每一时刻的信道状态信息;相比其他方式,该反馈方式的反馈信息量最大。对于有误统计CSI反馈,随着反馈信噪比的增加,曲线整体上移,即给定系统信噪比,系统容量随反馈信噪比增加而增加。如图3(a)所示,当系统信噪比是2 dB时,反馈信噪比5,8,10 dB对应的系统容量分别是3.11,3.16,3.19 bit。而且,随着反馈信噪比的增加,有误统计CSI的系统容量逐渐逼近其上限——无误统计CSI反馈的容量。还发现,在低系统信噪比时,有误统计CSI反馈的容量大于开环容量,但是随着系统信噪比的增加,情况会逐渐相反。如图3(b)所示,当系统信噪比SNR=4 dB时,反馈信噪比为5 dB的容量是5.2 bit,约等于开环容量;但是在SNR=6 dB时,该容量是6.5 bit,小于此时的开环容量。
总之,无误即时CSI反馈容量高于其他方法;有误统计CSI的反馈容量随着SNRfeed的增加而增加;在低SNR时,相对于开环方式,有误统计CSI反馈的系统更容易产生正容量增益。
4.3 反馈信噪比门限
图4描述了不同系统配置下的反馈信噪比门限SNRTh,该门限按照式(17)求出。考虑了3种天线对配置下的系统,包括2×2,3×3,4×4系统。可以发现,SNRTh随着系统信噪比的增加而增加,在低SNR时门限增加较快,在高SNR时SNRTh增加较为缓慢。在低系统信噪比时,低天线对配置系统的SNRTh比高天线对配置的系统高。例如,对于SNR=4 dB,2×2系统的SNRTh是6.6 dB,高于3×3系统的5.13 dB。但是随着SNR的增加,情况逐渐变的相反。例如,在SNR=12 dB时,2×2,3×3,4×4系统对应的SNRTh分别为12.4,12.6,13.5 dB。总之,该结果给出了若干参数对反馈信噪比门限的影响,对于系统设计有一定参考作用。
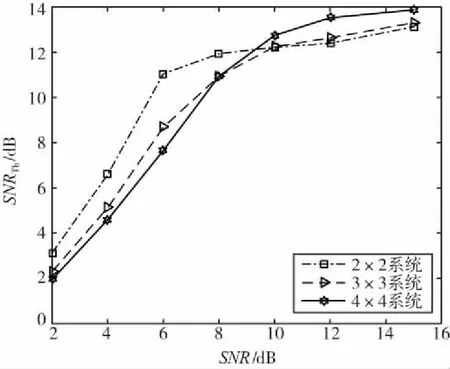
图4 不同系统配置下的反馈信噪比门限
5 结束语
研究了基于统计CSI的闭环MIMO系统容量,分析了反馈信噪比对系统容量的影响,对比了若干典型反馈方式下的系统容量。结果表明,当反馈信噪比门限高于某个值的时候,闭环系统容量相对开环容量才有正增益,在低SNR时,基于有误统计CSI反馈的系统更容易产生正容量增益;反馈信噪比门限随着系统信噪比SNR的增加而增加;在低系统信噪比时,低天线对配置系统的反馈信噪比门限比高天线对配置的系统高,但是在高系统信噪比时,情况相反。研究结果将对MIMO系统的工程实践应用有一定的参考作用。
