一种基于截断高斯先验和变分贝叶斯的多分类算法

田 星，陈欢欢

(中国科学技术大学 计算机科学与技术学院，合肥 230026)

1 引 言

参数模型往往对数据集中样本的分布情况有过强的假设，但真实世界的数据又与这些假设相差甚远，这导致了参数模型对训练集的拟合较差.非参模型无需对训练集样本分布情况进行假设，而是直接通过训练集来估计样本分布情况.核方法[19]能够将每个训练样本转化为一个非线性映射，这些转化为非线性映射的样本被称为基样本.使用了核方法的模型是最为常见的非参模型.非参模型虽能很好地拟合训练集，但也会同时拟合训练集中存在的误差，造成过拟合问题.同时，当训练集很大时，非参模型会导致对应的优化算法的空间和时间消耗都非常巨大.

为了解决非参模型的过拟合问题和参数过多导致算法空间和时间消耗过大的问题，研究者们通过在模型参数上引入先验或通过直接在损失函数中加入正则项等方法，让算法在迭代中自动修剪冗余的参数，实现稀疏的目的.稀疏的非参模型不仅减轻了算法的时间、空间消耗，也一定程度上缓解了对训练集过拟合的问题，提高了模型的泛化能力.稀疏核方法是同时兼具核方法和稀疏特性的一类算法的统称.该类方法在近几十年的分类领域获得了巨大成功和广泛关注.支持向量机(Support Vector Machines，SVMs)[1]、相关向量机(Relevance Vector Machines，RVMs)[2]和概率分类向量机(Probabilistic Classification Vector Machines，PCVMs)[3]均属于其中.

SVMs的优化目标是寻找具有最大间隔的划分超平面，通过核方法的使用，可将SVMs的适用范围从线性可分数据集扩展到线性不可分数据集.然而SVMs的输出不是概率的，而只是+1或-1，在非对称的代价下，概率输出能更好地计算代价[2].RVMs基于贝叶斯框架，通过贝叶斯公式，由先验和似然得到后验，最终通过最大化模型的后验概率，得到权重的极大后验估计.相比SVMs，RVMs能够直接输出测试样本属于正类或负类的概率.Chen等人指出，RVMs的决策可能会基于与样本标签不一致的基样本，这种基样本被称为不可靠的基样本，它导致了RVMs对核参数的异常敏感[3].为解决这一问题，Chen等人提出了PCVMs.PCVMs通过引入截断高斯先验，保证了基样本参数的正负与其标签的一致.相比SVMs，PCVMs基于贝叶斯框架，能够直接输出概率，相比RVMs，PCVMs拥有更合理的先验，模型对核参数的扰动更加稳定.稀疏核方法由于其清晰的解释性和出色的性能，在近几十年受到机器学习领域的广泛关注.但值得注意的是，无论是SVMs、RVMs还是PCVMs，均是在讨论正类和负类的数据，即二分类问题.在二类数据集上表现优异的稀疏核方法，不能直接应用到更广泛的多类数据集上.面对这一现状，很多研究者已经开始了将稀疏核方法中仅支持二分类的算法推广至多分类的研究工作.在文献[4]中，Weston等人将SVMs拓展至多类，提出了多分类支持向量机.同样地，在文献[5]中，Damoulas等人提出了多分类相关向量机.

2 截断高斯分类模型和变分贝叶斯优化算法

2.1 截断高斯多分类模型

我们首先考虑在二类情况下截断高斯先验的使用.稀疏核方法类算法的判别函数是：

f(x,w)=kT(x)w+b

(1)

其中k(·)=[k(·,x1),k(·,x2),…,k(·,xN)]T，是N个由训练样本构成的非线性函数.它将测试样本x映射为一个n维特征向量，wi是模型参数(每个训练样本对应一个模型参数，其中与非零模型参数对应的训练样本称为基样本)，b是偏置项.在RVMs中，wi服从高斯先验，即只约束了它的取值不能过大，而对取值的正负没有任何约束，忽略了样

图1 两种截断高斯分布Fig.1 Two truncated Gaussian distributions

本标签ti提供的信息.而在PCVMs中，当基样本xi属于正类时，wi服从左截断高斯先验，反之服从右截断高斯先验.截断高斯分布是将标准高斯分布N(μ,σ2)的一部分截断，并重新进行归一化，记为Nt(μ,σ2)[3].图1分别展示了两种截断高斯分布的概率密度函数图像.左图是将标准高斯分布的右侧截断，得到的右截断高斯分布，右图是将标准高斯分布的左侧截断，得到的左截断高斯分布.当公式(1)取值大于0时，PCVMs判定该样本属于正类，反之则属于负类.当考虑多类问题时，我们无法使用正类、负类来描述样本，因此该公式无法直接推广至多类问题.这时我们考虑将kT(x)w分为两部分：

∑i:ti=+1wik(x,xi)+∑j:tj=+1wjk(x,xj)

(2)

即将属于正类基样本的求和与负类基样本的求和分开，由于wj服从右截断高斯分布，添加一个负号后，它将与wi一样，服从左截断高斯分布.我们定义：

yc=∑i:ti=cwik(x,xi)+bc

(3)

其中bc为偏置项.我们称yc为x在第c类的势能.此时判别函数可表示为：

f(x,w)=y+1-y-1

(4)

当时y+1>y-1，判定样本属于正类，反之属于负类，即属于势能大的一方.公式(4)便可以推广至多类问题，此时判别函数为：

f(x;w)=argmax(y1,y2，…，yc)

(5)

而多类的概率输出也可由softmax函数直接得到：

(6)

此时在C个类中，任意的基样本对应的权重均服从左截断高斯分布，即：

(7)

其中α是n维向量，分别是wn对应左截断高斯分布的精度参数.在贝叶斯角度下，未知参数α同样被视为随机变量，也需要定义先验.本文采用截断高斯分布精度参数的共轭先验Gamma分布作为α的先验分布，即：

(8)

其中c1，d1是Gamma分布的参数，一般设置为非常小的值，以达到不提供过多信息的目的[2].对于C维偏置向量b，它不会引起不可靠的基样本，所以无需限制它的取值，它的先验分布可选择高斯分布：

(9)

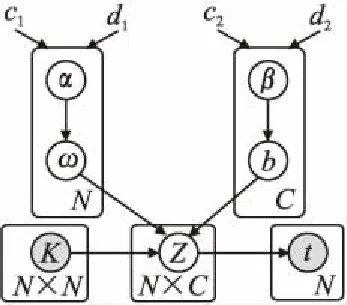
图2 截断高斯多分类模型的概率图模型Fig.2 Probabilistic model of TGMM

同样地，βc是bc的精度参数，服从高斯分布的共轭先验Gamma分布.考虑到势能与数据的真实类别之间存在的误差，我们定义隐变量

zc=yc+ε

(10)

其中ε～N(0,1)，为白噪声.截断高斯多分类模型的概率图模型如图2所示.图中圆盘表示随机变量，点表示固定的常数，阴影表示可被观测的变量，有向箭头表示概率依赖关系.

2.2 截断高斯多分类模型的变分贝叶斯算法

在概率图模型上的贝叶斯推断是指求概率p(θ|X,t)，即给定测试数据集X和标签t，需要推断出参数θ的后验分布.通常使用的算法包括期望最大化(Expectation Maximization，EM)[10]和变分贝叶斯(Variational Bayesian，VB)[6].EM算法将模型中的未知变量分为隐变量和参数两类，并假设隐变量是服从某种分布的随机变量，而认为参数是一个有确定取值的量，不同于随机变量.这种假设被认为是一种非完全的贝叶斯方法[11]，它并不能真正求得参数θ的后验概率，而仅能得到后验概率的峰值(mode).相反，在变分贝叶斯中，参数和隐变量均被视为随机变量，所有的未知量都采用积分或求和的方式消除，能够真正得到参数的后验概率p(θ|X,t).本文将采用变分贝叶斯算法.

变分贝叶斯对后验概率唯一的假设是，它可以被分解为：

(11)

即K个参数的后验相互独立.由此唯一的假设，我们可以得到各分量的最优分布满足如下形式[7]：

(12)

将上述公式结合截断高斯多分类模型，我们有：

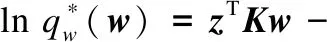
(13)

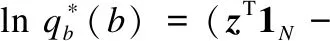
(14)

(15)

(16)

其中K是N×M维核矩阵，δ(·)是集合[x:x>0]的特征函数，即当x>0时，恒为1，其它情况恒为0.在给定N×C维隐变量矩阵Z后，C类之间的概率相互独立，为了简洁，上述公式均忽略了小标c.

由上述ln(·)形式的关系可以得到4个参数对应的分布.分别是：

(17)

(18)

(19)

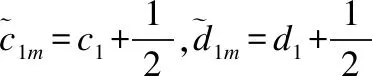
(20)

注意到变分贝叶斯并没有假设q*(·)的具体形式，但我们对参数使用共轭先验后，推导得到的后验与先验有相同的函数形式.即w的后验分布仍是左截断高斯分布，b的后验分布仍是高斯分布，而α和β的后验分布仍是Gamma分布，他们的区别仅是分布的参数不同.

在最优形式q*(·)中需要使用的统计量计算如下：

(21)

(22)

(23)

(24)

Ewi[wi]=2N(0|0,1)

(25)

(26)

可以看出，在给定Z后，为了求得后验的最优形式q*(·)，我们需要的统计量即式(21)-(26)，而在计算这些统计量时，需要最优形式的参数，即式(17)-(20).所以变分算法的迭代形式是：初始化所有参数，先由式(21)-(26) 更新统计量，再由式(17)-(20) 更新最优分布的参数，如此交替，直至收敛算法为止.变分算法的收敛性证明可参阅文献[9].最后，我们给出在变分算法收敛后，隐变量Z的更新公式，当e≠tn，c=tn时：

(27)

(28)

其中ε～N(0,1).VBTGMM算法首先对所有变量进行初始化，然后固定Z，通过变分算法计算b和w，之后利用公式(27)和公式(28)，更新Z，同样是交替进行，直至满足收敛条件.

2.3 模型算法总结与分析

3 实验结果与分析

为了验证VBTGMM的有效性，我们设计了三组实验.首先我们在一个人工合成的不平衡二维数据集上进行测试，以图的形式直观展示VBTGMM的特点.之后我们将在8个来自UCI的数据集上进行实验，验证VBTGMM在真实世界数据集的表现.从章节(2.3)的理论分析可知，VBTGMM在数据集的类别数较大时，会明显优于其它多类算法，因此我们设计了一个让训练集类别数逐渐增加的实验，用以验证理论分析.

本节使用的对比算法有：两个多类版本RVMs算法：增量形式的mRVM1和基于期望最大化的mRVM2[12]；多类版本的SVMs，来自LIBSVM软件包的实现[13]；多类版本的逻辑斯特回归算法：多项逻辑斯特回归(Multinomial logistic regression，MLR)；使用最二乘回归构建多类模型的最小二乘回归判别(Discriminative Least Squares Regression，DLSR)[14]；能够自动修剪冗余神经元并使用耦合方法构建多类的稀疏贝叶斯超限学习机(Sparse Bayesian Extreme Learning Machines，SBELM)[15].

3.1 人工合成数据集实验

该数据集是由10种不同颜色的二维向量构成，每类点围绕在一个区域，相互直接没有重叠的地方，原始的数据在二维平面上的分布如图3左上所示.总共132个样本，我们从左至右，从上至下，分别称类别为第1类，第2类，…，第10类，例如灰色点是9类.不同类之间分布不平衡，小类例如第6类仅有5个样本，大类例如第1类有19个样本.由于mRVM1和mRVM2与VBTGMM有相似之处，本次实验中，我们将使用这两个算法作为对比.三个算法均使用径向基核函数(Radial Basis Function，RBF)[16]，且采用相同的核半径参数.

实验结果如图3的后三幅图所示.图中不同颜色表示3个分类器划分出来的区域.可以看到，VBTGMM完美地用曲线分割了10个区域，包括小类(第4类和第6类).

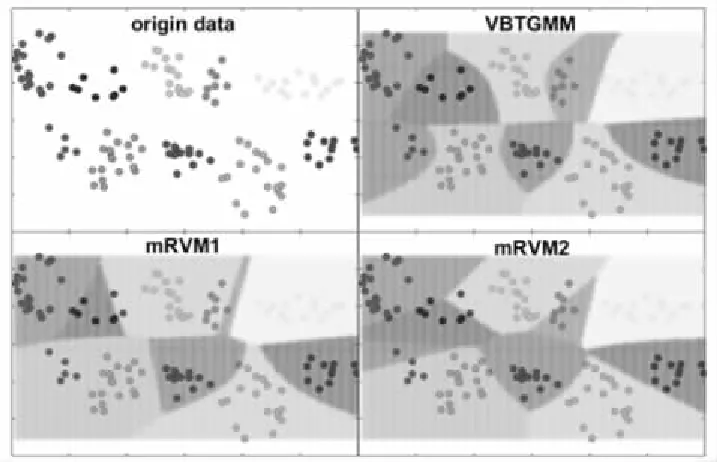
图3 在人工合成数据集上三个算法:VBTGMM,mRVM1和mRVM2的表现Fig.3 Performance of the three algorithms:VBTGMM,mRVM1,and mRVM2 on the synthetic datasets

而mRVM1则完全忽略了第6类，将所有的第6类点划入了第7类.同样第4类的大部分点都被划入了第3类中.mRVM2的情况稍好于mRVM1，但它在第2类，第4类，第6类的划分上，都不同程度地倾向于忽略小类.对于mRVM2，注意到它的类间边界非常“线性”，由于三个算法都使用了RBF核函数，分界线一般情况下理应是二次曲线的叠加.为了能构成直线的边界，只能是拥有众多未被修剪(权重不为零)的基样本.

表1 mRVM1，MRVM2和VBTGMM在人工合成数据集的10类上各自的基样本个数Table 1 Number of base samples of mRVM1,mRVM2,and VBTGMM in each of 10 classes of the synthetic data

这一猜测可以被表1验证.表1记录了三个算法在10类的基样本个数.我们可以看到，mRVM1和mRVM2均在第4类没有基样本，正因为如此，它们在分类时完全忽略第4类的样本.mRVM1和mRVM2分别拥有25个和15个基样本，VBTGMM拥有16个基样本，它们似乎拥有接近的稀疏效果.然而如果考虑基样本对应的非零权重个数，VBTGMM每个基样本只对它所在的类的权重有贡献，所以每一个基样本恰对应一个权重，权重个数与类别数无关.但mRVM1和mRVM2不同，它们的每个基样本都有C个权重，在本次实验中，C=10，即每个基样本提供10个不同的权重.所以mRVM1和mRVM2分别拥有250个和150个非零权重，而VBTGMM仅拥有16个非零权重.过多的非零权重也使得mRVM2通过大量二次曲线的叠加，得到了“线性”的分界线.

3.2 8个UCI数据集实验

在本节中，我们将使用8个来自UCI的公开数据集，通过VBTGMM与其它6个对比算法的对比，验证它的有效性.数据集的详细信息和划分比例见表2.

由于在真实世界中，数据集常常是不平衡的，即各类样本数量差距很大，这在多类数据集中尤为明显，此时不适合仅用错误率评价算法优劣.因此，本文选取的评价指标不仅包括错误率，也包括ROC(Receiver Operating Characteristic)曲线下面积AUC(Area Under Curve).由于AUC仅支持二类数据，我们实际采用文献[17]对它的推广形式.遵循文献[18]中的实验方法，我们将数据集随机划分为训练集和测试集50次，使用前5次划分进行参数选择.得到5组最优参数后，选取它们的中位数作为后45次划分的参数.分别使用之后的45次随机划分的训练集和测试集进行训练和测试，得到45组错误率和AUC值.

表2 8个来自UCI的公开数据集详细信息Table 2 Details of eight public datasets from UCI

表3是45次实验的错误率和AUC值的平均值(和标准差).一些算法在一些数据集上无法在可容忍时间内运行出结果，我们用(Time Limit Exceeded，TLE)标记.8个数据集是以类别数排序，类别数从左至右逐渐增大.可以看出，当类别数较小时(比如4或6)，各种算法区别不大.但当类别数增大时，VBTGMM在错误率和AUC两个指标下均有优秀表现.注意到同为基于贝叶斯的算法，mRVM1和mRVM2在训练集变大时，便无法在可接受的时间内运行结束.而正如之前的理论分析，由于VBTGMM将矩阵求逆时基样本数从降至平均的，拥有相对较小的时间消耗.值得一提的是，当数据集的类别数达到100时，4个对比算法都无法在合理时间内运行出结果，而剩下2个对比算法在也错误率和AUC上，与VBTGMM相差甚远.能在100类这种大类别上达到一个比较理想的结果，得益于在TGMM中，权重在初始时是一个的向量.而同类算法的权重是一个会随类别数增加而增加的矩阵.更多的权重带来的过拟合导致它们在测试集上的表现不佳.

表3 VBTGMM和6个对比算法在8个公开数据集上的45次随机划分实验的错误率和AUC值的平均值(标准差)Table 3 Error rate and AUC (standard deviation) of VBTGMM and other 6 baseline algorithms of 45 randomly-split experiments on 8 public datasets

3.3 不同类别数下各算法的表现

通过上文的理论分析和实验，我们注意到当类别数较大时，VBTGMM拥有很大优势.本节我们将设计实验进一步观察和验证这一点.同样我们选取UCI上的数据集字母识别(Letter Recognition).该数据集拥有26类，分别代表26个英文字母.我们选取其中的前10类，即′A′-′J′.首先使用600个′A′类数据和600个′B′类数据，组成2类数据集，之后逐渐增加600个′C′，600个′D′，…，直至′J′.得到2-10类，9个类别不同的数据集.在这9个类别不同的数据集中，每个对比算法均在随机划分下训练和测试10次，得到精度的平均值.由于该数据集是平衡的，无需额外记录AUC值.实验结果如图4所示.从图4中可以看到，当数据集只有2类时，7个算法拥有基本相同的结果，随着类别数的增加，分类问题的困难程度也在增加，各个算法的精度也随之下降.但下降趋势各不相同，在对比算法的精度急剧下降时，VBTGMM逐渐成为了第一名.通过本次实验，可以确信VBTGMM在类别数较大时优于本文的6个对比算法.

图4 数据集的类别数增加时算法分类精度变化图Fig. 4 Curves of classification accuracy rate changing with the number of classes

4 结论与展望

本文基于贝叶斯框架，提出了基于截断高斯先验的多分类模型TGMM.截断高斯的使用，不仅解决了高斯先验忽略标签信息，带来不可靠基样本的问题，也使得模型参数不会随类别数增加而增加，降低了求解算法的复杂度，缓解了矩阵求逆时精度导致的结果不稳定问题.基于TGMM，提出了VBTGMM算法，它是基于变分贝叶斯的优化算法，对权重向量和隐变量的分而治之，使得即便是不平衡中的小类，也不会被忽略.在人工合成数据集和来自UCI的真实世界数据集上，均验证了上述理论分析，尤其是当类别数较大时，实验结果明显优于同类的对比算法.