皮托管式静压探针气动性能的CFD和试验对比研究

2019-05-05刘绪鹏刘忠奎田吉祥李宏宇刘国阳

航空发动机 2019年2期

刘绪鹏，刘忠奎，田吉祥，李宏宇，刘国阳

（中国航发沈阳发动机研究所，沈阳110015）

0 引言

航空发动机内流场的静压是评估其性能的重要参数。用于发动机内流场静压测试的探针需要满足尺寸小、可靠性高、精度高、测点多的要求。因此，1支静压探针通常需要布置多个测点，以捕捉静压的分布情况。要在诸多的限制条件下设计出1种合格的静压探针难度很大。学者们在静压探针的结构设计和气动性能方面做了大量工作。在结构设计方面，刘笃喜等[1-2]通过数值计算发现，静压探头的长度和感压孔直径是影响精度最主要的2个因素，并分析了感压孔尺寸对测试精度的影响；孙志强等[3-4]通过试验和数值仿真对比，分析了静压探针支杆和安装角度对测试结果的影响，以及静压探头的尺寸对测试精度的影响；杨欢等[5]通过CFD和试验方法，分析了探头形状对皮托管性能的影响；祖孝勇等[6]在用于冰风洞风速测量的皮托管设计中，通过仿真分析得到较优的测压孔开孔方案；Shmueli等[7]通过试验和CFD方法研究了1种可用于气液混合流场测试的皮托管，并对其结构进行了改进；Rex[8]介绍了3种用于气流速度测量的皮托管结构。在气动性能方面，Boleslaw等[9]通过CFD方法研究了1种自平均皮托管的气动性能；Zagarola[10]研究了外径直径分别为 0.30、0.51、0.90、1.83 mm 的皮托管的性能；Masud[11]利用皮托管上、下表面静压分布特性，在此基础上设计了1种飞机攻角测量探针；Wysocki等[12]通过试验研究了皮托管测试的修正方法；Lighthill[13]分析了造成皮托管偏移效应的机理。

皮托管式静压探针结构简单，可以在1支探针上布置多个测点；测试结果规律性较强，易于修正；几何外形小，测试可靠性高，对发动机的测试改装要求低。在航空发动机的静压测试工作中应用广泛。本文通过CFD计算和试验验证，研究了皮托管式静压探针的气动性能，并据此给出较优的设计方案。

1 皮托管式静压探针测压原理

皮托管式静压探针（以下称“静压探针”）的结构如图1所示。图中:x1表示静压孔距探头端部距离；x2表示静压孔距支杆距离；d1表示探头直径；d2表示支杆直径。在静压探针工作时，气流首先冲击探头前端，在探头的滞止作用下压力达到最高，数值上等于气流的总压；然后气流流过探头前端，速度增加，静压降低，使得此处压力降低；当气流到达支杆附近，由于滞止作用，速度降低，压力再次升高。

图1 静压管结构

图2 探头前端与支杆对静压测量的影响[14]

探头前端和支杆对静压测量精度的影响如图2所示。从图中可见，随着测压孔远离探头前端和支杆，压力系数减小，即静压值更接近真实值。静压探针的设计原则就是选择合适的测压孔位置，尽量使探头端部和支杆造成的误差相互抵消。例如，图2示出的静压探针的气动特性，当x1=3 d1，x2=8 d2，前端对静压孔造成-1.1%的误差，而支杆带来1.1%误差，二者恰好抵消，即气动误差被消除。

根据上述原理，本文研究了专门用于航空发动机内流场静压测量探针的气动性能。对该种静压探针具有以下限制条件:尺寸小，通常静压探针的安装孔的直径不大于20 mm，这也限制了探针的整体尺寸；支杆粗，为了增加静压探针的强度储备，支杆的直径需要不小于8 mm。由于受上述因素的限制，静压探针的测量结果通常具有较大的偏差，需要通过风洞试验得到的校准曲线对测量结果进行修正。

2 CFD计算及分析

2.1 流场模型和主要气动参数

静压探针CFD模拟的流场模型如图3所示。图中，d1=1 mm，d2=8 mm。流场的进口距探针75 mm（约9 d2），流场出口距探针 222 mm（约 28 d2），流场进口宽240 mm（30 d2）。由于探针所处的流场对称，为简化计算仅对流场的一半建模。

图3 P2432探针CFD计算3维流场模型

流场参数选取当地的大气参数，大气压力为101.0 kPa，大气温度为273 K。

2.2 网格无关性分析

网格的质量对CFD计算结果的准确性有较大影响。原则上网格质量越高，数量越多，计算精度越高，但过多的网格又会导致对计算资源的需求大幅上升，而低密度网格虽然计算速度快，但是精度却难以保证。因此在开展CFD气动性能分析之前，采用探头表面的压力系数Cp分布情况作为判断的指标，开展网格无关性研究

式中:P为当地压力；Ps为来流静压为来流动压。

采用当地的大气参数作为流场的基本边界条件，气流速度取Ma=0.4，湍流方程采用k-epsilon，计算精度为High Resolution。在商用软件CFX中进行仿真计算，探头的压力系数分布如图4所示，不同的网格密度的分析结果见表1。

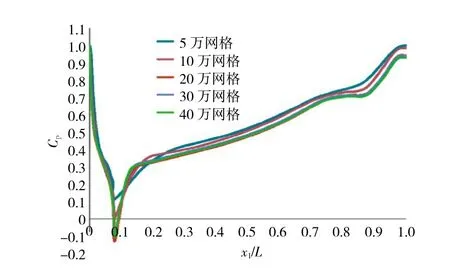
图4 不同网格密度下探头的压力系数分布

表1 不同密度的网格对比

通过不同网格密度计算结果的对比发现，网格密度为5万和10万时，其压力系数曲线与其他高密度网格曲线有明显偏离，而且没有捕捉到探头上的负压区域；在网格密度达到20万时，压力系数曲线虽然在绝大部分区域与高密度网格有较高的重合度，但是在约x1/L=0.08附近，则有明显偏离；在网格密度达到30万以上后，压力系数曲线随着网格数量的增加已经无明显变化，说明随着网格密度的增加计算结果的精度并无显著提高。因此，在CFD计算中采用30万的网格密度，网格的详情如图5所示。

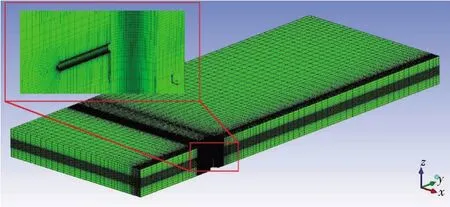
图5 CFD计算采用的网格

2.3 CFD计算结果及分析

CFD计算仍采用CFX软件，计算的网格和边界条件设置见表2。

在不同Ma下，静压探针的压力分布如图6所示。从图中可见，探头在Ma=0.3～0.7的范围内有着相同的压力分布规律。在探头的前端由于气流被滞止，此处压力最高；随着气流流过探头前端，型面的变化对气流产生加速作用，压力降低；随后在支杆对气流的滞止作用下，压力回升，随着气流流向支杆的方向，压力逐渐增加，直到到达支杆处，气流又一次被滞止，压力再达到高点。在圆柱支杆部分，气流流过支杆前缘后，在绕流支杆的过程中加速，导致压力明显下降，直至到附面层的分离点附近，压力回升。随着气流速度的增加，附面层分离点明显前移。

表2 CFD计算的边界条件

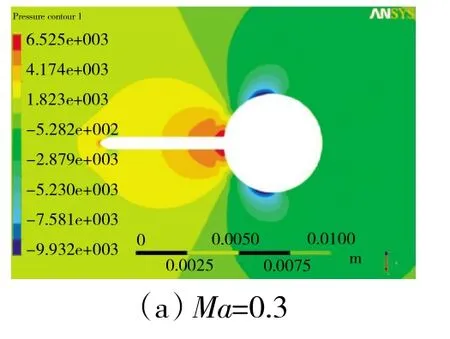
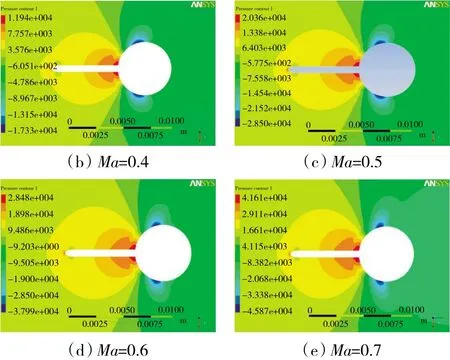
图6 不同Ma下探针压力分布

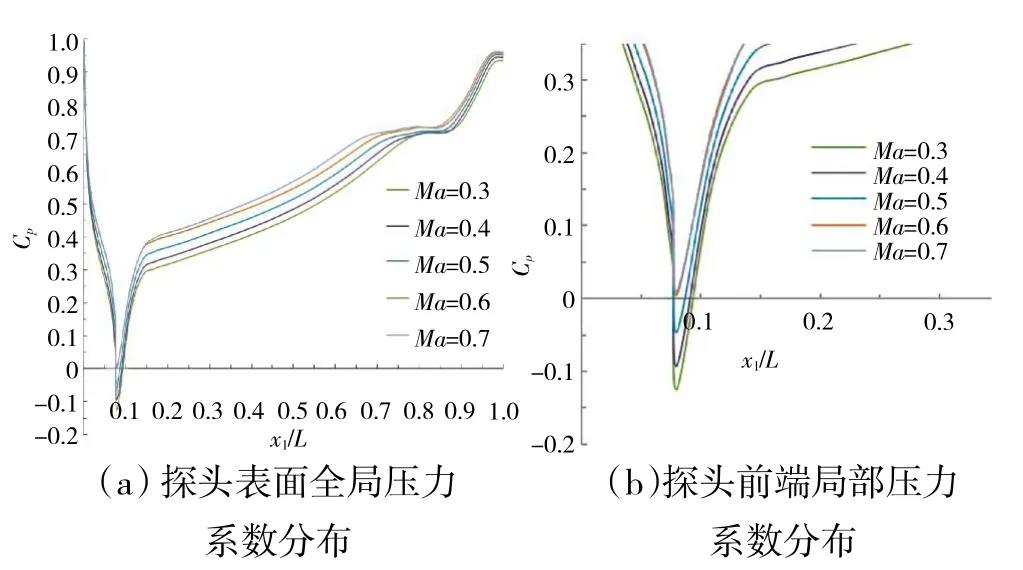
图7 探头表面压力系数分布曲线

探头表面的压力系数分布如图7所示。从图中可见，压力系数的分布与图6的结果吻合。在探头前端附近压力系数从1开始呈急剧下降趋势，直到在约x1/L=0.07附近出现最低值；随后压力系数迅速升高，在约x1/L=0.15处，其升高趋势放缓；直至探头与支杆连接处接近1。在不大于Ma=0.5的情况下，探头上至少有2个点的压力系数为0（位于约x1/L=0.07和x1/L=0.09附近），也就是说探针气动特性造成的系统误差为0。但是在x1/L=0.05～0.07范围内，曲线的斜率急剧下降，因此在较低Ma下不建议在此范围内开测压孔；在x1/L=0.08～0.10范围内，曲线斜率的变化趋势相对较慢，在低Ma下在此范围内开测压孔会取得较好的效果。在Ma=0.6、0.7时，探头在约x1/L=0.07处压力系数最小，即系统误差最小。根据静压探头的上述特点，以及被测流场的特点，在x1/L=0.07～0.10范围内开测压孔会测得较高的精度。

通过对比试验发现，随着Ma的提高，探头表面的压力系数整体上呈现出升高的趋势，即静压相对动压端的比例上升。其原因是由于随着Ma升高，支杆两侧的附面层分离点前移，使得支杆造成的堵塞面积增加，对气流的滞止作用加强，导致探头表面的压力升高。进口气流速度Ma=0.3、0.7时探针附近气流的Ma对比如图8所示。从图中可见，在Ma=0.7时，探针的支杆局部出现了超声速区域并引起附面层分离，分离点比Ma=0.3时显著提前。

图8 在Ma=0.3、0.7时探针附近流场的Ma对比

总之，CFD计算结果显示，在约x1/L=0.07～0.10范围内开测压孔，会得到较高的测试精度。在Ma=0.3～0.7的范围内，静压探头上的压力系数有相同的分布规律，并随着Ma的升高而略有增大。。

3 风洞校准试验

3.1 试验探针介绍

试验使用的探针结构如图9所示。为了研究探头表面的压力分布情况，在直径为8 mm的探针上布置5个长10 mm的探头，在每个探头上距离前端分别9、7、5、3和1 mm的距离开直径为0.3 mm的测压孔，编号分别为1～5。探针实物如图10所示。

图9 静压探针试验件结构和测压孔

图10 试验用探针实物（局部）

3.2 试验结果和分析

本次试验在某型亚声速校准风洞中完成，当地环境温度约为273 K，大气压力约为100950 Pa。气流的攻角为0°，试验状态点为Ma=0.3～0.7，步距Ma=0.1。试验件为3支结构相同的静压探针，编号分别为:P2432-950、P2432-951和P2432-952。试验测得3支静压探针的压力系数见3～5，表中下标1～5为测压孔编号。

表3 P2432-950在各Ma下的压力系数

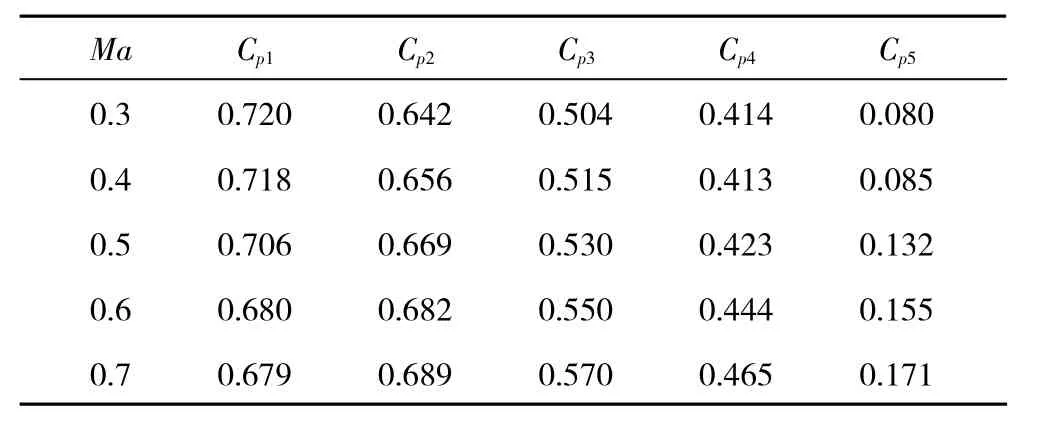
表4 P2432-951在各Ma下的压力系数

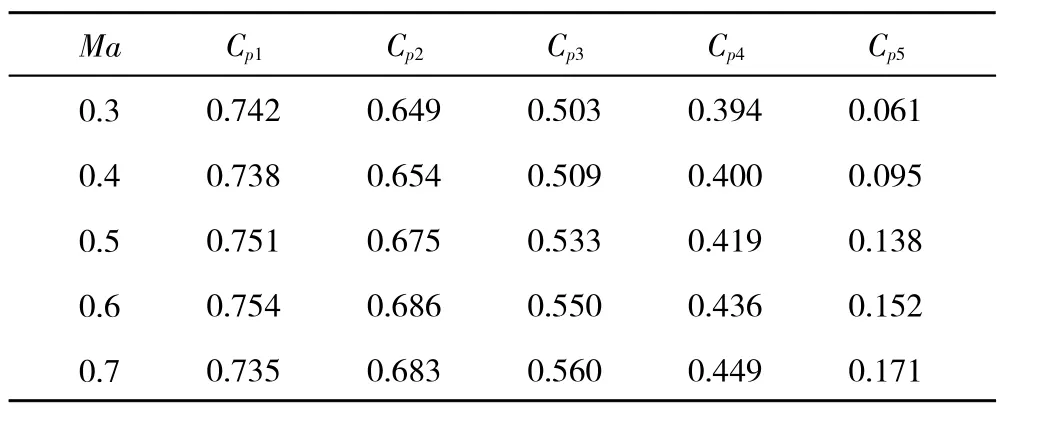
表5 P2432-952在各Ma下的压力系数

3支探针在不同Ma下，静压探头的压力系数分布规律如图11～13所示。从图中可见:

（1）3支探针在不同Ma下各测点压力分布规律相同，从孔5～1压力系数都呈现逐渐增大的趋势，符合CFD计算结果。

（2）在不同Ma下，各孔的压力系数整体上随Ma的增加而增大，这一结果也符合CFD模拟结果。

（3）在不同Ma下，在x1/L=0.1测点测得压力系数最小，也就是说相对其它测点测得的静压值最接近真实值，这也与CFD计算结果相符合。

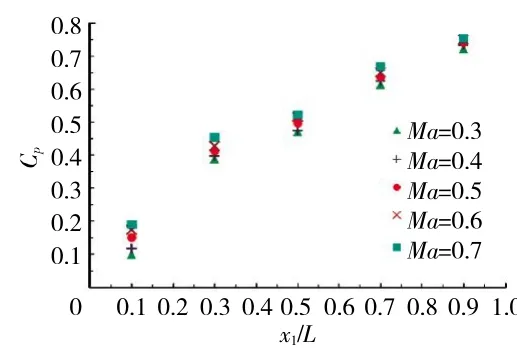
图11 P2432-950探针在不同Ma下探头压力系数分布

图12 P2432-951探针在不同Ma下探头压力系数分布

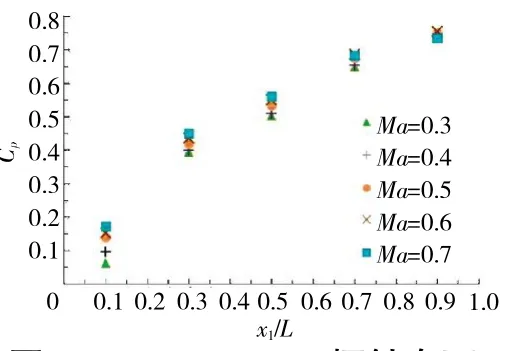
图13 P2432-952探针在不同Ma下探头压力系数分布

3.3 测试精度分析

在静压探针的应用中，1个最重要的指标就是静压测试误差E，直接决定了静压测试结果的准确程度

式中:Ps_probe为探针测得静压；Ps为来流静压。

通常为了达到试验需求的精度指标，在静压探针使用前需要进行风洞校准试验，以便获得探针的校准曲线。再通过校准曲线对静压测量的结果进行修正。

根据试验结果计算的各测压孔的误差见表6～8。从表中可见，在不同Ma下，从1～5号测压孔的误差递减；同一测压孔的误差随着Ma的减小而减小，这种趋势与CFD计算结果一致。值得注意的是，在发动机测试中一般对静压探针的误差要求为不大于1%，而第5孔的误差在Ma=0.3时远低于1%；在Ma=0.4时接近1%。也就是说，当被测气流的速度在Ma=0.3左右时，由5号测压孔测得的静压值不经修正即可满足使用要求。因此，在部分低Ma试验状态下，采用5号测压孔的设计方案，能够节省探针风洞校准试验的成本和缩短试验周期。

表6 P2432-950探针各测点在不同Ma下的误差 %

表7 P2432-951探针各测点在不同Ma下的误差 %

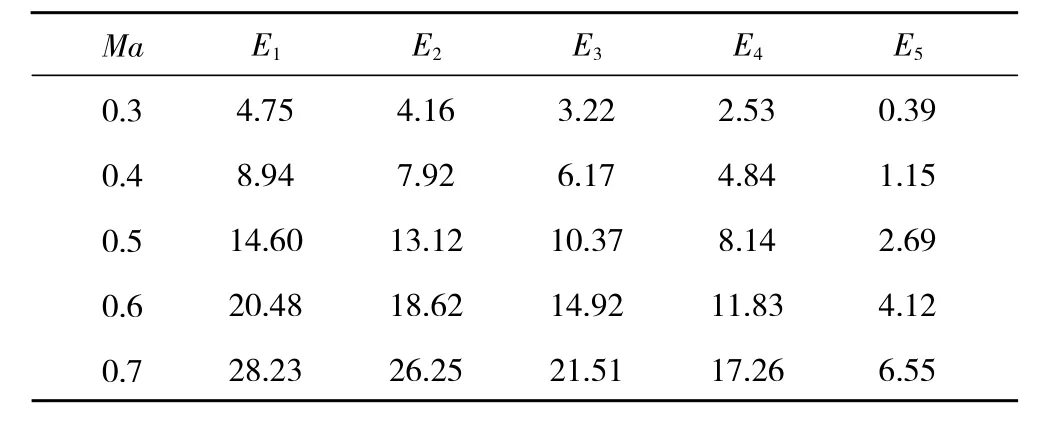
表8 P2432-952探针各测点在不同Ma下的误差 %

4 试验与CFD计算结果对比

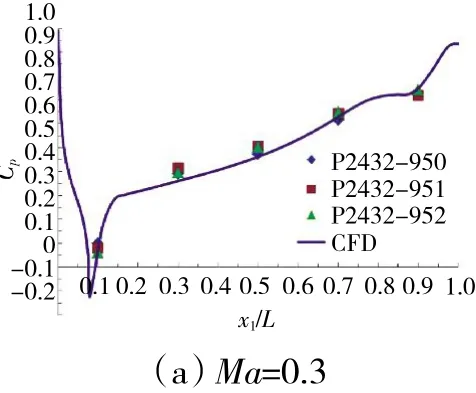
图14 不同Ma下探头表面压力系数试验和CFD计算结果对比

3支静压探针在不同Ma下的试验结果与CFD计算结果的对比如图14所示。从图中可见，在不同 Ma下，x1/L=0.1处压力系数的试验数据与CFD计算结果均有较高的重合度。从图14（a）中可见，在Ma=0.3时，x1/L=0.3处CFD计算结果与试验数据有小幅偏离，而在其余测点均有较高重合度；从图14（b）中可见，在Ma=0.4时，所有测点的试验数据都与CFD计算结果有较高的重合度；从图 14（c）、（d）、（e）中可见，除x1/L=0.9测点有部分偏离外，其他测点的试验数据与CFD计算结果都有较高的重合度。综上所述，在不同Ma时，x1/L=0.1处，CFD计算结果与试验结果有很高的重合度，在Ma=0.3～0.7时，x1/L=0.1～0.9的范围内，CFD计算结果也都与试验结果有着较高的一致性。