泰勒公式的应用探究

舒孝珍

(成都师范学院数学学院,四川 成都 611130)

1 泰勒公式[1]

设函数f(x)在含有x0的开区间(a,b)内具有直到(n+1)的导数,则当x∈(a,b)时,f(x)可以表示为(x-x0)的一个n次多项式与一个余项Rn(x)之和:

2 泰勒公式的应用

2.1 利用泰勒公式计算有理函数的不定积分[2]

求有理函数的不定积分,常用的方法是将有理函数通过待定系数法或赋值法分解为最简分式的和的形式求不定积分,这个分解的过程有时候比较麻烦。对于有些求不定积分的题型,若采取泰勒公式,将简化解题过程。

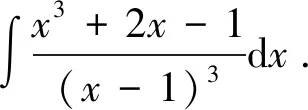
解令f(x)=x3+2x-1,利用泰勒公式将f(x)在x=1处展开,

2.2 利用泰勒公式判断反常积分的敛散性

在判断反常积分的敛散性时,可以先利用泰勒公式对被积函数进行化简后再判别其敛散性。

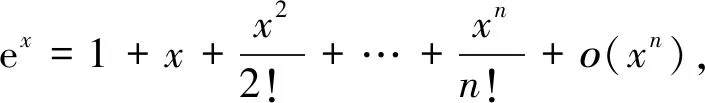
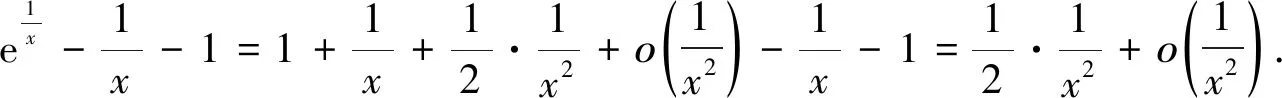
还可以利用泰勒公式讨论某些正项级数的敛散性[4].

2.3 利用泰勒公式证明不等式

在证明不等式时,我们可以利用拉格朗日中值定理、函数的凹凸性、单调性等方法,同时,泰勒公式也是证明不等式的一种重要方法。

例3[5]设f(x)在[0,1]上具有二阶导数,且[0,1]上成立|f(x)|≤A,|f″(x)|≤B.

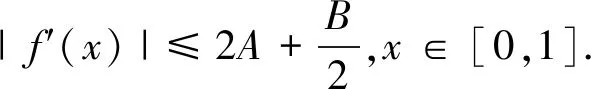
证明∀c∈[0,1],f(x)在x=c处的带拉格朗日余项的泰勒公式为:

其中ξ在c与x之间,因此ξ∈[0,1].特别地

其中ξ1,ξ2∈[0,1].将以上两式相减得

由已知条件可得

2.4 利用泰勒公式确定某些函数的原函数

有些函数的原函数是非初等函数,一般不容易找到,可以采用泰勒公式的幂级数展开式来找到它的原函数。

例4 求函数f(x)=arctanx,x∈(-1,1)的原函数.

解当x∈(-1,1)时,由泰勒公式可得

由于f(x)在x∈(-1,1)内一致收敛,所以∀x∈(-1,1),f(x)的原函数

2.5 利用泰勒公式求极限

在求极限的问题中,对于用洛必达法则和等价无穷小替换失效的极限问题,一般可利用泰勒公式得到解决。

解将分子与分母中各项分别用带有佩亚诺余项的三阶麦克劳林公式表示,即

因此,

在求曲线的渐近线时,我们也可以利用泰勒公式。

渐近线定义:若曲线y=f(x)上的点(x,f(x))到直线y=ax+b的距离在x→+∞或x→-∞时趋于零,则称直线y=ax+b是曲线的一条渐近线。

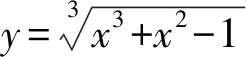
渐近线方程中,通过泰勒公式求函数极限得到常数b更加简便。

2.6 利用泰勒公式求近似值

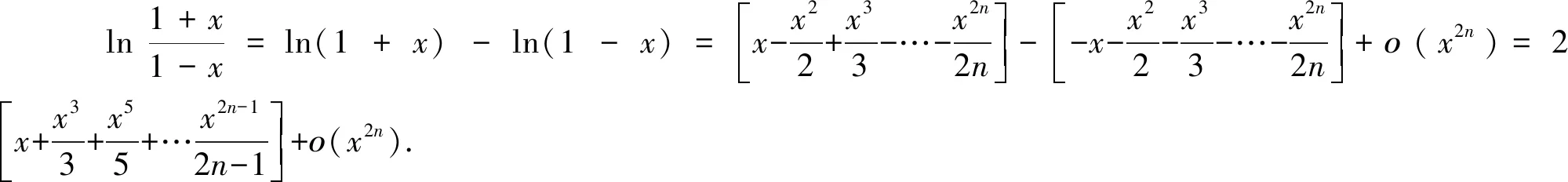
与精确值ln2=0.69314718…的误差小于0.0001.

3 结语

文章从六个方面探究了泰勒公式在分析和研究数学问题等方面的应用,深入探讨泰勒公式的应用,对于解决一些复杂的数学问题可以起到事半功倍的效果。在具体应用泰勒公式时,要具体问题具体分析,灵活应用泰勒公式。