J-NTP对偶泛函的升阶算法

唐桂林

(安徽邮电职业技术学院,安徽 合肥 230031)

对偶泛函在计算机辅助几何设计、图形图像处理中有着重要的作用,利用对偶泛函可以实现各种不同基函数的相互转换,一直以来对偶泛函及其升阶算法的研究受到众多学者的关注。文献[1-8]讨论了不同基函数的对偶基及其应用;文献[9]讨论了一般多项式基函数的对偶基问题;文献[10]给出了泛函分析中对偶基的构造方法;文献[11]给出了J-NTP表达式。由于关于J-NTP基函数的对偶泛函及其升阶算法的相关结果还没有出现，这里首先根据对偶泛函的传统算法,给出J-NTP基函数对偶泛函的升阶算法,并以具体案列来验证所给算法的正确性。

1 J-NTP曲线

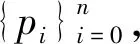
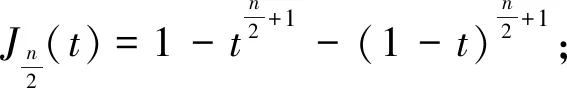
图1 五次J-NTP曲线Fig.1 The five J-NTP curve

2 J-NTP基函数的对偶泛函

定理1 在区间[0,1]上n=2m次J-NTP基函数的对偶泛函可表示为:

(2)

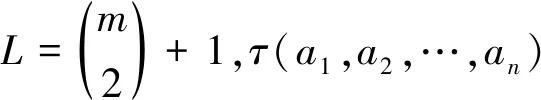
3 J-NTP对偶泛函的升阶算法

引理1j0,j1,…,jn是一组线性无关的基函数,其生成空间为Jn=span {j0,j1,…,jn}则有

(3)

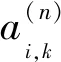
引理2 设p0,p1,…,pn是一组线性正交基函数,其生成空间为Pn=span {p0,p1,…,pn},则有

即

(4)

(5)

下面介绍一种新的升阶算法。该种算法相对于引理1和引理2来说,计算量要少很多。

定理2 设j0,j1,…,jm,m∈{0,1,2,…,n}是m维线性空间的基函数,其生成空间为

i∈{0,1,…,m},j∈{0,1,…,m}

(6)

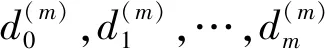
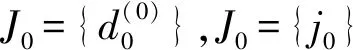
下面构造n+1维欧式空间Dn+1,即有

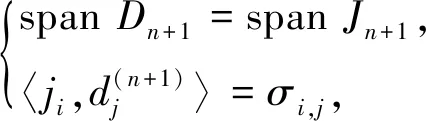
i∈{0,1,…,n+1},j∈{0,1,…,n+1}

(7)

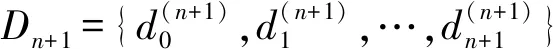
spanDn+1=spanJn+1=spanJn∪{jn+1}=spanDn∪{jn+1}=span {Dn,jn+1}

即有

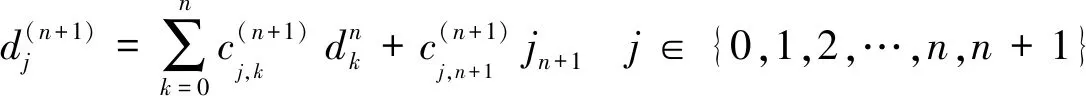
(8)

根据对偶基的定义,则有

当i∈{0,1,2,…,n}时

当i=n+1时

即

其中

4 案例

下面我们以J-NTP基函数为例来验证上述算法。不妨设:

J4={j0,j1,j2,j3,j4},

j0=(1-t)4,j1=t(1-t)3,j2=1-t3-(1-t)3,j3=t3(1-t),j4=t4

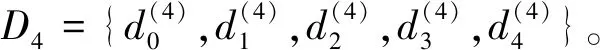
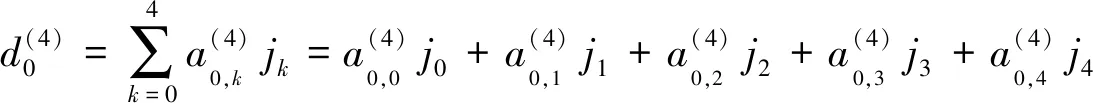
(9)

(10)

1)当i=0时

根据泛函分析中的对偶泛函理论,对下标j进行分类讨论,则有

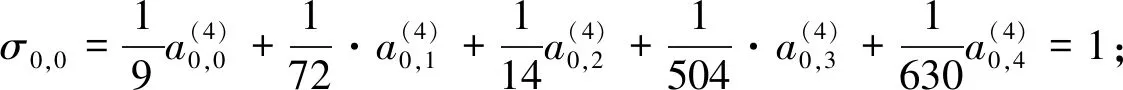
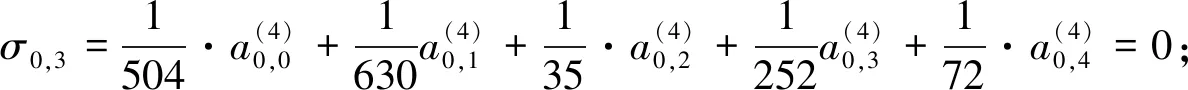
即有

2)当i=1时,同理可有

3)当i=2时,同理可有

4)当i=3时,同理可有

5)当i=4时,同理可有

根据上述算法,我们现在利用4次J-NTP基函数的对偶基来构造5次J-NTP基函数的对偶基函数

(11)

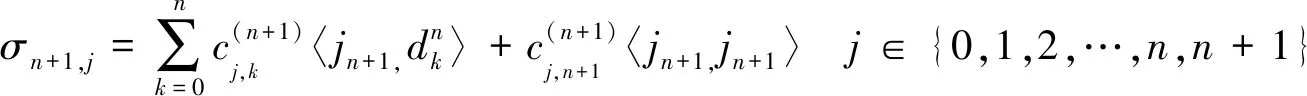
(12)

当j=0时,分别讨论i=0,1,2,3,4,5时的情况:

1)当i=0时,即

2)当i=1时,即

3)当i=2时,即

4)当i=3时,即

5)当i=4时,即

6)当i=5时,即

即有

其中系数矩阵:

当j=0时,可以得到矩阵M如下:

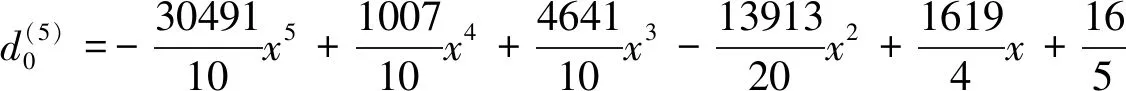
5 小结

根据泛函分析中对偶理论,给出J-NTP 基函数对偶泛函的升阶算法。文中以4次J-NTP 基函数对偶泛函为例，得到5次J-NTP 基函数对偶泛函，验证该算法的正确性。该方法需要解一个线性方程组才能得到对偶基，但与现有的方法相比其解方程组的计算量由O(N3)变为O(N),这在计算机辅助几何设计中有着潜在的应用价值。