基于Abaqus 的等边三角形网格加筋壳建模分析方法及试验验证研究

乐 晨，曹 昱，杨 帆，董曼红，郭 雷

（北京宇航系统工程研究所，北京，100076）

0 引言

等边三角形网格加筋壳是美国宇航局（NASA）20世纪70年代研究出的一种薄壁结构形式。根据文献[1]，这种结构虽然在几何上不完全对称，但在力学性能上具有各向同性、比刚度高的特点，适用于承受均匀压力和轴压载荷的壳段。等边三角形网格加筋壳最初使用化铣加工，随着机械加工能力的增强，机铣逐渐替代化铣，几何精确度大幅提高。它和正交网格加筋壳广泛应用在国外型号上，包括美国大力神V、德尔塔Ⅳ、日本H-2A等。随着加工能力提高，呈逐渐扩大使用范围的趋势，包括美国最新太空发射系统（Space Launch System,SLS）火箭和SpaceX火箭。国外应用这种网格加筋壳制造时，一般都采用3～4块壁板组合成单个壳段。若整壳段较长，则将多个单壳段焊接或组装在一起。

在中国，斜置正交网格加筋壳首先被用于壳段设计。为进一步减重，在新型中型运载火箭上[2]，首次使用等边三角形网格加筋结构进行壳段设计。范瑞祥等人总结了具体结构设计的研究情况，包括工程算法、有限元分析和两个尺度单壳段轴压破坏试验[3]。在研究中，他们使用美国MSC公司NASTRAN软件，建立等边三角形网格加筋壳段模型，开展有限元分析，并与轴压试验结果对比。结果表明：工程算法、线性屈曲计算结果修正后与试验结果相符，但没有给出修正系数；非线性屈曲计算结果与试验结果接近，但实际较小尺度壳段的计算结果高于试验结果20%，较大尺度壳段计算结果高于试验结果6%，未明确计算偏高的误差原因。

对于网格加筋壳结构，试验和计算的误差源来自两方面：

a）来自有限元建模分析方法误差。多年以来，业内公认NASTRAN软件适用于线性有限元分析。而对于网格加筋壳轴压稳定性问题，由于存在强非线性，包括几何大变形和材料弹塑性，达索公司的分析软件Abaqus更为擅长，求解精度更好。

b）壳段自身的初始几何缺陷对承载能力的影响不容忽视。这种缺陷源自制造、运输、装配等诸多环节，最终造成承载能力降低。NASA兰利研究中心（Langley Research Center，LRC）自2000年以来研究网格加筋壳制造缺陷敏感性对轴压承载能力的影响[4,5]。研究人员使用光测技术对制造后的壳段进行测量，获取实测点阵数据后，将几何缺陷引入理想有限元模型，重新计算后，试验和计算符合良好。大连理工大学的郝鹏、王博等人对网格加筋壳的几何缺陷敏感性也开展了大量研究，包括基于缺陷的轴压承载能力可靠性优化等一系列工作[6～8]。

纵观以往研究，对于网格加筋壳的有限元计算，若想使计算精度与试验相符，需要做到两点：a）建立精确有限元模型并使用适当的算法；b）根据壳段实测材料数据、几何缺陷修正理想模型并计算。

本文研究的内容在于获取高精度模型，梳理现有等边三角形网格加筋壳建模方法，指出不足，提出改进方法，并与标准模型进行对比，查看建模精度，最后使用实例验证。

1 等边三角形网格加筋壳建模方法

1.1 已有建模方法

等边三角形网格加筋壳自应用于新型中型运载火箭以来，如何使用有限元建模就是难点。常规有限元建模主要有两种：a）通过中间格式，如STEP、Parasolid等，将CAD三维模型导入有限元分析软件；b）基于CAD模型参数，在有限元中重构模型。

对于第1种方式，将等边三角形网格加筋壳实体模型导入后，由于斜向筋条为螺旋线实体，且与纵向实体筋条相互交叉，难以划分高质量六面体网格，而且即便划分出网格，为保证求解精度，也会造成分析模型过大。对于薄壁结构稳定性这种几何非线性、材料非线性集中的问题，大的计算规模将大幅提高计算时间，难以在短期内获取结果。因此最好的方法是使用第2种方式，即在有限元软件中重构壳模型，这样计算规模可控，同时精度也有保障，但这种方法受限于建模能力不易实施。

王博等人认为等边三角形筋条为螺旋线，在与圆柱壳和纵向筋条相交时，由于有限元软件几何建模非其擅长，容易造成交叉异常、极小边等各种几何问题，导致建模失败。为此他们提出了基于网格移动节点的建模方法[9]。这种方法模拟了实际加工过程，即板壳先铣后弯的做法：首先建立网格加筋平板模型并划分网格，然后对网格进行节点坐标变换，将节点按指定轴旋转，从而将平面网格模型更改为圆柱壁板模型。另外通过python二次开发程序，可实现全节点坐标变换的自动化，解决了网格加筋壳建模问题，见图1。

但是由于这种方法是直接操作网格节点，因此当多块壁板拼接时合并时，要求纵缝两侧的网格节点尽量对应。另外，通常贮箱由多个单壳段组成，建模还需要将多壳段网格模型合并，需要环缝两侧节点对应。在建模过程中，若出现节点不对应，或者需要调整局部网格，则必须重新操作。即便可以使用二次开发程序自动完成弯曲过程，建模全过程也比较繁琐，重复性工作多，且需要人工仔细检查接缝的网格质量，保证节点完全对应。若能在Abaqus里建立等边三角形加筋壁板几何模型，则能从根本上解决问题。为此本文提出了自创的建模方法。这种方法还能进一步二次开发，实现输入参数后自动化建模。

1.2 建模方法

贮箱等边三角形网格加筋壳示意如图2、图3所示，模型参数列于表1。由于结构为薄壁壳，在Abaqus建模中考虑建立全壳模型，由圆筒壳、纵向加筋壳和双向斜加筋壳组成。

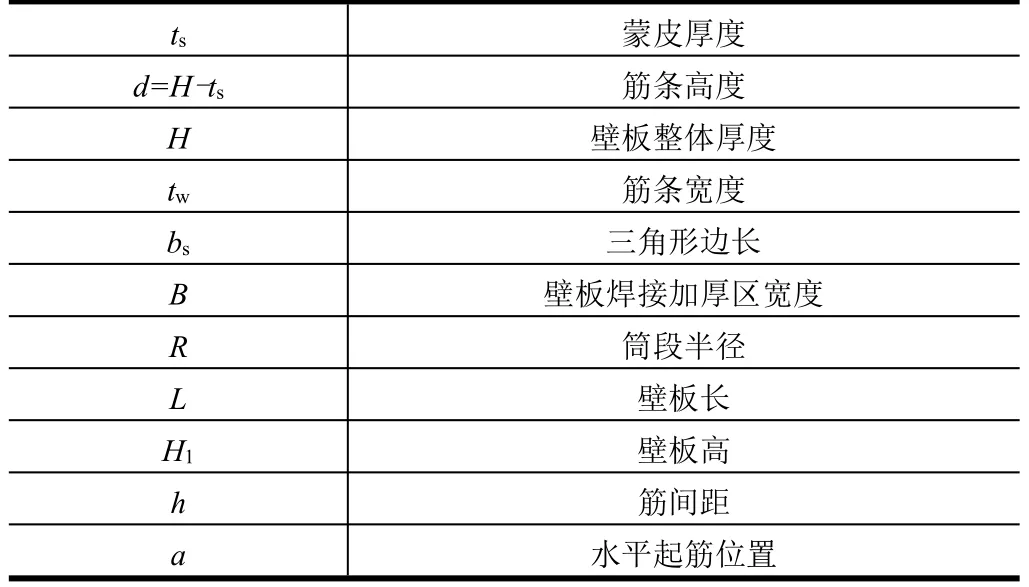
蒙皮厚度d=H-ts 筋条高度H ts壁板焊接加厚区宽度R筒段半径L壁板长H1 壁板高h筋间距a水平起筋位置壁板整体厚度tw 筋条宽度bs 三角形边长B

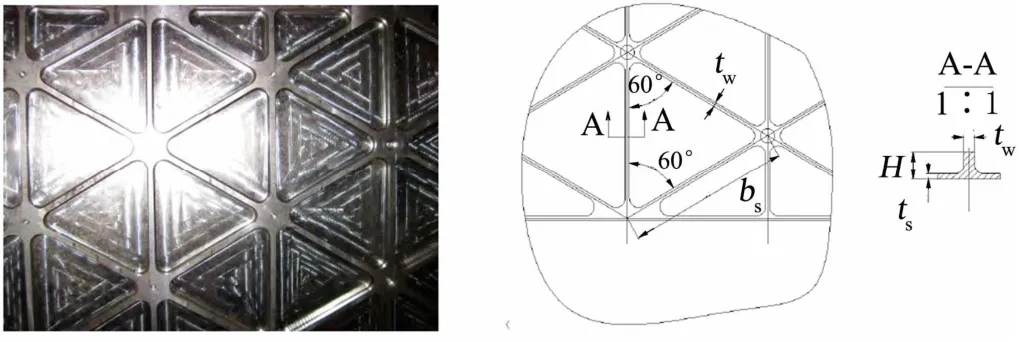
图2 等边三角形网格加筋参数示意[3]Fig.2 The Parameter of Isogrid

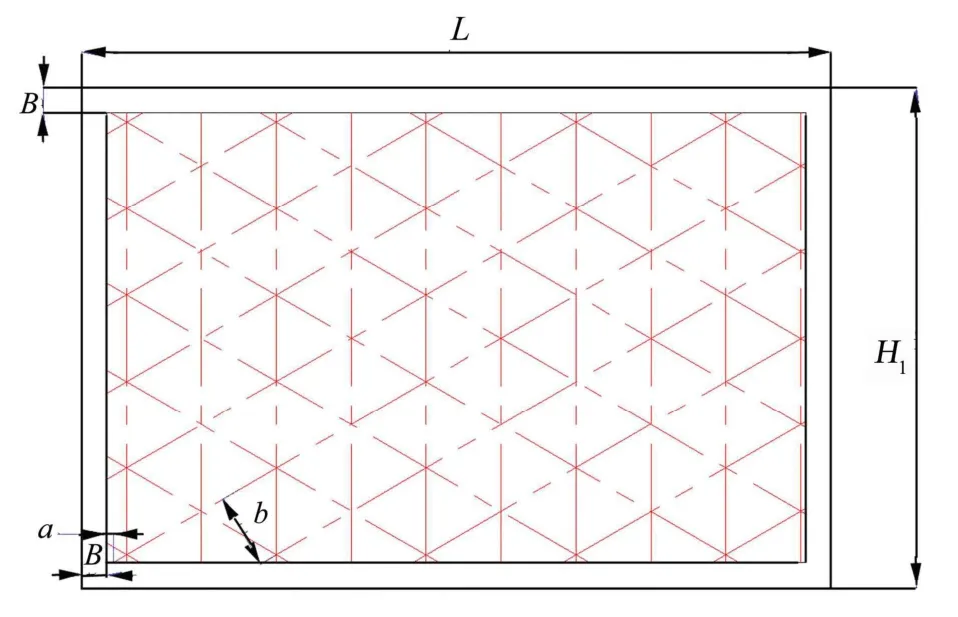
图3 贮箱等边三角形网格壁板示意Fig.3 Isogrid Shell of Tank Section

建模时需要输入螺距和阵列角。假设螺旋线角度为α，半径R，边长bs，则，螺距p为

阵列角β

以上为螺旋线通用公式。对于等边三角形网格加筋壳壁板，α=30°。由于已知螺旋角度，因此筋间距h和边长bs可以相互换算，给定一个即可。

考虑壁板加筋区域对应角度为φ，则有

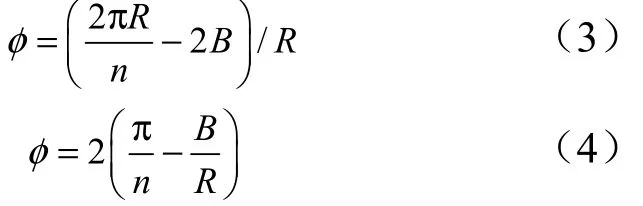
式中n为壁板个数；B为壁板焊接加厚区宽度；R为壁板筒段半径。

获得的角度为弧度制，实际建模还需要转换成角度制。从公式看，当n=1，B=0时，壁板就转化成全周期对称整体壳，相当于壳段一次加工成型，这种情况只能在很小直径壳段下实现。对于现有尺寸规模，n＞1，B≠0。除了以上参数，还需要明确起筋位置α，这样可确定加筋区域在壁板内的相对位置。

以上过程在数学上完全确定了一块贮箱壁板几何样貌，但实际上由于存在焊缝加厚区（B≠0），导致加筋范围角φ不是π的整数倍，这样造成阵列后的双向螺旋线筋条仅在部分区域与纵向筋条三面交叉于一线。因此在建立纵向筋条和圆柱面后，还需要建立多个参考面截取所需部分，才能最终获得单一壁板。

获取单一壁板后，若壁板几何完全相同，即可通过简单阵列后布尔合并得到筒段模型。若个别壁板有特殊结构，如开孔，则需要对此壁板单独处理，再和其他阵列后的常规壁板合并。

筒段建模流程如图4，按照这种思路建模并通过一定的软件技巧，可以规避文献中提到的几何建模缺陷，顺利获得高精度等边三角形网格加筋壳贮箱筒段理想模型。

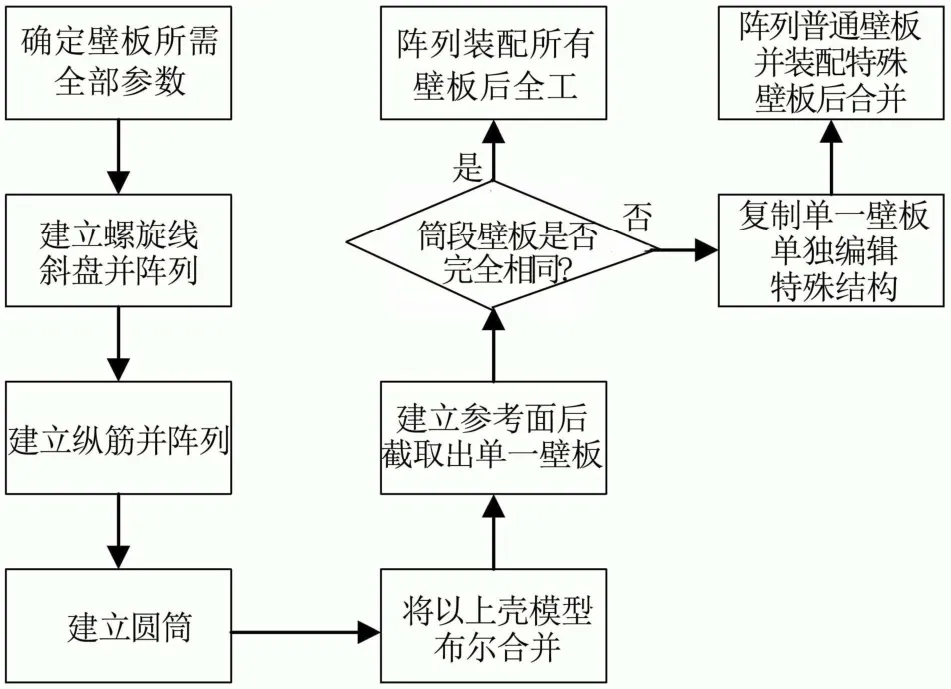
图4 等边三角形网格加筋壳建模流程Fig.4 Modeling Process of Isogrid Shell

1.3 几何精度测试

取一组测试参数建立模型。首先使用CreO建立一块等边三角形网格加筋壁板，然后使用以上方法建立模型，模型参数一致，模型如图5a，使用Abaqus建模如图5b所示。输入参数中筋间距已知，边长未知，故可使用三角形网格在纵向方向上的边长进行精度对比。

经测量，CreO模型边长和Abaqus模型边长两者相差在10-5量级，这是由于Abaqus建模精度为10-6长度单位，有截断误差，从而导致建模误差，但是两者差别仅为0.000 01%，精确度极高。

图5 网格加筋壳壁板模型Fig.5 Model of the Isogrid Tank Section

2 试验验证情况

2.1 有限元建模

在新型中型运载火箭研制过程中，需要对贮箱进行极限承载能力的试验预示。此贮箱壳段为网格加筋壳，具体试验实施方案如图6所示，工况为注水后施加轴压载荷直至破坏。

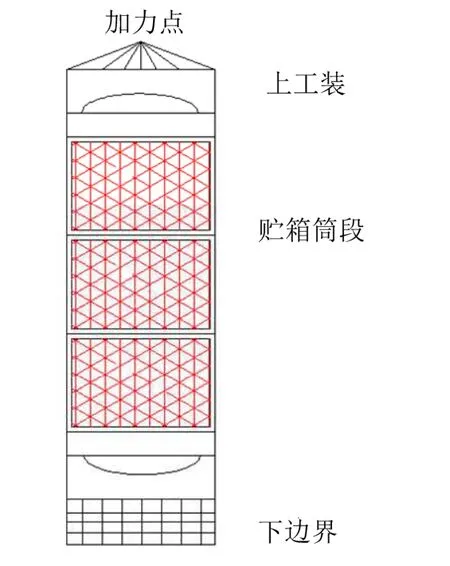
图6 试验方案示意Fig.6 Test Program

为了精确仿真，首先建立了贮箱全模型，包括前后短壳、前后箱底、叉形环、网格加筋壳筒段。筒段使用S4单元网格划分。全模型共41万单元，31万节点。

施加的载荷包括液柱压力和轴压，初步判断应在刚度较弱的第1筒段附近轴压失稳破坏。但具体破坏位置和破坏载荷需要根据计算结果提取。

建立好模型后，设置底部固支的边界条件，考虑材料非线性和几何非线性。为缩短计算时间，使用隐式方法进行计算。根据文献，若能调整好参数，隐式结果和显式结果基本相同[10]。

计算结果的位移分布如图7所示，显示在第1筒段和第2筒段之间，焊缝十字接头处附近呈失稳破坏模式。应力分布如图8所示。通过底部支反力曲线提取破坏载荷。

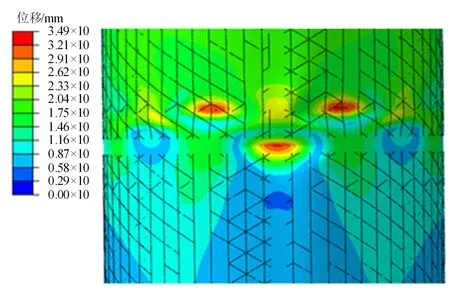
图7 筒段失效时位移分布Fig.7 Displacement Distribution of the Tank Section at Failure Moment

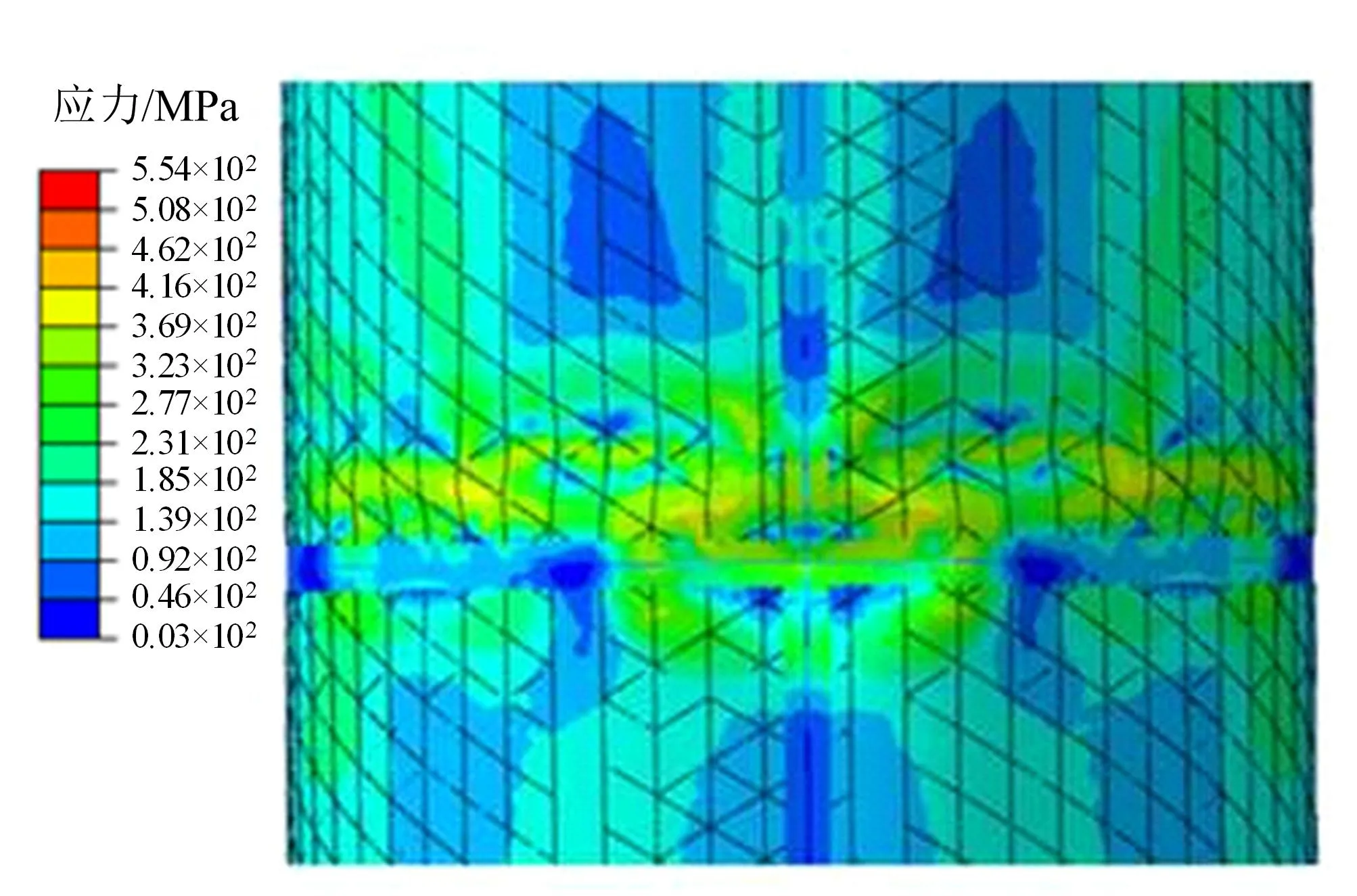
图8 筒段失效时刻应力分布Fig.8 Mises Distribution of the Tank Section at Failure Moment

2.2 计算和试验对比

a）在贮箱产品开展轴压破坏试验前，还进行了多个较大载荷的合格试验，存在由于制造、运输和试验造成的初始缺陷，因此预判最终破坏值会略低于计算值，因为计算值是在理想模型上获得的。

b）轴压破坏试验时，轴压载荷逐级加载，当达到某级载荷后继续加载时，结构突然发出较大声响，轴压载荷曲线下降，显示轴压破坏。

c）实际破坏位置位于第一筒段下部，与计算基本一致，破坏载荷两者相差1.8%，计算值略高。试验修正系数为0.98。

结果说明对于新型中型运载火箭的尺寸量级，由于加工精度较高，同时等边三角形网格加筋壳这种结构形式能够有效抵抗几何缺陷，因此使用本文方法对贮箱建模分析，可以保证试验预示的计算精度。而且相较于文献[3]，本方法的计算精度更高。

误差源可能是跟材料参数取值略保守，也可能与初始缺陷有关。如果能够对即将开展破坏试验的壳段开展光测，获得由于加工制造、运输、装配、试验等过程中可能产生的几何缺陷。那么可在理想模型基础上，按文献[9]的思路将缺陷引入，再结合加工材料实测值，即可获得贮箱基于产品状态的有限元模型，那么可进一步提高计算精度。

3 结论

a）针对某型号贮箱，使用改进的方法建立了带等边三角形网格加筋壳的贮箱模型，运用隐式算法进行分析，获得破坏形式与实际相符，破坏载荷计算值比试验值高1.8%，折减系数为0.98。充分说明了在新型中型运载火箭的尺寸量级下，等边三角形网格加筋结构能够有效抵抗几何缺陷，理想模型的计算结果与试验结果吻合度较高。但对于更大尺寸如10米量级，这一结论无法推广，还需要结合实际加工能力开展研究。

b）由于改进型方法是在Abaqus中的建模方法，可进一步使用python二次开发成基于参数化的建模程序，大幅提高建模效率。