以基本图形为支点，撬动中考压轴题

曹瑜

【摘要】复杂图形中问题的解决需要立足于对几何基本图形的熟悉，迅速识别基本图形在中考中能柳暗花明.

【关键词】基本图形;几何直观

很多中考压轴题巧妙地将多个基本图形揉合在一道题中，因多个基本图形叠加，学生不能很好地认识到图中所包含的基础图形，因而解题时一筹莫展.下面以两道中考题为例来说明.

以2016年常州卷26题为例：

（1）阅读材料：

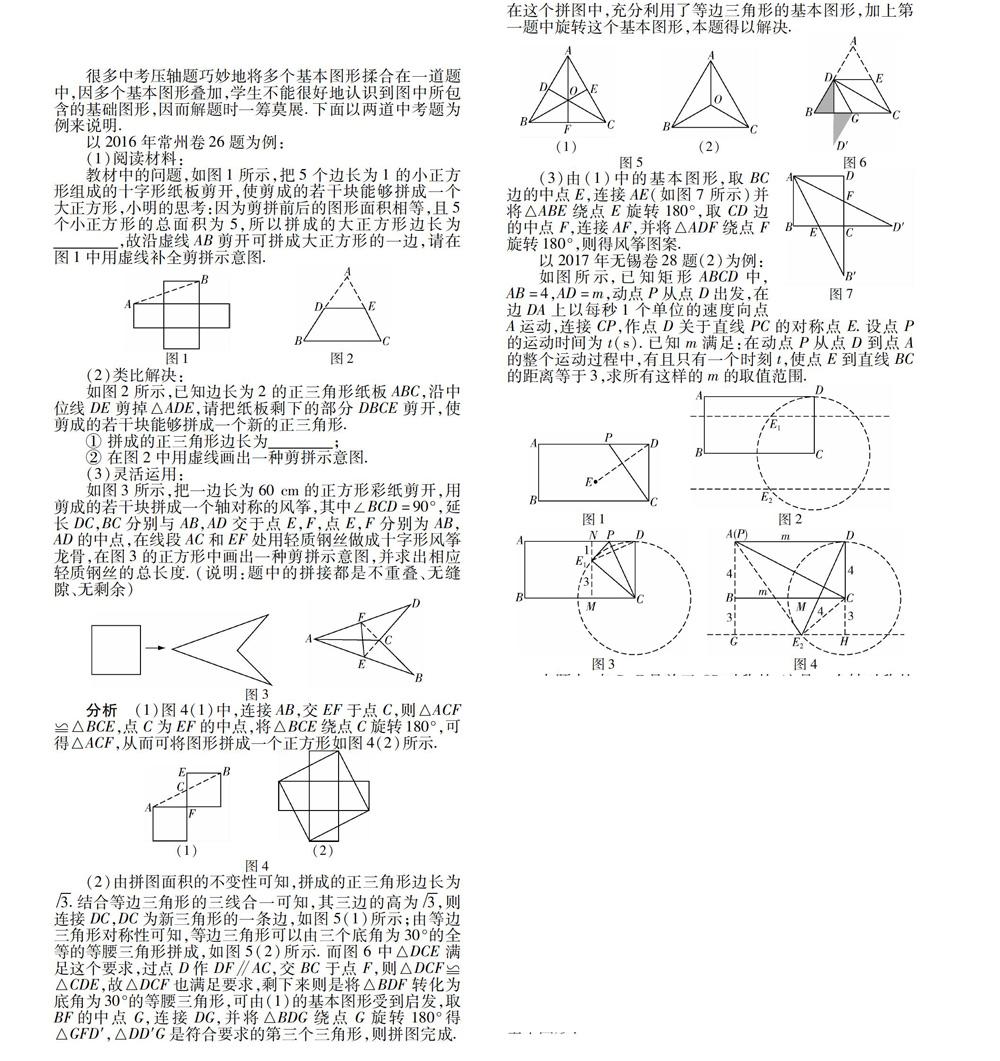
教材中的问题，如图1所示，把5个边长为1的小正方形组成的十字形纸板剪开，使剪成的若干块能够拼成一个大正方形，小明的思考：因为剪拼前后的图形面积相等，且5个小正方形的总面积为5，所以拼成的大正方形边长为，故沿虚线AB剪开可拼成大正方形的一边，请在图1中用虚线补全剪拼示意图.

本题中，点D，E是关于CP对称的，这是一个轴对称的问题.但由于点P是一个动点，所以对称轴CP是不确定的，所以无法确定点E的确切位置.由于点E是由点D对称过来的，而CD是确定的，所以点E的轨迹是可以确定的，是在以C为圆心，CD为半径的圆上.本问涉及点的轨迹的基本图形，但这个基本图形并没有给完整，只给出了定点D和运动的对称轴CP，即给出定点D和定点C，需要考生根据D，E到定点C的距离相等来把基本图形补充完整.由于P在AD上运动，所以点E在直线CD左侧的半圆上运动.由点E到直线BC的距离等于3，可以确定满足条件的E1，E2两个点，从而确定点P是在DE的垂直平分线与AD的交点处.

确定好点E的位置，可以来求相应的DP长.先看E1的情况.由于CP是对称轴，所以△CDP与△CEP关于CP对称，由轴对称的性质可知，∠PE1C=∠PDC=90°，由斜90°构造K形相似，从而过E1作E1N⊥AD，交BC于点M，构造K形相似即可求出DP.同理，求出E2的情况.

图形的直观是几何的特点，我們要充分利用这一点，要能识别出题中所给的基本图形，对只给出部分基本图形的，则要能补全基本图形，再利用基本图形顺利解决问题！因此，在平时的教学中，教师要从各个角度让学生充分认识基本图形，从而才能让学生在复杂图形中游刃有余地分离出基本图形！