基于四方向全变分的快速图像解模糊方法

林 凡，陈颖频，2，陈育群，喻 飞

(1.闽南师范大学物理与信息工程学院，福建漳州 363000；2.电子科技大学信息与通信工程学院，四川成都 610054)

由于成像系统、环境条件、记录设备、人为因素等方面的影响，数字图像往往会出现一定程度的降质现象，如图像模糊、图像噪声、部分图像信息丢失等。合理地利用降质图像及某些先验信息，设计图像优化模型并提出高效的求解算法，恢复和重建出清晰的图像，对后期的图像处理和机器视觉的研究有着重要的意义。

基于正则化的图像复原模型是行之有效的方法，1992年Rudin、Osher和Fatemi开创性地提出全变分(Total Variation，TV)正则化方法，该方法也被称为ROF模型[1]，它能较好地保持图像边缘特征，在图像去噪领域引起了广泛的关注。全变分模型分为各向异性全变分(Anisotropic Total Variation，ATV)模型和各向同性全变分(Isotropic Total Variation，ITV)模型[2]。在一阶TV模型中，图像是分片光滑的，在保持图像边缘方面具有明显的优势，但容易产生“阶梯效应”。同时，由于全变分泛函的不可微性，使得求解较为困难。此后，基于TV模型，一些延伸模型及其算法相继被提出[3-7]，被广泛地应用到图像去噪[8]、图像重建[9]和图像解模糊[10]等方面，很多图像解模糊方法通常也能起到抑制噪声的作用。例如，总广义全变分(Total Generalized Variation，TGV)模型[11]、分数阶全变分(Fractional order TV，FTV)模型[12]、非局部全变分(Nonlocal Total Variation，NLTV)模型[13]等。2011年，Sakurai等人提出四方向全变分(Four directional Total Variation，4-TV)模型[14]，将传统变分方法中仅考虑垂直和水平方向梯度信息扩展到四个方向上，以期改善去噪性能，但他们没有给出完整的数学证明。Wu等人将四方向全变分正则项进一步推广为四方向分数阶全变分稀疏正则项[15]。

为求解全变分模型，Chambolle提出了一种基于梯度的全局收敛一阶对偶算法[7]，Beck和Teboulle将投影梯度法(Gradient Projection，GP)应用到TV模型的约束性去噪问题中[16]。然而，值得指出的是，GP算法的效率取决于更新率。当更新率过大时，梯度投影法不收敛；当更新率过小时，运算效率较低。

针对以上问题，本文在图像解模糊和去噪过程中，将挖掘图像梯度的邻域结构相似性，对四方向全变分(Quaternion Total Variation，QTV)模型进行改进和完善，使用交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)进行求解。同时，在假设图像满足周期边界条件的前提下，引入快速傅立叶变换(Fast Fourier Transform，FFT)，将时域图像差分操作变换到频域中实现，有效避免大型矩阵相乘运算，从而降低计算时间，并提高计算准确度。

1 图像解模糊模型

1.1 传统的全变分模型

在图像解模糊中，考虑如下图像降质模型：

G=H*F+N.

(1)

其中，G∈N×N表示观测到的含噪声的模糊图像；F∈N×N表示由模型恢复出的图像；H∈N×N表示模糊核函数，符号*表示卷积算子。N∈N×N表示方差为σ2的加性高斯噪声。全变分正则化ROF模型表示为：

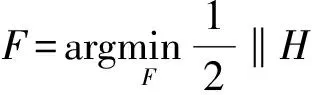
(2)

ATV模型中，R(F)定义如下：

RATV(F)=‖Kh*F‖1+‖Kv*F‖1.

(3)

ITV模型中，R(F)定义如下[2]：

(4)

其中，Kh=[-1,1],Kv=[-1,1]T分别表示横向和纵向差分卷积算子；‖·‖1表示欧式L1范数；‖·‖2表示欧式L2范数。

1.2 四方向全变分模型

从式(3)(4)可以看出，传统的全变分模型仅考虑横向和纵向这两方向的梯度信息。一个像素点被噪声污染的概率远远高于周围四个点同时都被噪声污染的概率，为了获得更好的图像重构效果，四方向全变分模型考虑更充分的邻域梯度信息，将对角线方向(45°方向和135°方向)的图像梯度作为正则约束条件[14,17]，从而提高图像复原的质量。图1为两方向全变分和四方向全变分梯度信息选取示意图[3]。

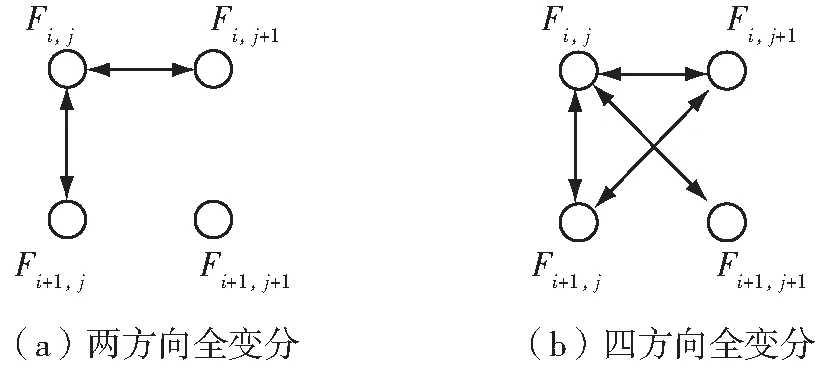
图1 四方向全变分正则项示意图

四方向全变分模型正则项定义为：

RQTV(F)=‖Kh*F‖1+‖Kv*F‖1+‖K45°*F‖1+‖K135°*F‖1.

(5)

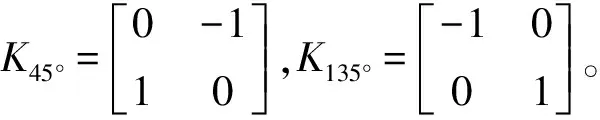
为了方便讨论，这里令K1=Kh，K2=Kv，K3=K45°，K4=K135°，四方向全变分正则化解模糊去噪模型简化为：

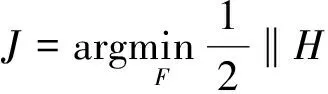
(6)

2 求解方法

令Xi=Ki*F(i=1,2,3,4)，利用增广Lagrangian方法(Augmented Lagrangian Multiplier method，ALM)解决形如式(6)的约束优化问题，将其转换成无约束问题，其目标函数可写作[18]：

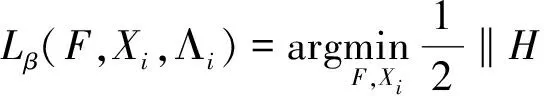
(7)

(8)

其中，变量相互独立，对于每个变量可转化为子问题进行单独求解，于是得到如下的迭代格式，k为迭代次数：

(9)

2.1 F子问题求解

对于F子问题，为了有效避免大矩阵相乘运算所带来的计算复杂性，引入快速二维傅里叶变换将时域图像差分操作变换到频域。F子问题的频域表达式为：

(10)

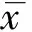
(11)

利用二维傅里叶反变换得到F子问题的最优解，整理得：

(12)

2.2 Xi(i=1,2,3,4)子问题求解

Xi(i=1,2,3,4)子问题：

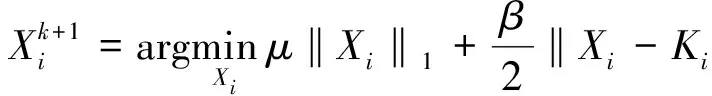
(13)

可以采用软阈值化算子(soft threshold operator)进行收缩，得到：

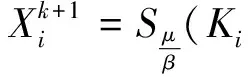
(14)

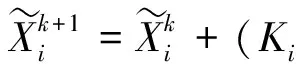
(15)

将整个算法总结于算法1，并命名为QTV-FFT。

算法1：QTV-FFT图像解模糊伪代码

输入：G

输出：F

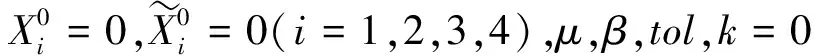
while‖Fk+1-Fk‖2/‖Fk‖2>toldo

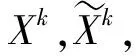
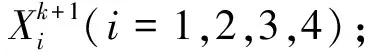
k←k+1；

end while

ReturnF

3 实验结果与分析

3.1 实验环境

选取不同风格的图像组作为实验对象，以考量本文提出的模型，测试图像如图1所示，图像大小为256×256像素。为了验证本文提出的模型的合理性和有效性，针对实验对象加入高斯模糊(Gaussian blur)或高斯随机白噪声(White Gaussian Random Noise)，进行仿真实验。硬件环境：处理器为Inter©CoreTMi7-6700CPU@3.4 GHz，内存16.0 GB。仿真平台：Matlab R2014a。对比参数主要采用图像处理领域常用的评价指标：峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)和结构相似性信息(Structural Similarity，SSIM)[20]。PSNR和SSIM的定义如下：

(16)

(17)

实验中，对比各向异性全变分ATV模型、各向同性全变分ITV模型、分数阶全变分FTV模型和本文所提频域四方向全变分QTV-FFT模型的图像恢复结果，为了保证评价的客观性和公平性，上述算法的迭代条件均当满足式(18)时迭代终止。同时，调节各种算法的正则参数，以达到各自的最佳效果，保证测试的公平性。

(18)

3.2 几种算法解模糊去噪效果的测试与比较

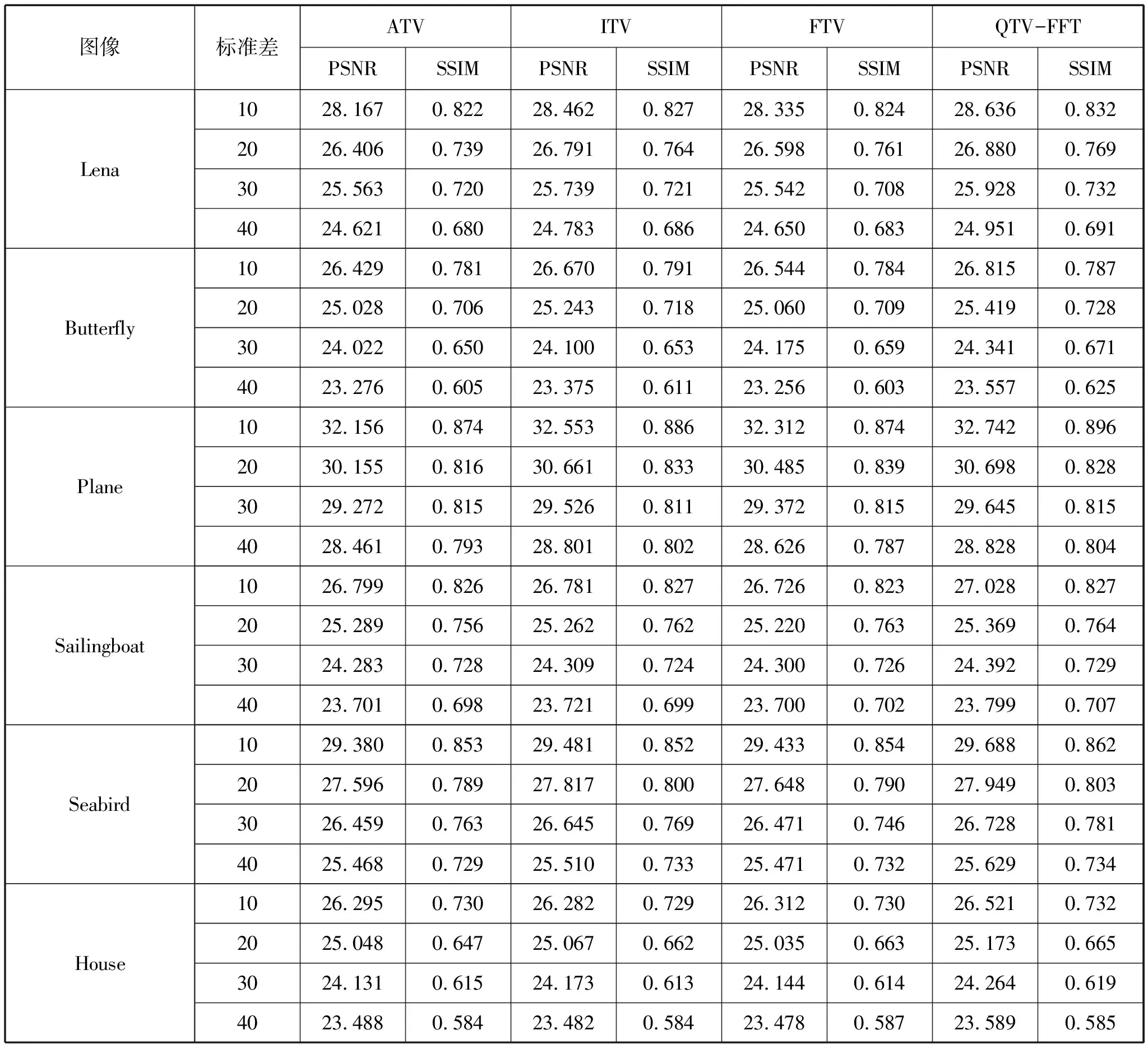
以图2图像组为测试对象，测试中使用的模糊核均由Matlab的内置函数生成，为fspecial(’gaussian’,[33],3)生成的窗口大小为3×3、标准差为3的高斯模糊核；噪声为加性高斯随机白噪声，噪声标准差σ分别为10、20、30、40。对不同图像的测试结果如表1所示，将最优指标用黑色粗体标出。

图2 测试图像组

图像标准差ATVITVFTVQTV-FFTPSNRSSIMPSNRSSIMPSNRSSIMPSNRSSIMLena1028.1670.82228.4620.82728.3350.82428.6360.8322026.4060.73926.7910.76426.5980.76126.8800.7693025.5630.72025.7390.72125.5420.70825.9280.7324024.6210.68024.7830.68624.6500.68324.9510.691Butterfly1026.4290.78126.6700.79126.5440.78426.8150.7872025.0280.70625.2430.71825.0600.70925.4190.7283024.0220.65024.1000.65324.1750.65924.3410.6714023.2760.60523.3750.61123.2560.60323.5570.625Plane1032.1560.87432.5530.88632.3120.87432.7420.8962030.1550.81630.6610.83330.4850.83930.6980.8283029.2720.81529.5260.81129.3720.81529.6450.8154028.4610.79328.8010.80228.6260.78728.8280.804Sailingboat1026.7990.82626.7810.82726.7260.82327.0280.8272025.2890.75625.2620.76225.2200.76325.3690.7643024.2830.72824.3090.72424.3000.72624.3920.7294023.7010.69823.7210.69923.7000.70223.7990.707Seabird1029.3800.85329.4810.85229.4330.85429.6880.8622027.5960.78927.8170.80027.6480.79027.9490.8033026.4590.76326.6450.76926.4710.74626.7280.7814025.4680.72925.5100.73325.4710.73225.6290.734House1026.2950.73026.2820.72926.3120.73026.5210.7322025.0480.64725.0670.66225.0350.66325.1730.6653024.1310.61524.1730.61324.1440.61424.2640.6194023.4880.58423.4820.58423.4780.58723.5890.585

从表1可以看出，在对不同图像加入不同程度的模糊和噪声后，本文提出的模型对图像重建时的PSNR值均高于其它几种方法，SSIM值也基本高于其它几种方法。这表明该模型具有较好的解模糊和去噪效果，同时恢复出的图像与原始图像更为接近。为了进一步观察测试结果，下面给出几组测试结果对比图。

图3 几种算法恢复图像对比图

图4 几种算法恢复图像细节对比图

图3是对Sailingboat图像加入窗口大小为3×3、标准差为3的高斯模糊核和σ=30的高斯噪声后几种算法恢复的图像对比图；图4是对Butterfly图像加入窗口大小为5×5、标准差为5的高斯模糊核和σ=30的高斯噪声后几种算法恢复的图像细节放大对比图。从恢复图像的视觉效果来看，本文方法在保护图像轮廓边缘的同时，较好地处理了图像平滑区域灰度值相近的像素点的重建，避免了阶梯效应，去噪整体性能良好。

以Plane图像为测试对象，测试中使用的模糊核分别为窗口大小为3×3、5×5、7×7、9×9，标准差为5的高斯模糊核，高斯噪声标准差σ=50。采用本文方法复原图像如图5所示。图6是对House、Butterfly、Lena、Seabird图像使用的模糊核窗口大小为5×5、标准差为5的高斯模糊核并加入不同标准差的高斯噪声后，分别用ATV模型和QTV-FFT模型恢复图像的对比图。从图5、图6恢复图像的视觉效果来看，本文方法在不同模糊核和不同噪声浓度的情况下复原图像均有不俗的表现。在高污染噪声的情况下，本文方法恢复的图像依然具有良好的视觉效果。

图5 不同模糊核下QTV恢复图像效果图

图6 不同噪声下ATV和QTV-FFT恢复图像对比图

3.3 几种算法图像恢复时间测试与比较

为了进一步检验所提模型的时效性，在保证测试公平性的前提下，本节对比了ATV、FTV、QTV-GP、QTV-FFT模型对图像重建时的平均耗时(Mean Time)。其中，把时域中利用投影梯度法算法(Gradient Projection，GP)求解四方向全变分的模型记为QTV-GP模型，本文提出的频域四方向全变分ADMM算法记为QTV-FFT模型。测试中，向图1测试图像组加入窗口大小为3×3、标准差为3的高斯模糊核和σ分别为10、20、30、40的高斯噪声。测试结果如表2所示。

表2 几种算法对不同图像解模糊去噪的平均耗时(s)

分析表2数据可以看出，四方向全变分模型考虑更充分的邻域梯度信息，增加了对角线方向的图像梯度作为正则约束条件，增大了计算量，因此QTV-GP模型对图像重建的耗时较长，均高于ATV和FTV模型的耗时。而本文提出的QTV-FFT模型，引入快速傅立叶变换，将时域图像差分操作变换到频域，有效避免大矩阵相乘运算，不仅降低了计算时间，还提高了计算的准确度。

4 结论

本文从四方向全变分正则项出发，结合全变分图像解模糊去噪方法，基于ADMM算法和快速傅立叶变换提出一种改进的广义全变分图像复原方法。充分挖掘了图像梯度的各方向信息，通过设定合理的阈值，有效去除图像模糊和噪声，减弱阶梯效应，较好地保留图像的边缘信息。同时将时域图像差分操作变换到频域，有效避免大矩阵相乘运算，提高算法效率。为验证算法的合理性和有效性，将提出方法与几种经典算法进行比较。测试结果表明，本文方法图像恢复效果优于其它几种算法，对图像重构整体性能良好。