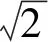粗糙球形表面的分形接触力学模型
2019-04-29原园张利华徐颖强
原园,张利华,徐颖强
(1.西安理工大学机械与精密仪器工程学院,710048,西安;2.西北工业大学机电学院,710072,西安)
接触现象广泛存在于工程领域中。掌握物体之间的接触力学性能,对研究润滑、摩擦、磨损及热传导等具体的工程实际问题具有十分重要的作用。经典接触力学中普遍认为物体的接触表面是光滑连续的,当两物体接触时,其间的实际接触面积与名义接触面积是相等的。然而,实验观测表明,物体的接触表面是由众多几何尺寸不同的微凸体构成,即接触表面是粗糙表面。由于两个物体的接触实际是两接触面上微凸体的相互作用,使得实际接触面积远远小于名义接触面积,真实接触面积承受过大的接触载荷,导致接触面的压溃、磨损,引起接触零部件的失效。因此,研究粗糙表面在接触过程中真实接触面积与接触载荷的关系,对提高接触零部件的承载能力和使用寿命具有十分重要的理论指导作用。
目前,粗糙表面接触问题的研究对象以平面接触为主,研究方法主要从实验测试[1-2]和理论研究两方面进行。实验测试可以直观地得到粗糙表面接触过程中的各项力学性能规律,验证接触零部件是否满足设计要求,但实验测试结果对仪器的测量精度和实验环境较为敏感,测量结果只在一定范围(材料属性、表面形貌、载荷历程等)内有效,不具有普遍性。理论研究所建立的力学模型和计算方法具有一定的普遍适用性,因此得到长足发展。在理论研究中,粗糙表面接触力学模型主要分为统计学模型、分形模型、多尺度模型[3-4]、确定性模型[5]及有限元模型[6],这些模型各具优势。多尺度、确定性和有限元模型考虑到微凸体相互叠加的因素,更准确地反映了粗糙表面的真实面貌。统计学模型和分形模型将微凸体简化为半球体,获得了粗糙表面接触过程中真实接触面积和接触载荷的关系。由于这两种模型求解简便,易于扩展到不同的工程领域,应用较为广泛。
Greenwood和Williamson于1966年首次建立了粗糙表面接触的统计学模型,即GW模型[7]。在该模型中,所有微凸体的曲率半径被认为是相同的,其高度服从高斯分布,并且引入塑性指数作为评判微凸体发生弹性或塑性变形的依据,进而推导出粗糙表面真实接触面积和接触载荷的关系。随后,GW模型被不断扩展来满足不同的工况要求,例如材料的弹塑性变形[8]、材料的黏弹性变形[9]、弹塑性变形的卸载[10]、微凸体的相互作用[11]等,这些研究成果使得GW模型日趋完善。Mandelbrot于1982年观测到物体表面形貌轮廓呈现出连续、不可微和自相似的特征,满足分形的几何特性[12]。随后,Majumdar等采用Weierstrass-Mandelbrot函数模拟出二维粗糙表面轮廓[13],Majumdar和Bhushan根据二维分形表面轮廓的特征,认为微凸体的分布形式服从海洋岛屿的分布规律,建立了二维粗糙表面接触力学模型,即MB模型,获得了真实接触面积与接触载荷的解析表达式[14]。由于MB模型易于直接得到真实接触面积与接触载荷的解析解,很快被应用到工程中的众多具体问题,例如:三维粗糙表面接触[15]、焊接材料界面的接触率[16]、接触面的黏着磨损[17]、结合部的法向刚度[18]等。然而,在MB模型中,粗糙表面的微凸体在接触过程中首先发生完全塑性变形,随着接触下压量的增大,微凸体的变形逐渐转变为弹性,该现象与经典的赫兹接触模型矛盾。对此,Morag等修正了分形模型中单个微凸体的弹塑性接触模型,使微凸体的变形过程与赫兹接触模型保持一致[19]。Yuan等人修正了传统的MB模型[20]。在修正模型中,微凸体的变形过程符合赫兹接触理论,微凸体在接触过程中承担的接触面积和接触载荷与其曲率半径成正比。该模型也被应用到三维接触[21]、线接触[22]及接触卸载[23]等具体问题。
基于上述研究成果,根据分形理论,本文建立了球形分形粗糙表面的接触力学模型。球形分形粗糙表面是一个曲面,将粗糙表面的接触区域分成N份,每份接触区域都可以等效成一个平面接触问题。推导每份接触区域上各个频率指数的微凸体的截断面积密度分布函数,获得真实接触面积与总接触载荷的解析表达式,即可得到接触半宽上的接触压力分布规律。本文可为机械工程领域的点接触问题的理论研究、零部件设计提供一定的理论依据。
1 球形分形粗糙表面的表征
在球坐标系(r,φ,φ)中,各向同性的球形分形粗糙表面的方程[24]为
W(r,φ,φ)=r+r(G/r)D-2(lnγ/MS)1/2·
(1)
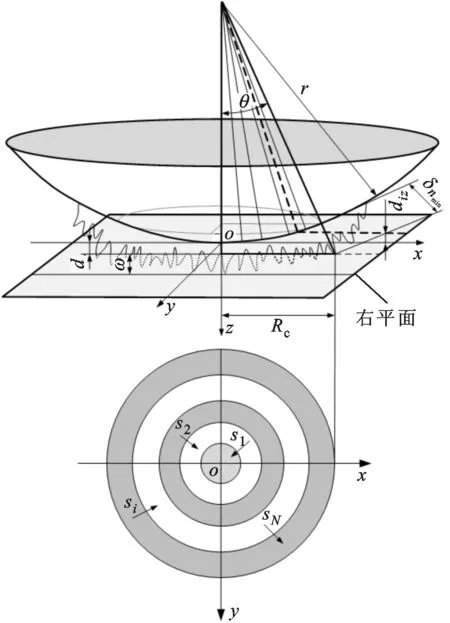
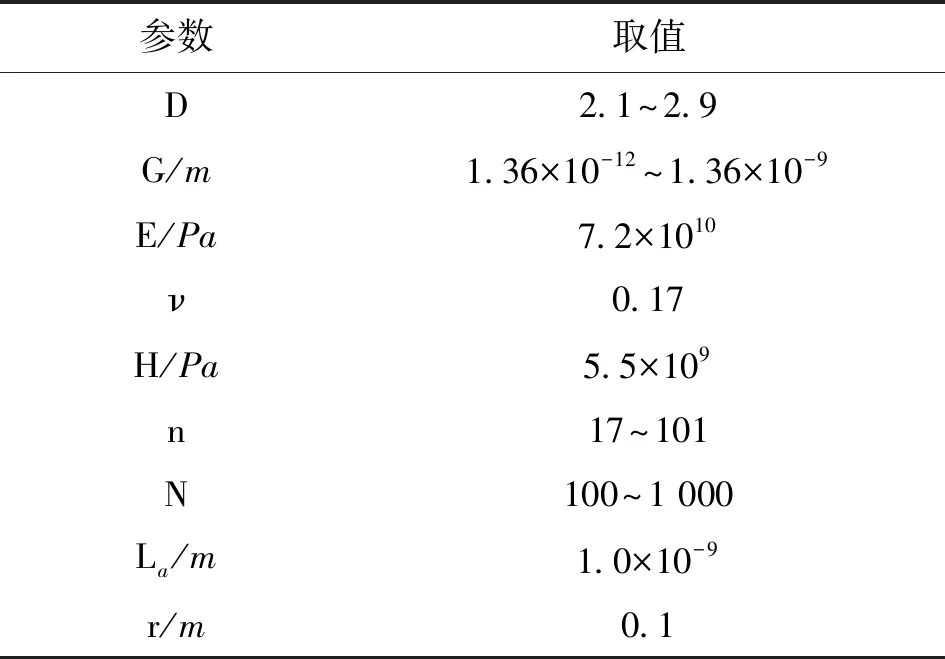
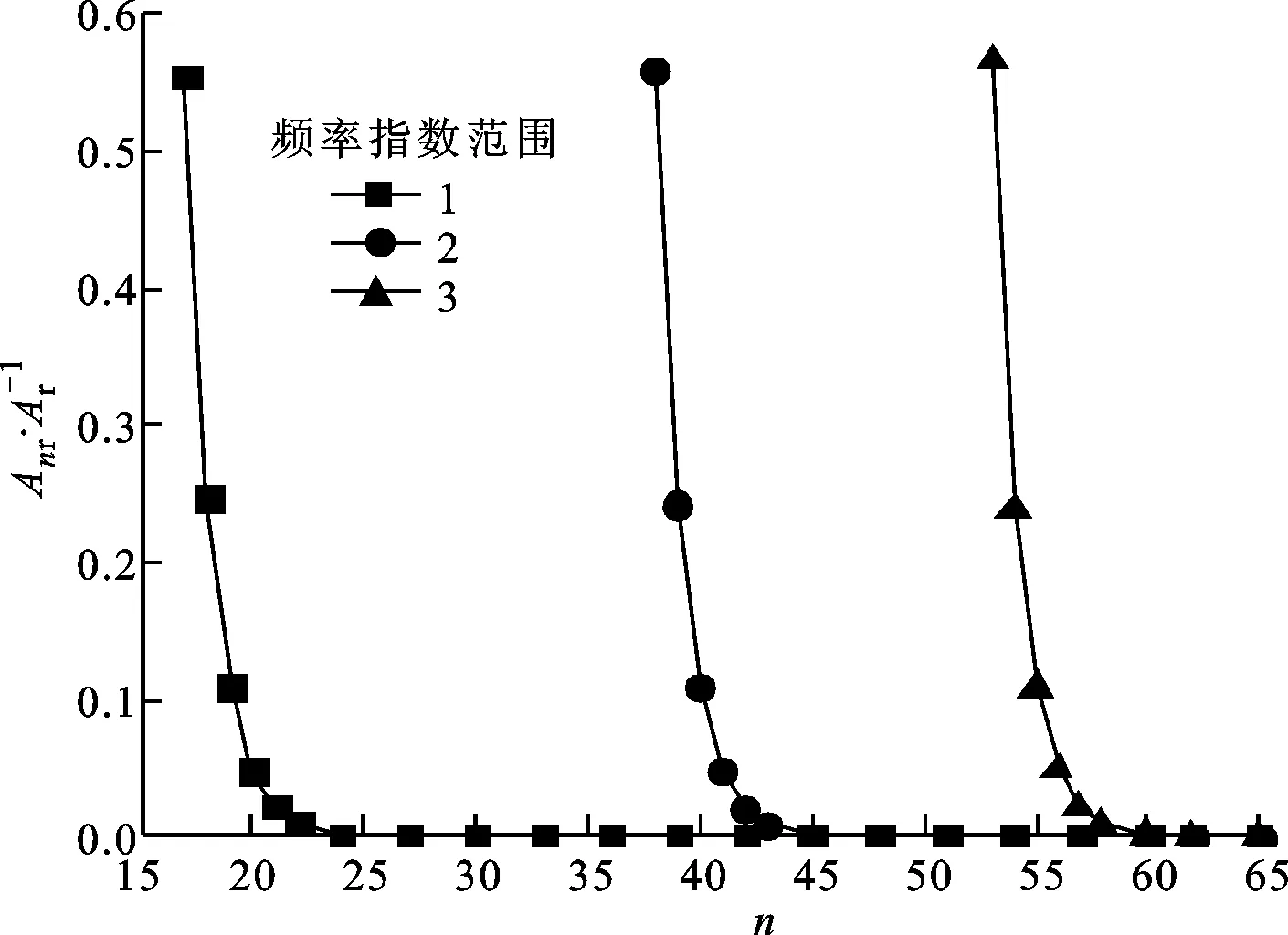
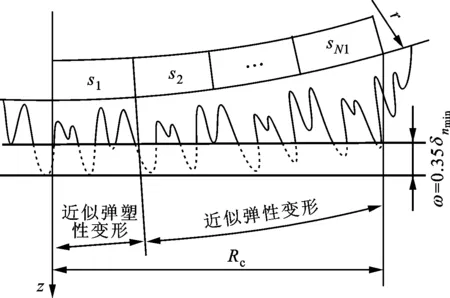
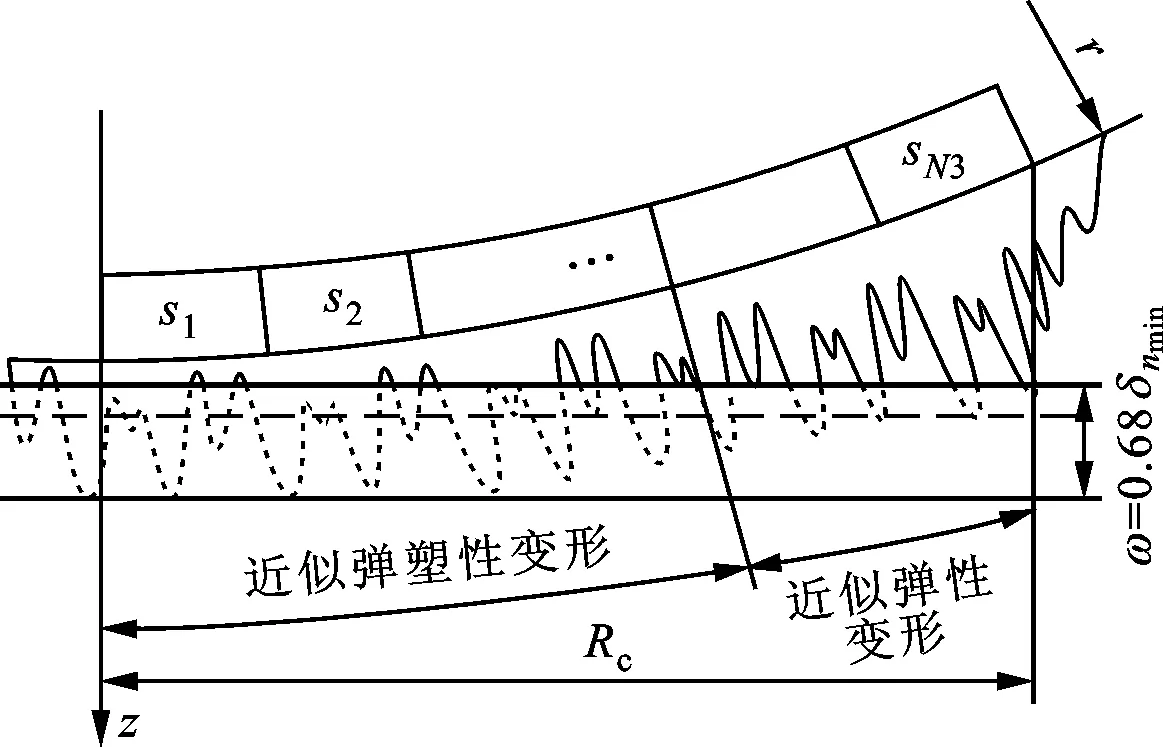
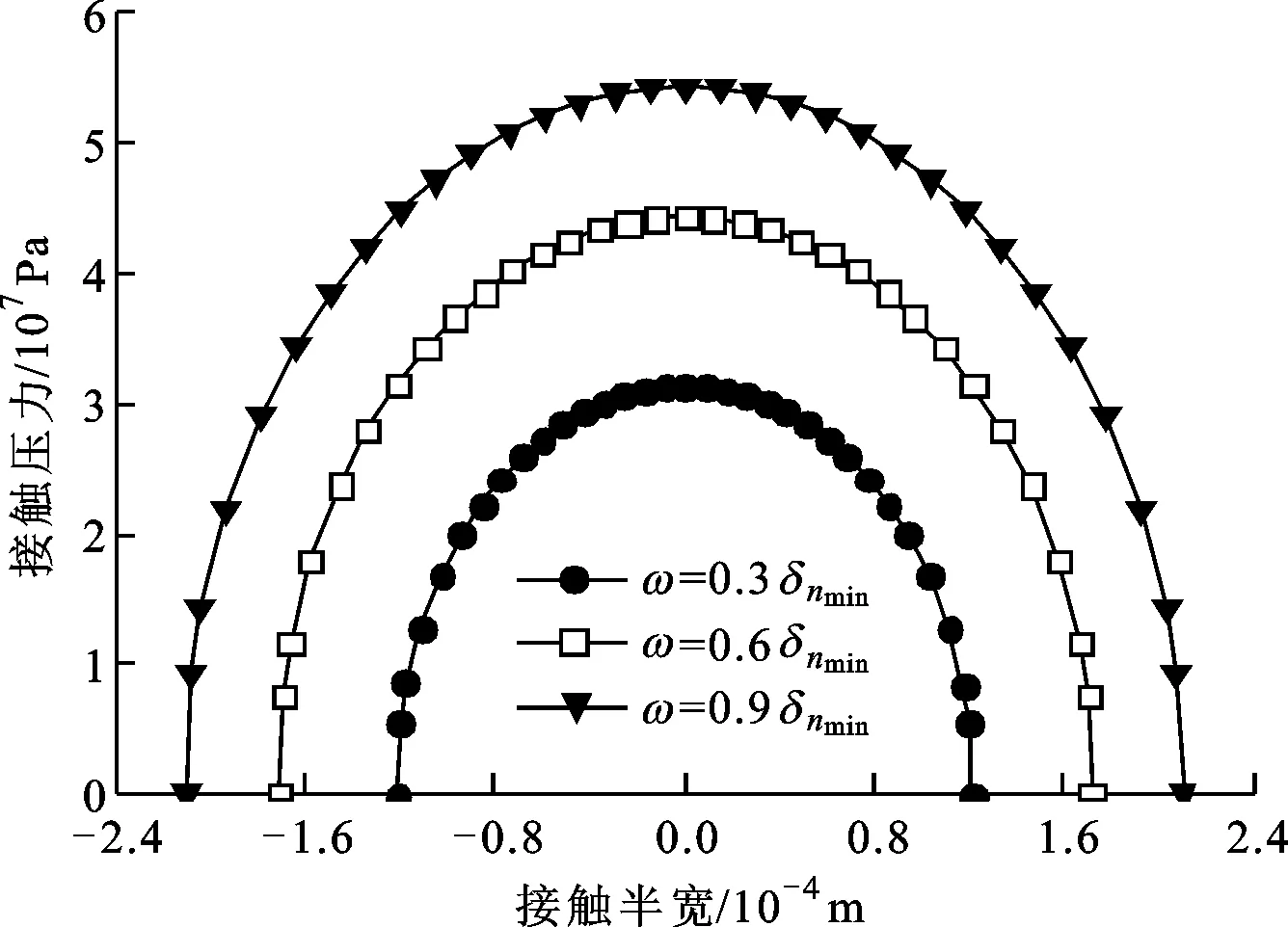
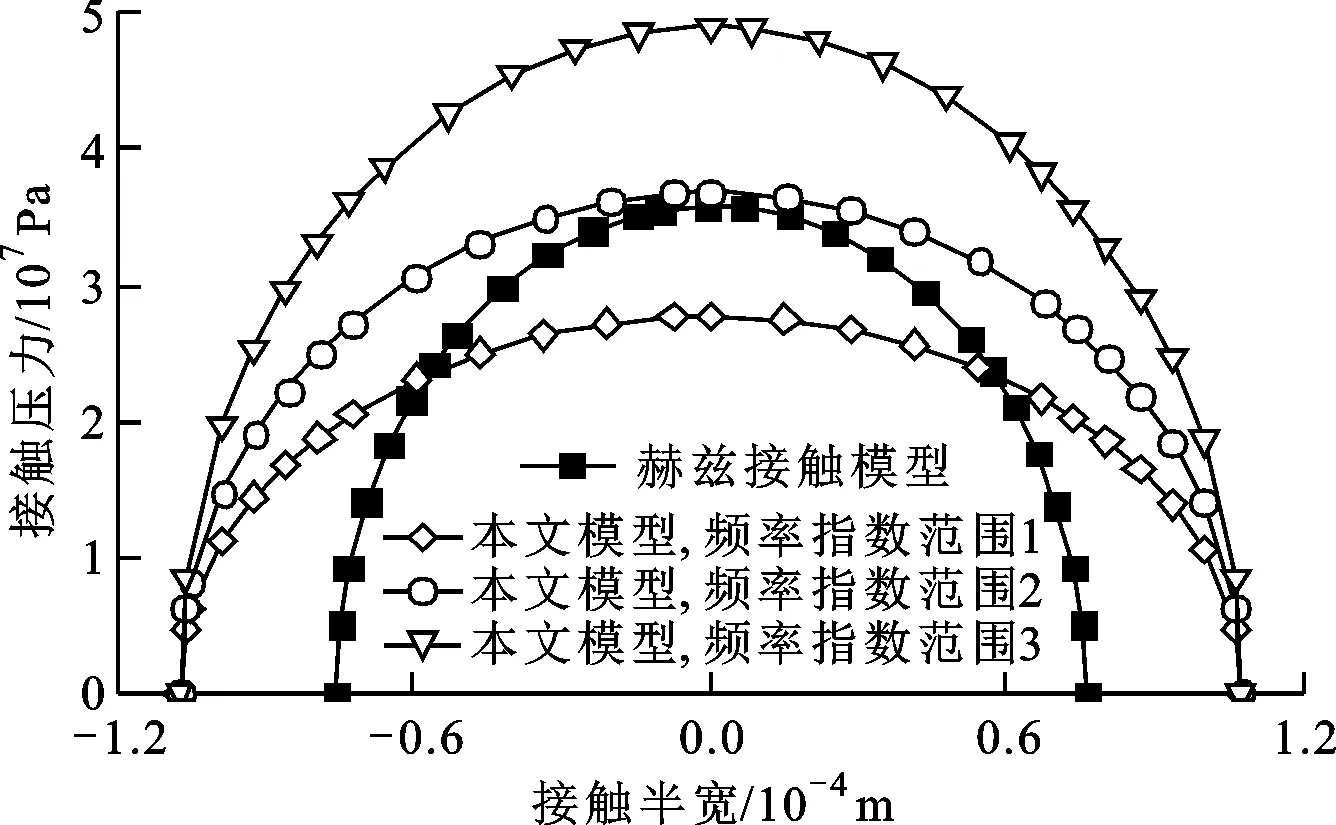
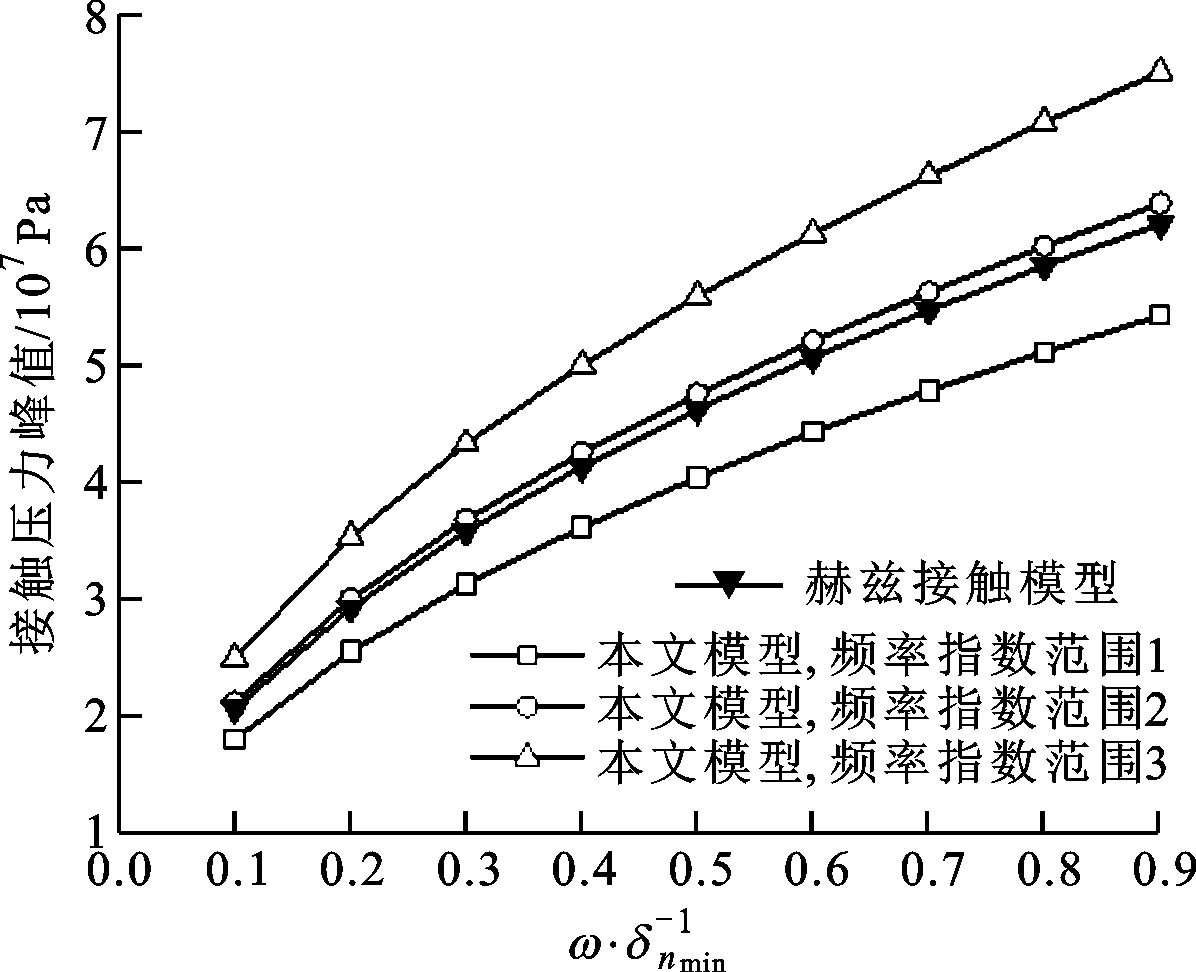
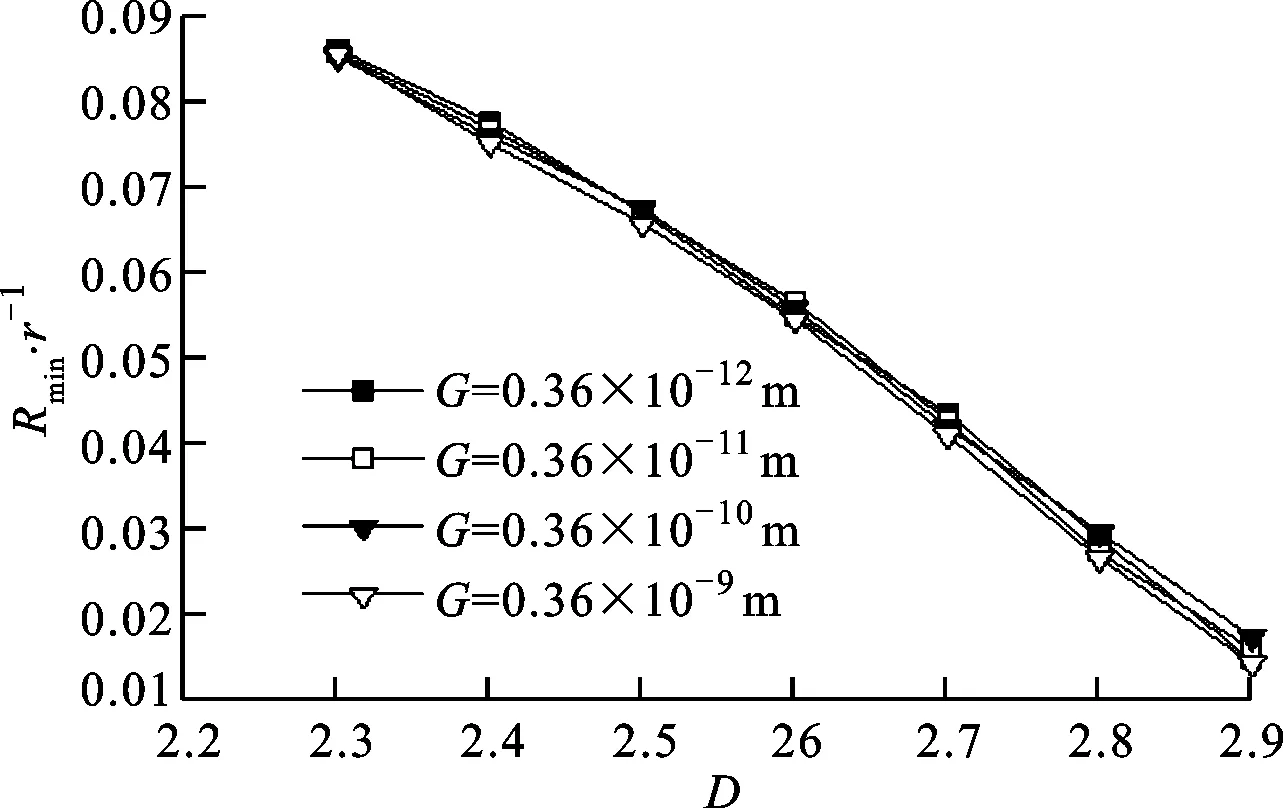
式中:W(r,φ,φ)表示粗糙表面上任意一点到圆心的距离,r为球形分形粗糙表面的基圆半径,φ为从z轴正方向看r在xoy平面上的投影与x轴正方向的夹角,φ为r与z轴正方向的夹角;ψm,s,n为随机相位,m和s分别为φ方向和φ方向上重叠隆起部的数量,M和S分别为其最大值,n为微凸体的频率指数;γ为随机轮廓的空间频率,通常情况下取γ=1.5;D为分形维数,对于三维表面轮廓,D的取值范围为2 nm,su=r[sin(φα)sin(φ)cos(φ-φα)+ cos(φα)cos(φ)] (2) 式中:φα=πs/S;φα=2πm/M。 若不考虑微凸体之间的相互重叠,则粗糙球形表面上对应φ方向与φ方向上的重叠隆起部的个数为1。令M=S=1,得到φα=π,φα=2π,带入式(2)可得nm,su=rcosφ。基于上述简化过程,式(1)可变换为 W(r,φ,φ)=r+r(G/r)D-2(lnγ)1/2· (3) 式中:ψnψ1,1,n;粗糙球形表面上微凸体频率指数范围从nmin变化到nmax,二者之间的关系为nmax=nmin+int[log(L/La)/logγ],int[]表示取括号内的值的整数部分,L为粗糙表面的取样长度,对于粗糙球形表面,L=r[24],La为截止长度。采用式(3)生成D=2.3、G=2×10-5m时的粗糙球形表面,并在直角坐标系xyz下进行表示,结果如图1所示。 图1 三维粗糙球形表面轮廓 粗糙表面上的微凸体的力学性能直接影响粗糙表面的力学性能,因此必须先确定单个微凸体在接触过程中接触载荷和接触面积的关系。假设粗糙球形表面上的微凸体之间不发生相互作用,微凸体的几何外形为半球形。在第i份接触区域中(接触区域的划分在第3节中详细描述),根据式(3),直角坐标下频率指数为n的微凸体未变形前的轮廓方程为 (4) 式中:Zi,n表示单个微凸体轮廓曲线上任意一点的高度;ψi,n为(0,2π)范围内随机相位。 图2表示了该微凸体与一刚性平面接触的情况,虚线部分为微凸体的原始轮廓,实线部分为微凸体的变形轮廓。 图2 单个微凸体接触模型 图2中:li,n为微凸体的基底长度,与取样长度L的关系为li,n=L/γn[24];ωi,n为刚性平面的下压量;δi,n为微凸体的高度,表达式为 δi,n=GD-2(lnγ)1/2(L/γn)3-D (5) Ri,n为对应的顶端曲率半径,表达式为 (6) (7) (8) 当n (9) (10) (11) 从式(10)(11)可以看出,ai,nec≤ai,nep≤ai,nepc,ai,nepc为临界弹塑性接触面积,ai,nepc=153.6ai,nec。当n (12) (13) (14) 一个粗糙球形表面与一个粗糙平面接触可以转化为一个粗糙球形表面与一个刚性平面接触,接触过程中基圆不发生变形,如图3所示。 图3 粗糙球形表面与刚性平面接触示意图 图3中:d为刚性平面与基圆底部之间的距离;ω为刚性平面的下压量;δnmin表示频率指数为nmin的微凸体高度,δnmin与d之间的关系为ω+d=δnmin。粗糙球形表面与刚性平面之间的接触区域是一个半径为Rc的圆。在接触区域与非接触区域的边界上,假设刚性平面刚好与频率指数为nmin的一个微凸体顶端相切,则Rc可表示为 (15) 与接触半宽Rc对应的圆心角为θ。若将圆心角θ平均分成N份,则接触区域也被分为N份。s1表示接触区域的第一份,s2表示接触区域的第二份,si表示接触区域的第i份,其中接触区域的第一份为圆形,其余各份为环形。至此,粗糙球形表面接触问题转化成N个平面接触问题。当刚性平面的下压量为ω时,每份对应的下压量也不同,第i份的下压量可表示为 ωi=δnmin-(δnmin-ω+diz)/cosθi (16) (17) 其中i∈[1,N] 整个接触区域包含频率指数从nmin到nmax的微凸体,将整个接触区域分成N份,每一小份接触区域中同样包含频率指数从nmin到nmax的微凸体。若用a′表示微凸体的接触截断面积,则整个接触区域上微凸体截断面积密度分布函数n′(a′)的表达式[15]为 (18) (19) (20) 式中ξi(N)为第i份的微凸体截断面积密度分布函数修正系数,与第1份的修正系数ξ1(N)的关系为 ξi(N)=Δi(N)ξ1(N) (21) 其中Δi(N)=si(N)/s1(N)=2i-1,s1(N)表示第一份接触区域的名义面积,si(N)表示第i份接触区域的名义面积。 (22) (23) (24) (25) 为简化计算,令Λi,min=Λi,min+1=…=Λi,max-1=Λi,max=Λi,根据文献[20],可得 (26) (27) 球形分形粗糙表面与刚性平面接触时,整个接触区域上的所有微凸体可能发生弹性变形、弹塑性变形或完全塑性变形。整个接触区域的真实接触面积Ar可以表示为 Ar=Are+Arep+Arp (28) 式中Are、Arep和Arp分别是由弹性变形、弹塑性变形和完全塑性变形引起的真实接触面积,分别表示为 (29) (30) (31) 与真实接触面积对应的总接触载荷可表示为 Fr=Fre+Frep+Frp (32) 式中Fre、Frep和Frp分别是由弹性变形、弹塑性变形和完全塑性变形引起的总接触载荷,这三个部分可以表示为 (33) (34) (35) 第i份接触区域上的接触压力pi为 pi=Fi,r/Ai,r, 1≤i≤N (36) 式中Ai,r和Fi,r分别是第i份接触区域上的真实接触面积和总接触载荷,可以表示为 (37) (38) 根据推导出的解析结果,研究粗糙球形表面接触过程中真实接触面积和总接触载荷之间的关系。粗糙球形表面的各项计算参数[15]如表1所示。 表1 计算参数 接触区域被分成N份,每份都包含不同频率指数的微凸体,分别独立给出每个频率指数微凸体的最大截断面积会导致结果数据冗余且无规律可循。为了使计算结果符合实际情况,规定在第i份接触区域内,各个频率指数的微凸体中具有最大截断面积的微凸体,其接触下压量与自身高度的比值都相同。根据表1的数据,可以得到微凸体的临界弹性频率指数nec=33,临界弹塑性频率指数nepc=46。 (a)ω=0.5δnmin (b)ω=0.4δnmin和ω=0.8δnmin图4 不同频率指数范围微凸体产生的真实接触面积与总真实接触面积的比值变化 图5表示当微凸体频率指数范围为17~65、ω=0.95δnmin时,粗糙球形表面接触过程中总真实接触面积Ar与总接触载荷Fr的关系,可以看出:粗糙球形表面在整个接触过程中近似表现为弹性性质,总接触载荷与真实接触面积的3/2次方成正比,即Fr~Ar3/2。这是因为临界弹性频率指数nec=33,所以频率指数处于17~33的微凸体只能发生弹性变形。又由于在分形粗糙表面接触过程中,前6个频率指数的微凸体对整个接触过程起主导作用,即使频率指数处于34~65的微凸体发生弹塑性或完全塑性变形,其比例在总接触载荷和总真实接触面积中小于0.01。 图5 真实接触面积与总接触载荷的关系 图6与图7表示微凸体频率指数范围为38~86时,粗糙球形表面接触过程中的变形状况。频率指数处于38~46的微凸体在接触过程中可以发生弹性变形和弹塑性变形,频率指数处于47~86的微凸体可以发生弹性变形、弹塑性变形及完全塑性变形。 图6 真实接触面积与总接触载荷的关系 图7为接触区域的变形状况。图7a是当ω=0.35δnmin时的接触区域变形情况,可以看出:接触区域被分成N1份(N1=100);第1份接触区域发生弹塑性变形,其余各份接触区域都呈现近似弹性变形。因为弹塑性变形与总变形的比值十分小,此时接触变形状态仍呈现为弹性性质。图7b和图7c分别是当ω=0.52δnmin和ω=0.68δnmin时的接触区域变形情况,可以看出:随着接触下压量的增加(接触区域增大,接触区域所分的份数也逐渐增加,以确保不同下压量下第i份接触区域的面积近似保持一致),弹塑性变形区域逐渐增大,弹塑性变形占总变形的比例也逐渐增大。当这个比例大于60%时,粗糙球形表面逐渐显现弹塑性变形性质。 (a)ω=0.35δnmin (b)ω=0.52δnmin (c)ω=0.68δnmin图7 接触区域的变形状况 图8 真实接触面积与总接触载荷的关系 图9表示接触区域上接触压力的分布规律。图9a表示当微凸体频率指数范围为17~65时的情况,可以分析得出:粗糙球形表面的接触半宽与接触压力成正比;粗糙球形表面在接触过程中呈现弹性性质,压力分布曲线近似抛物线,与赫兹接触模型的压力分布较为相似。图9b表示当微凸体频率指数范围为38~86时的情况,可以分析得出:当ω=0.3δnmin时,粗糙球形表面呈现弹性变形性质,接触压力分布近似为抛物线;当ω=0.6δnmin和ω=0.9δnmin时,粗糙球形表面呈现弹塑性变形性质,接触压力分布曲线的顶端变得较为平缓。图9c表示当微凸体频率指数范围为53~101时的情况,可以分析得出:当ω=0.3δnmin时,粗糙球形表面呈现弹塑性变形性质,接触压力分布曲线的顶端较为平缓;当ω=0.6δnmin和ω=0.9δnmin时,粗糙球形表面呈现弯曲塑性变形性质,接触压力分布曲线的顶端趋于直线,其轮廓近似为一个矩形,这表明接触压力在接触半宽上近似均匀分布。 (a)频率指数范围为17~65 (b)频率指数范围为38~86 (c)频率指数范围为53~101图9 接触区域上接触压力的分布规律 (a)接触半宽上压力分布的对比 (b)接触压力峰值的对比图10 本文模型与赫兹接触模型的接触压力对比 图11 本文模型与赫兹接触模型的压力峰值相等时各分形参数之间的关系 为了获得粗糙球形表面接触模型与赫兹接触模型之间的内在联系,只考虑粗糙球形表面接触的弹性变形阶段。为寻求本文模型与赫兹接触模型在接触下压量相等时,接触压力峰值也同样相等的存在条件,构建两模型中各分形参数的关系,如图11所示,图中Rmin表示最小频率指数的微凸体顶端曲率半径,可以看出,G在1.36×10-9~1.36×10-12m之间变化,对D与Rmin/r的关系影响很小。忽略G的影响,对图11中的曲线进行拟合可得 Rmin/r=f(D)=-0.063 9D2+0.197D-0.028 7 (39) 对于给定的分形维数D,最小频率指数的微凸体顶端曲率半径与基圆半径比值Rmin/r满足式(39)。对于相同的接触下压量,粗糙球形表面接触模型的接触压力峰值始终等于赫兹接触模型的接触压力峰值。如果Rmin/r>f(D),则粗糙球形表面接触模型的压力峰值小于赫兹接触模型的压力峰值;否则,粗糙球形表面接触模型的压力峰值大于赫兹接触模型的压力峰值。从工程应用考虑,为了确保接触零件的安全使用,在额定下压量的情况下,应尽量增大表面微凸体顶端曲率半径,降低表面粗糙度。 (1)微凸体的频率指数范围直接影响粗糙球形表面的接触力学性质,前6个频率指数的微凸体在整个接触过程中起主导作用。最小频率指数nmin与临界弹性频率指数nec满足nmin+5≤nec,粗糙球形表面在整个接触过程表现出弹性变形行为。最小频率指数nmin处于临界弹性频率指数nec与临界弹塑性频率指数nepc之间,粗糙表面在初始接触时表现为弹性变形行为,随着接触载荷的增大,逐渐呈现为弹塑性变形行为。当nmin>nepc时,粗糙球形表面在整个接触过程中都呈现非弹性变形行为,这是因为弹性变量形远远小于总变形量。 (2)粗糙球形表面的接触半宽主要取决于基圆半径,微凸体的几何尺寸对其影响很小。当粗糙球形表面处于弹性或弹塑性变形阶段时,接触压力分布曲线近似为抛物线,接触压力在接触区域中心达到最大,向接触区域边缘方向递减。在完全塑性变形阶段,接触压力分布曲线的轮廓近似为矩形,接触压力在整个接触区域上均匀分布。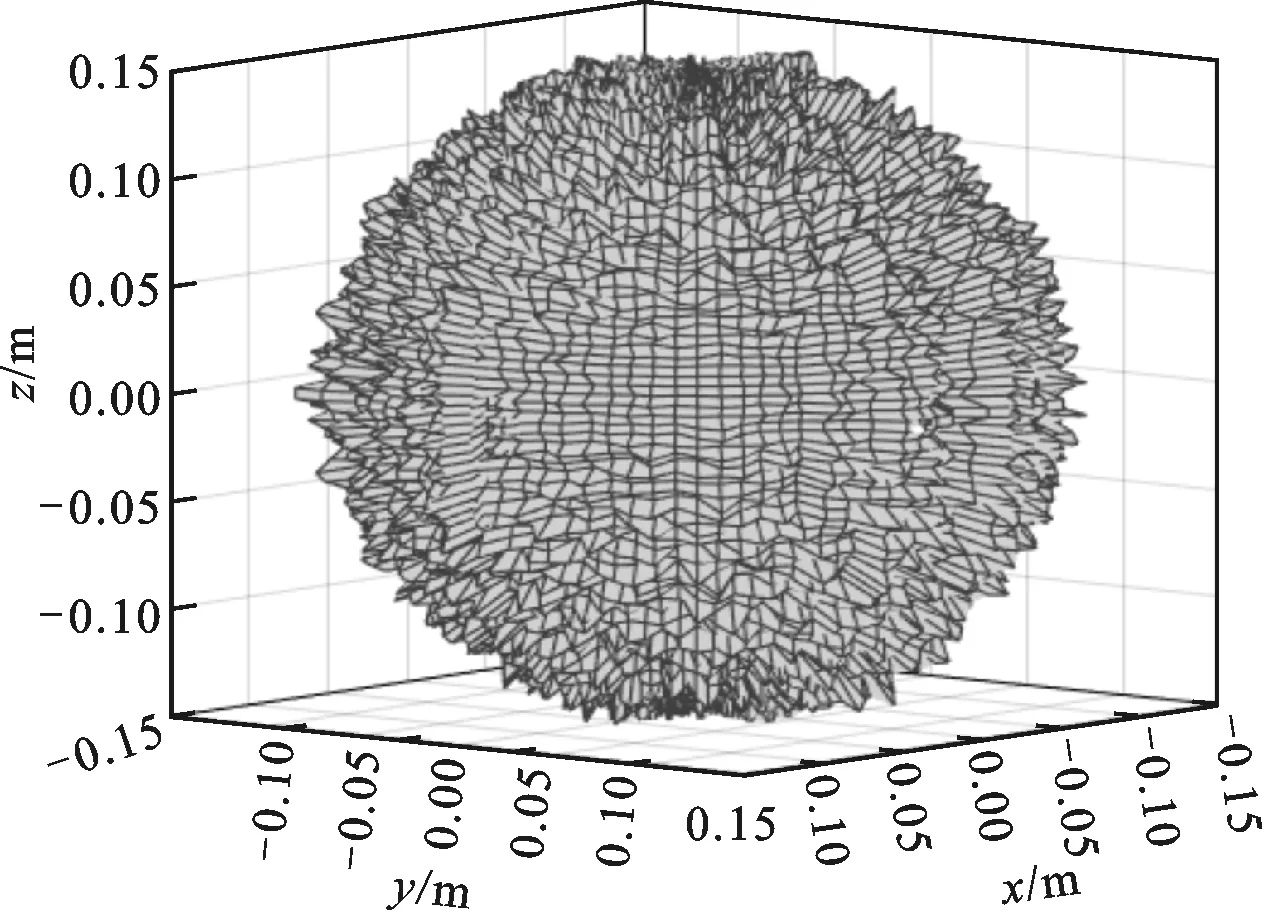
2 单个微凸体的接触力学特性



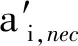
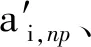
3 真实接触面积和总接触载荷
3.1 接触模型的建立
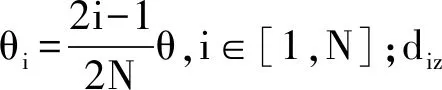
3.2 微凸体的截断面积密度分布函数

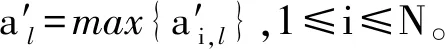
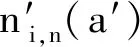
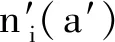

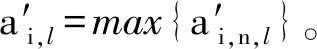
3.3 真实接触面积和总接触载荷
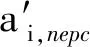
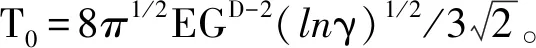
4 计算结果与讨论
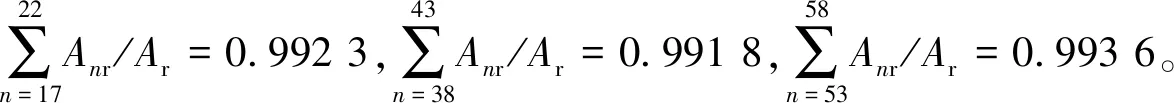



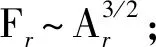

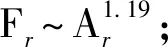



5 结 论