热声旋转发电的数值与实验研究

刘冬冬,陈燕燕,戴巍,罗二仓

(1.中国科学院理化技术研究所,100190,北京;2.中国科学院大学,100049,北京)

热声发动机基于热声效应而工作,是一种新型的外燃式能源转化机械,其热能到声能(机械能的一种)的转换过程无运动部件,结构简单,一般采用惰性气体为工质,具有可利用热源广泛、可靠性高、潜在效率高以及工质环保等优点,在低品位热源利用、分布式发电及独立电源领域有着良好的应用前景[1-2]。为实现热声发电,还需要从声能到电能的转换装置。目前声-电转换环节主要利用直线电机[3-4]实现,声波以压力波动的形式作用在活塞上推动活塞往复振荡,并带动磁体与线圈做相对运动,从而利用电磁感应发电。直线电机采用间隙密封,无油润滑,具有可靠性高、振动小、声-电转换效率高等优点。但是,随着热声发电朝着大功率(百千瓦级电功率及以上)、实用化和经济性方向的发展,直线电机在比功率密度、大尺度间隙密封、大重量支撑技术和成本方面的问题越来越凸显。

为解决大功率声-电转换问题,一种可能的途径就是将气体的往复运动直接通过旋转机械转变成轴功进而带动常规旋转电机发电。旋转运动切割磁力线的速度远大于直线运动,因而比功率显著提升;另一方面,大功率旋转电机发展成熟,经济性较好,因此将声能转换为旋转机械发电在发展经济性、大功率热声发电方面具有较大潜力。事实上,双向透平技术已经在振荡水柱式(OWC)波浪能发电中得到应用[5-7]。例如,中国2001年在广东建成了100 kW的OWC发电装置,2014年澳大利亚MacDonnell港口建成的OWC电站发电功率达到1 MW。在OWC电站中,波浪推动气室中的气体做往复运动,进而推动双向透平单向旋转并带动旋转电机发电,其中固定导流叶片的双向冲击式透平因结构简单、具有较好的变负载特性以及适中的效率而得到更多应用。热声系统中的交变流动虽然与OWC发电中的空气往复流动相似,但OWC中双向透平工作在常压、低频的状态,流体任一方向的流动都接近于稳态流动。这与热声系统中的高压、高频的声学特性显著不同,热声发动机中流体微元的振荡位移相对于透平尺寸来说较小,微元之间通过协同作用,逐步将声功转变为驱动透平的轴功。在OWC波浪能发电站中,以常压下空气为介质的双向冲击式透平发电效率在25%～40%,而在热声发动机的高压、高密度介质中,其工质运行雷诺数可比常压下高近2个数量级,因此热声发电用双向冲击式透平尺寸较之空气透平紧凑许多,功率密度和效率都有望大幅度提高,从而可为热声发电提供一种功率易扩展、经济性好,同时具有中等效率的发电方式。

目前,采用双向冲击式透平进行热声发电的研究刚刚起步,尚处于探索阶段[8-9],缺乏系统的分析方法和实验数据。本文采用稳定来流与可压缩交变来流相结合的方式,优化设计了一套百瓦级定导流叶片的双向冲击式透平结构,并完成了其在常压稳定来流下的输出特性测试,详细考察了其在定转速以及定负载工况下的输出特性变化;同时,通过数值计算与实验的对比,验证了设计分析流程的有效性,并给出了交变来流设计工况下的性能预测,可为进一步在交变流动下对双向透平进行优化与分析提供指导。

1 双向冲击式透平性能分析方法

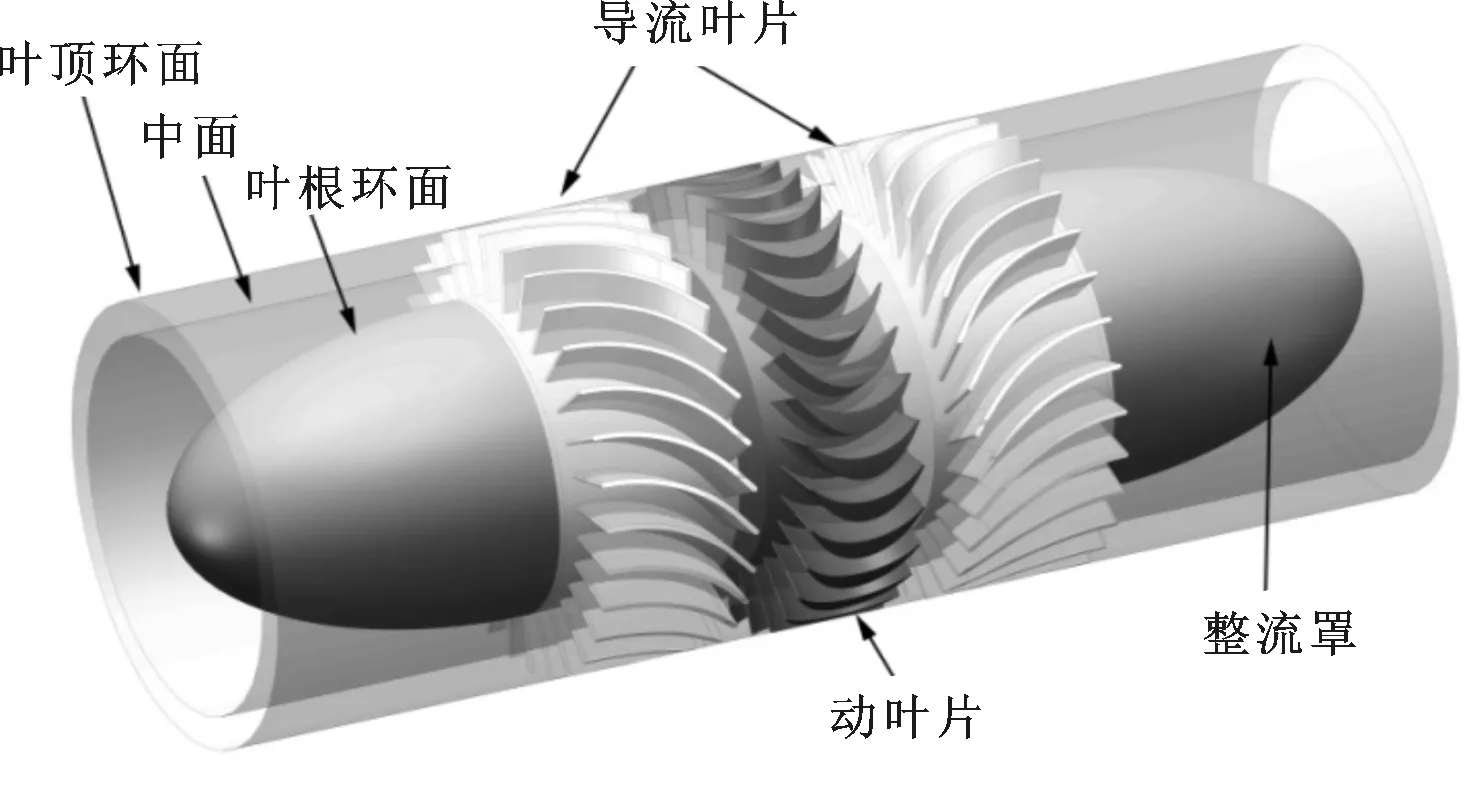
图1 单级双向冲击式透平三维结构

双向冲击式透平由Babintsev于1975年发明[10],如图1所示,透平采用对称结构,往复流动的流体流经导叶后,都向动叶片的弯曲方向冲击,推动叶轮单向旋转。本文所采用的透平动叶片由一段圆弧面与椭圆弧面组成,其中圆弧面迎向流体冲击,称为压力面;椭圆弧面背向流体冲击,称为吸力面。动叶片安装在轮轴上,属于透平的转子部分。导流叶片则采用固定式,为一段圆弧面加一小段与圆弧相切的直线,靠近动叶片处的直线段主要是为了保证将轴向入射气流调整至所需冲击角度。上下游导流叶片以对称方式安装在动叶片两侧的定子上。本文主要采用二维中面分析法对双向冲击式透平性能进行优化分析,该方法可大大简化透平的分析模型,虽然忽略了叶片在径向上的动力差异以及叶顶间隙的影响,但能有效地抓住透平的最基本特征,是透平优化分析中最常用的方法。同时,建立了三维数值模型与实验结果进行对比,并对二维数值模型与实验结果的差异进行分析与校验。

中面法即取动叶片中跨半径处的圆周面展开,如图2所示,得到以动叶片与导叶片外轮廓为壁面边界的周期性重复流道截面。因此,可提取流道最小单元进行分析,单元与单元间的边界则采用周期性边界。本节在常规透平分析方法的基础上引入交变流动特征,介绍交变流动中双向透平特性分析的基本方法。

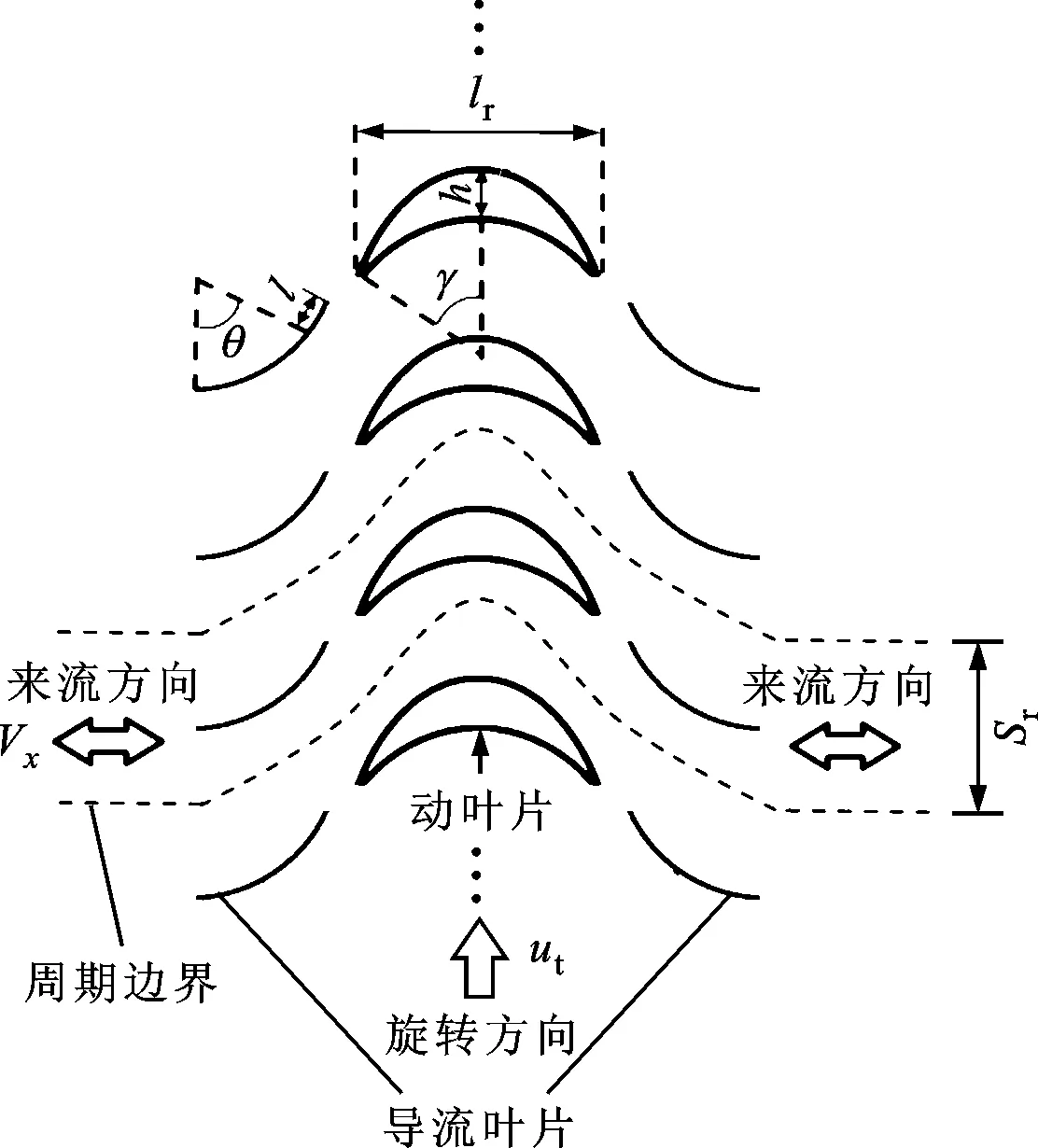
图2 中面流道展开示意图

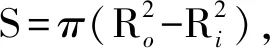
将动叶片在旋转方向上的单位面积合力即升力设为Ft,若忽略叶根至叶顶的差异,透平扭矩M的计算式可写为

(1)

式中r为动叶片微元至旋转轴的距离。对于交变流动,时均透平扭矩的计算中需要采用周期平均升力Ft0。

透平的输出功率Pt为扭矩M与透平旋转角速度ωt的乘积,即

(2)

透平所消耗的能量等于透平两侧流体的总能流之差。对于稳定来流不可压缩流动,当透平进出口截面为等面积且距离透平足够远,从而透平射流及平直流道损失均可忽略时,流体总能流变化只取决于透平两侧压降ΔP与流量VxS的乘积,即

(3)

而对于交变流动,总能流由时均焓流、时均动能及时均黏性力做功组成。热声热机中的交变流动属于低马赫数可压缩流,流场频率f一般为10～100Hz,对于透平流道尺度来说,气体可近似为绝热压缩膨胀过程,因此其时均焓流变化近似等于时均声功流变化。由于透平两侧的时均动能及时均黏性力做功变化均为远小于时均声功的高阶小量而可以忽略,因此交变流动下透平进出口截面的时均总能流变化近似等于声功流之差

(4)

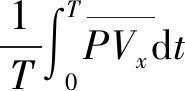
η=Pt/ΔH

(5)

影响透平性能的最主要流场参数是流量系数φ,为来流轴向速度Vx与透平中面旋转速度ut之比,即φ=Vx/ut。在交变流动中,来流速度Vx随时间周期性变化,此时流量系数定义中的来流轴向速度采用等效来流速度

(6)

2 双向冲击式透平的数值模拟

为获得满足性能要求的透平,首先需要对透平的动叶与导叶及其综合性能进行优化设计,为简化计算,优化过程采用二维模型。在获得优化结构后再采用三维模型进行性能校核及与实验结果的对比验证。本文采用商用软件FluentTM对双向透平进行数值模拟,首先在稳定来流下依次优化导流叶片圆弧弯曲角与动叶片,再对整体结构进行交变流动性能分析与局部优化。优化过程重点考察了动叶冲击角θ(近似取动叶冲击角等于导流叶片圆弧弯曲角)、叶片最大厚度h、叶片弦长lr以及动叶片入射角γ的影响。

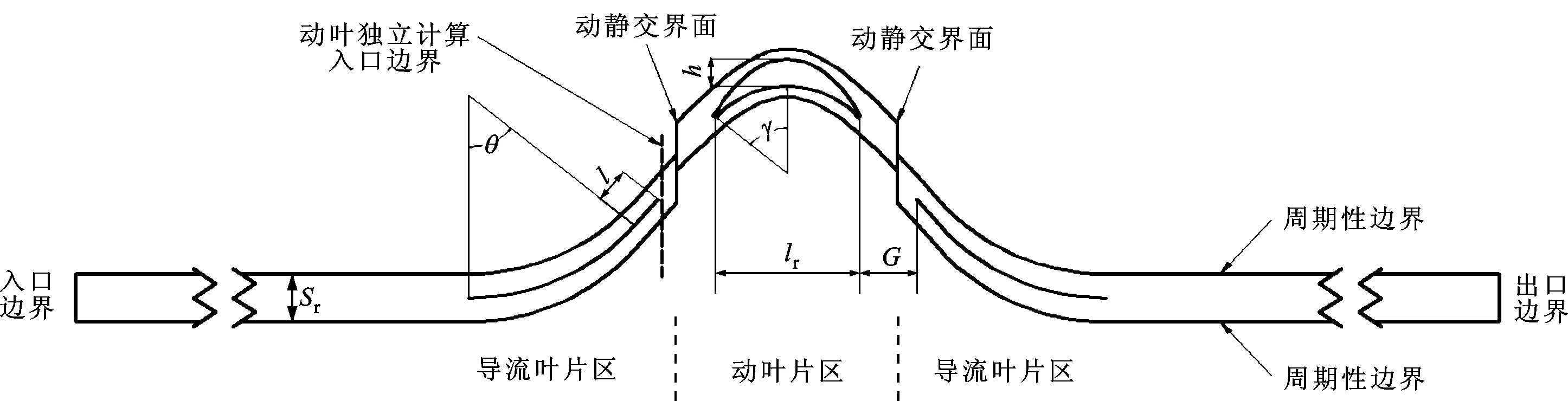
图3 双向冲击式透平二维CFD模型

模型选取中面最小单元进行分析,如图3所示。计算中采用两步法:首先针对动叶进行优化,也是优化的重点;在此基础上再对包含动叶与静叶的完整模型进行优化。第1步的动叶优化采用多参数变工况计算法,为简化起见,采用稳定来流,计算区域只包括上游导叶出口至下游远离叶片的计算区域,不包含下游导流叶片。通过改变动叶冲击角度,即可模拟导流叶片圆弧弯曲角的影响。变化该参数时,可针对动叶的结构参数进行细致考察,从而获得动叶的优化结构及其对应的优化导流叶片圆弧弯曲角。第2步则在第1步的基础上,再对包含两侧导流叶片和动叶片的完整模型进行优化计算,主要优化动叶片与导流叶片间距以及导流叶片直线段长度,从而获得最终的透平结构。

本文只对透平的稳定输出性能进行考察,不包含透平的启动与变工况瞬时特性,因此每个计算工况下给定动叶片转速。动叶片区域使用滑移网格模型处理动叶片的旋转问题并设置交界面来实现转动区域和固定区域的数据传递,因此稳定来流时,同样需要采用瞬态计算模型;流场周期界面设置为周期性边界;叶片边壁为无滑移壁面;湍流模型采用k-ε模型;压力的空间离散采用PRESTO!;动量的空间离散采用二阶迎风格式,时间离散采用二阶隐式方法。稳定来流计算时,进、出口边界分别采用速度入口、压力出口。交变可压缩来流计算时,进口边界采用位移定义的活塞动网格边界,出口采用压力边界,二者均为随时间变化的函数;工作介质采用可压缩理想气体模型。模型中叶片附面边界层采用结构化网格,边界以外采用三角形非结构化网格;叶片以外的前后来流区域则采用结构化网格。通过网格无关性检验计算后,取附面边界层最小厚度为0.05 mm,边界层以外主流区域网格尺度为0.5 mm,各模型网格总数均在7万左右。时间步长的最高要求来源于动、静交界面滑移网格数据传递精度的影响,计算中取每时间步长网格滑移量小于等于二分之一界面网格尺度。以转速n=3 000 r/min为例,时间步长小到每旋转周期的1/1 000,该设置满足时间步长无关性检验要求。

根据百瓦输出需求并考虑与常规热声系统的耦合,设计工况转速为3 000 r/min,工作介质选为6 MPa的氦气,叶片外径为80 mm,借鉴OWC常规设计,轮毂比选为0.7,叶片数选为30,因此叶片螺距为7.12 mm。图4～图6给出了动叶尺寸对输出功率及透平效率的影响规律,同时给出了固定透平尺寸下动叶冲击角θ对透平性能的影响。可以看出:动叶参数的变化不影响动叶冲击角对透平性能的基本影响规律,透平功率与效率均存在最优的动叶冲击角,但二者对应的最优角相差较大。功率对应的最优动叶冲击角在20°附近,而效率对应的最优动叶冲击角则在7°附近;另一方面,减小动叶厚度、增大动叶弦长或减小动叶入射角均能使两个最优动叶冲击角相互接近,但是接近的程度均非常有限。这一规律反映了双向透平的设计难以同时兼顾输出功率与透平轴功转换效率。因此,根据百瓦级功率需求及效率不低于60%的设计要求,折中考虑透平的输出功率和效率,在效率尽可能高,而输出功率余量较大的情况下,选择动叶冲击角为50°,对应的入流最佳导流叶片圆弧弯曲角应稍大于50°,但出流时又要求导流叶片圆弧弯曲角小于动叶冲击角以减小阻力,因此取导流叶片圆弧弯曲角等于动叶冲击角。

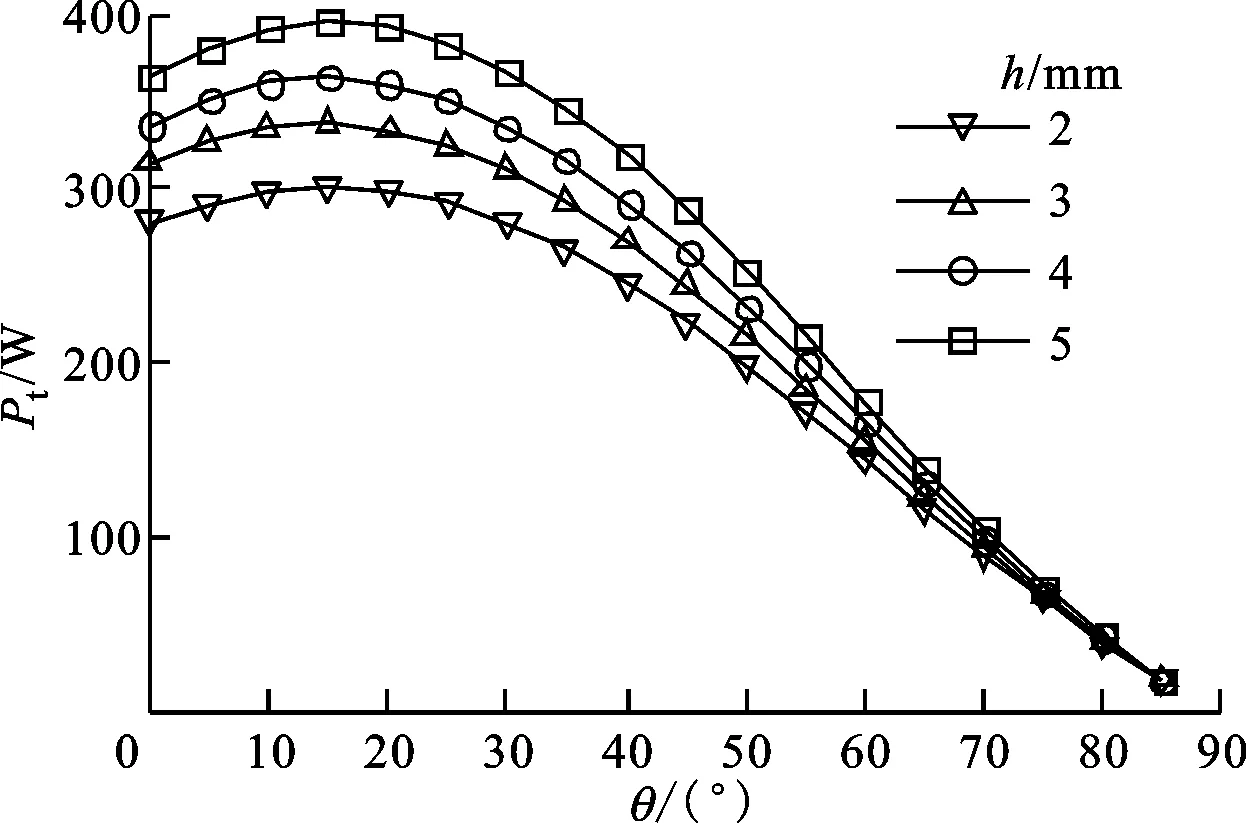
(a)不同h下Pt随θ的变化

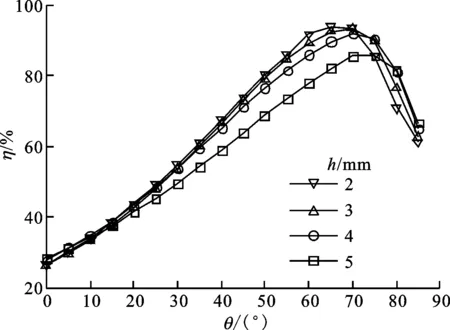
(b)不同h下η随θ的变化图4 动叶片最大厚度对透平输出特性的影响(lr=20 mm,γ=50°,φ=3)

对于动叶结构参数的影响方面,图4给出了动叶片的最大厚度从2 mm变化到5 mm时的影响,结果显示增加叶片厚度能明显增加透平输出功率,效率略有下降,但最大厚度大于4 mm后,效率下降明显,因此叶片最大厚度选为4 mm。图5给出了动叶片弦长从10 mm变化到50 mm时的影响,可以看出在一定弦长范围内,动叶片越短,最大输出功率越大,但当弦长过短,例如10 mm时,动叶片尾部在60°附近出现了卡门涡街,流动损失显著增加,导致其效率突降,因此选择叶片弦长为20 mm。图6给出了动叶片入射角从50°变化到70°时的影响,入射角越大表示动叶片弯曲弧度越大,输出功率越大,而最大效率变化不大。当选择导流叶片圆弧弯曲角θ为50°时,γ越大效率下降越明显,因此择优选择效率后,同时满足功率要求,动叶片入射角γ也选为50°。

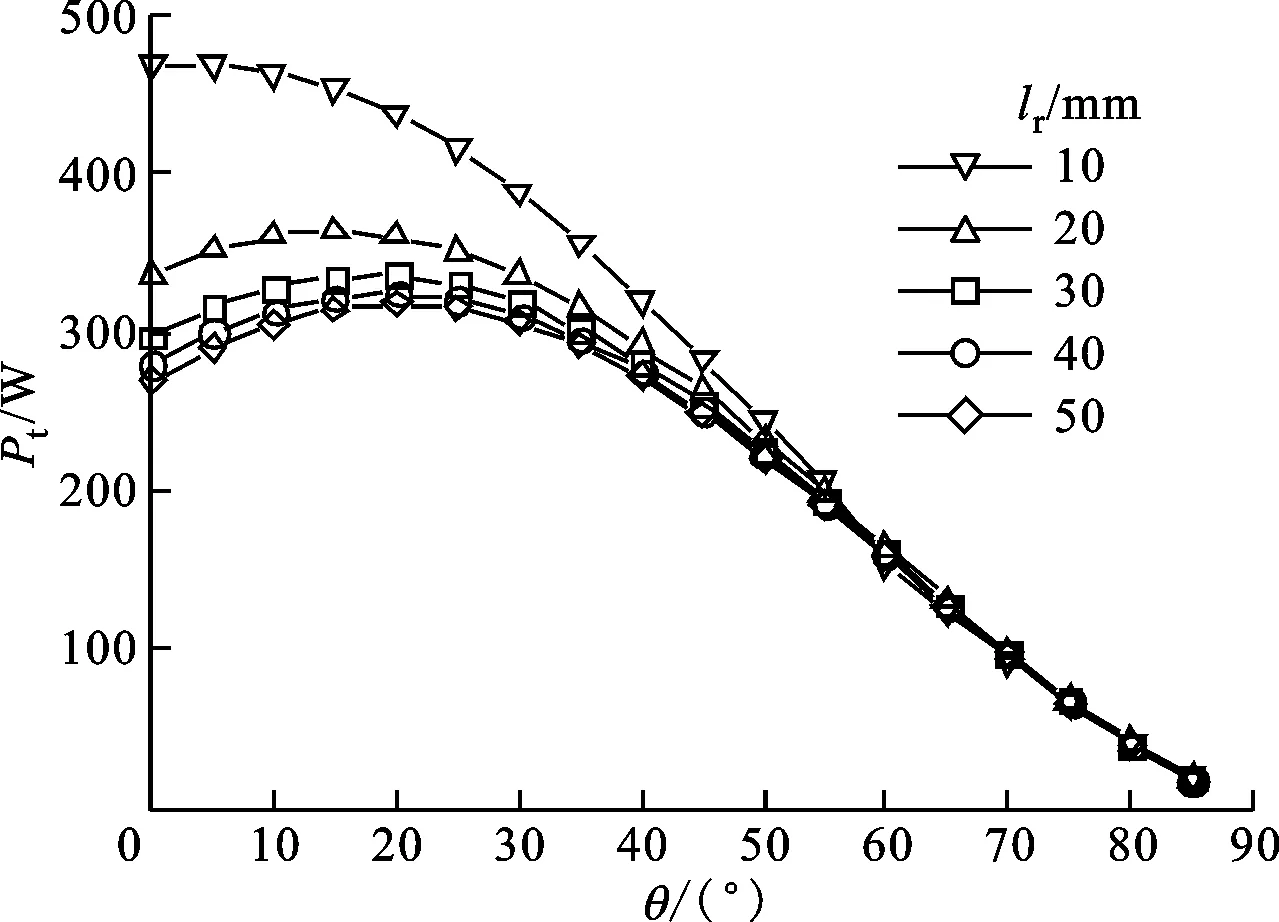
(a)不同lr下Pt随θ的变化

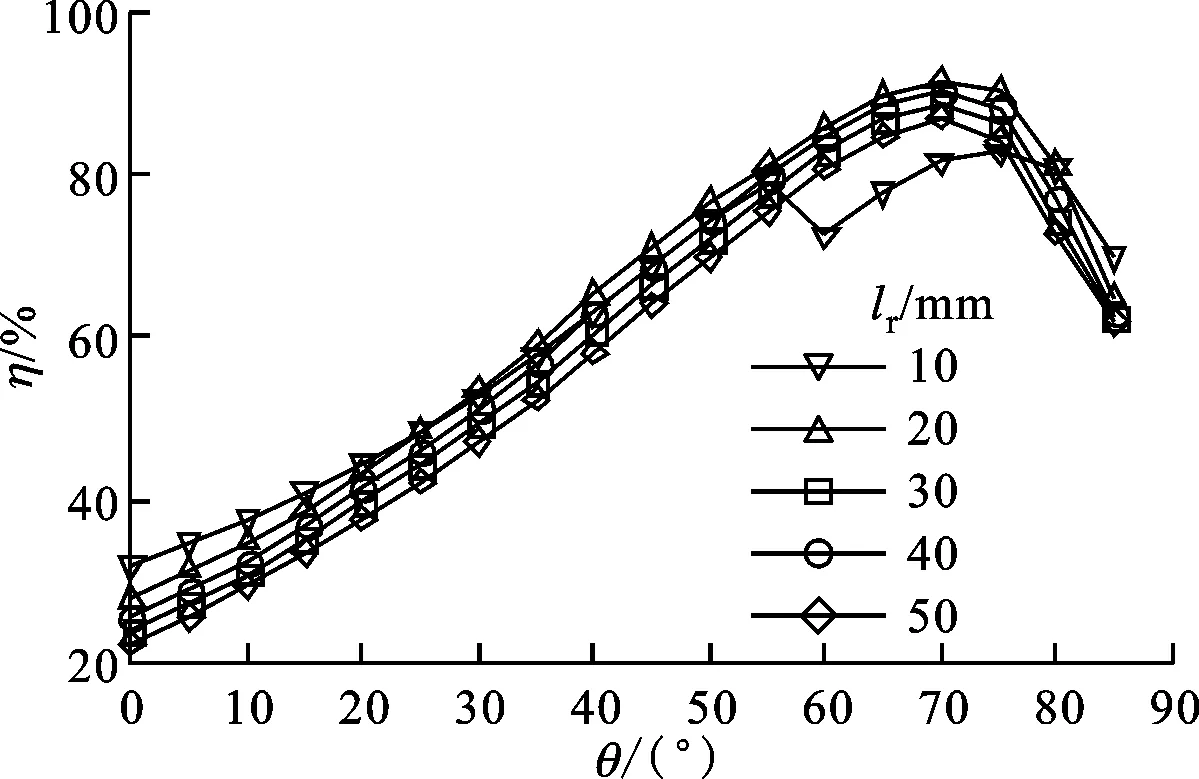
(b)不同lr下η随θ的变化图5 动叶片弦长对透平输出特性的影响(h=4 mm,γ=50°,φ=3)

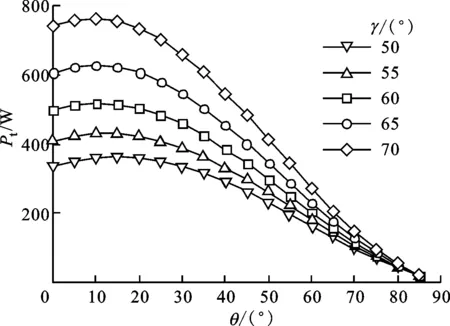
(a)不同γ下Pt随θ的变化

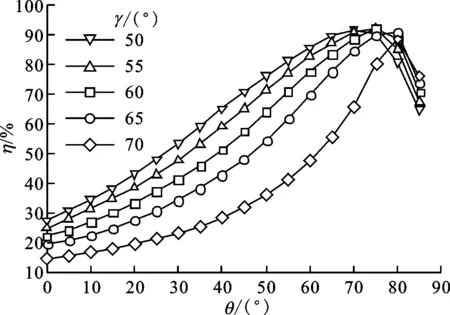
(b)不同γ下η随θ的变化图6 动叶片入射角对透平输出特性的影响(lr=20 mm,h=4 mm,φ=3)

根据以上优化分析,确定了透平总体结构以及对系统性能影响最为关键的动叶片结构参数与导流叶片弯曲角;再通过对图3所示包含动叶与导流叶片的完整模型进行稳定来流与交变来流下的数值模拟,同时对其他透平参数进行小范围优化以及透平整体性能核算,最终获得的透平结构参数列于表1。

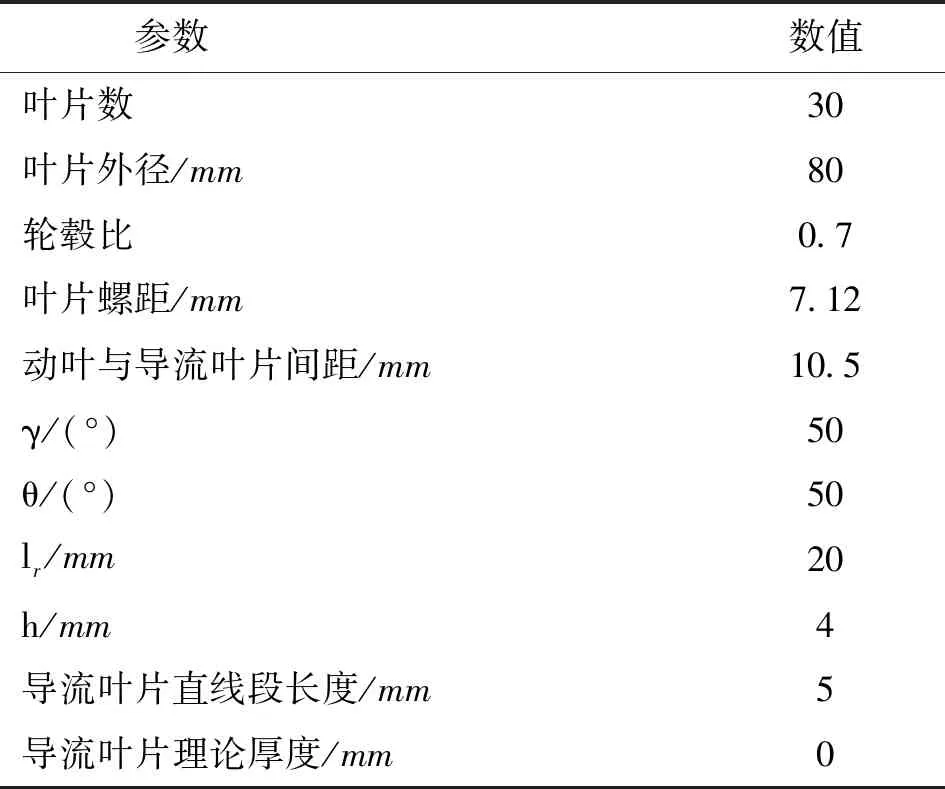
表1 双向冲击式透平结构参数

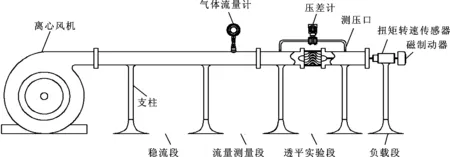
图8 双向透平稳定来流实验测试装置

图7给出了优化后透平以3 000r/min的转速在稳定来流与交变流动条件下的输出特性。从图7a可以看出,输出功率随流量系数的增加显著增加,但频率对输出功率几乎无影响,因此交变流动下采用等效速度计算式(6)定义的流量系数与稳定流动下的流量系数是等效的。从图7b中稳定来流效率随流量系数的变化中可以看出,存在最优流量系数使得透平效率最高,但交变流动下的透平效率明显降低,频率越高效率越低,且效率对应的最佳流量系数较稳定来流小。

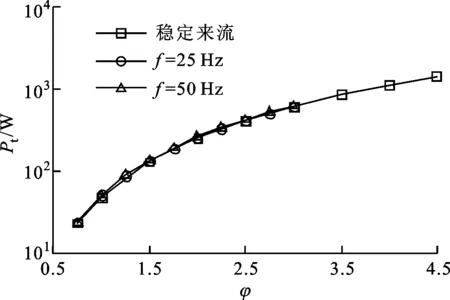
(a)Pt随φ的变化

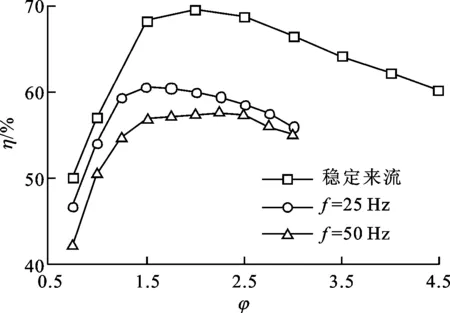
(b)η随φ的变化图7 稳定与交变来流工况下双向冲击式透平的输出特性

3 实验系统与透平稳定来流特性测量

根据表1结构参数,采用3D打印技术制作了材质为光敏树脂的双向透平,导流叶片厚度理论值为0,但实际加工时存在有限厚度,测得实际打印的导流叶片最大厚度为1mm;同时动叶旋转要求叶片顶端留有有限间隙,测得实际叶顶间隙为0.2mm。透平稳定来流下的输出性能测量实验装置如图8所示。

实验装置主要由离心风机、稳流段、流量测量段、透平实验段和负载段,以及数据采集设备等组成,其中离心风机采用变频电机驱动,通过控制风机的转速调节流量大小。进口气流速度由热式气体流量计测量。在透平前后等距设置测压口,气体流经透平前后的压降由JYB-D3151型单晶硅压差计测得,精度为±0.075%。透平输出的扭矩和转速由YH502型扭矩转速传感器测量,精度为0.5%。透平的负载由HB-1M型磁制动器通过输入的磁滞电流控制。

实验考察了透平在定转速以及定负载工况下的输出特性变化,在定转速实验中,为保持透平转速不变,通过调节磁滞电流来获得所需转速,再通过改变来流速度实现不同流量系数下的透平定转速输出性能实验。在定负载实验中,保持磁滞电流不变,通过改变来流速度实现不同工况下的定负载实验。透平输出功率计算中忽略磁制动器的损失。

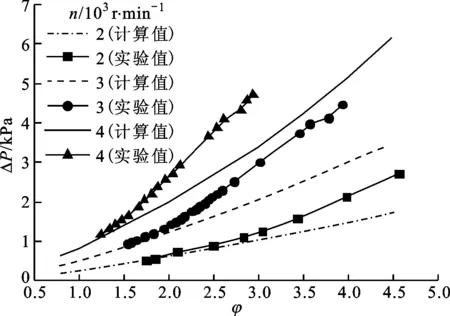
(a)不同转速下ΔP随φ的变化

(b)不同转速下Pt随φ的变化

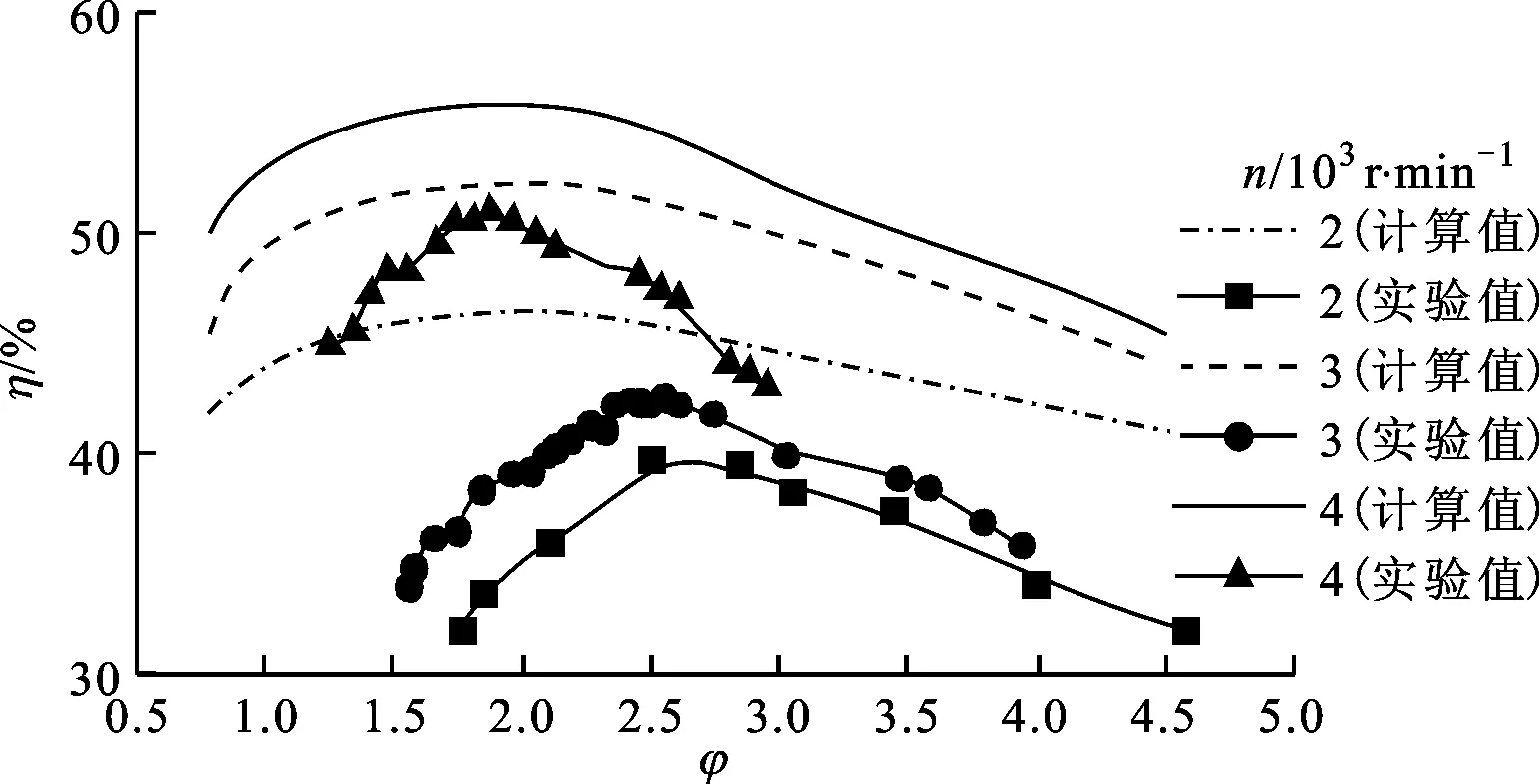
(c)不同转速下η随φ的变化图9 不同转速下双向透平性能实验与计算结果

图9给出了在保持双向透平转速为2 000、3 000、4 000r/min时透平两侧压降、透平输出功率以及效率随流量系数的变化,同时给出了透平在与实验相同进、出口及转速工况下的二维计算结果。从各特性参数随流量系数的变化中可以看出,计算结果与实验测量结果趋势上符合较好,但数值上随着转速增加,流量系数增大时偏差明显增大,其中输出功率的计算差异相对较小,但效率间的差异较为明显,说明二维计算对透平损失的模拟存在较大误差。在透平的输出性能方面,透平转速越高,相同流量系数下输出功率与效率均越高。实验在转速为4 000r/min、流量系数为1.9时获得输出功率83W,透平效率为51%。

图10为定负载时双向透平实验性能测量结果及与二维计算结果的对比,其中透平的负载采用输入磁制动器的磁滞电流表示。实验中采用的磁滞电流I分别为0.08、0.10、0.12、0.15A,系统在转速为5 250r/min时测得最大输出功率为230W,对应效率为44.4%。由图10c可以看出,在负载一定时,随转速升高,透平效率计算值的增加逐渐平缓,而实验值在4 000r/min时达到峰值,随后有下降趋势。随负载增大,不同转速下透平的输出功率以及透平压降的实验与计算值偏差也愈加明显。

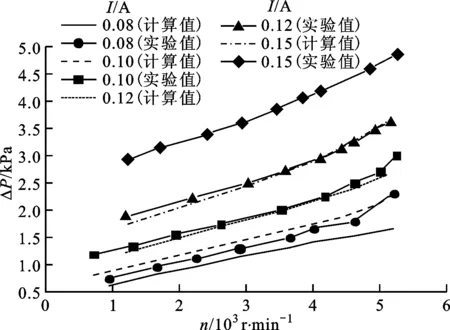
(a)不同负载下ΔP随n的变化

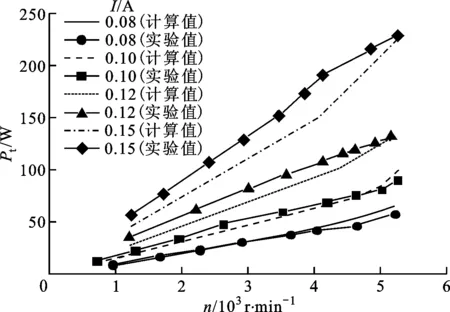
(b)不同负载下Pt随n的变化

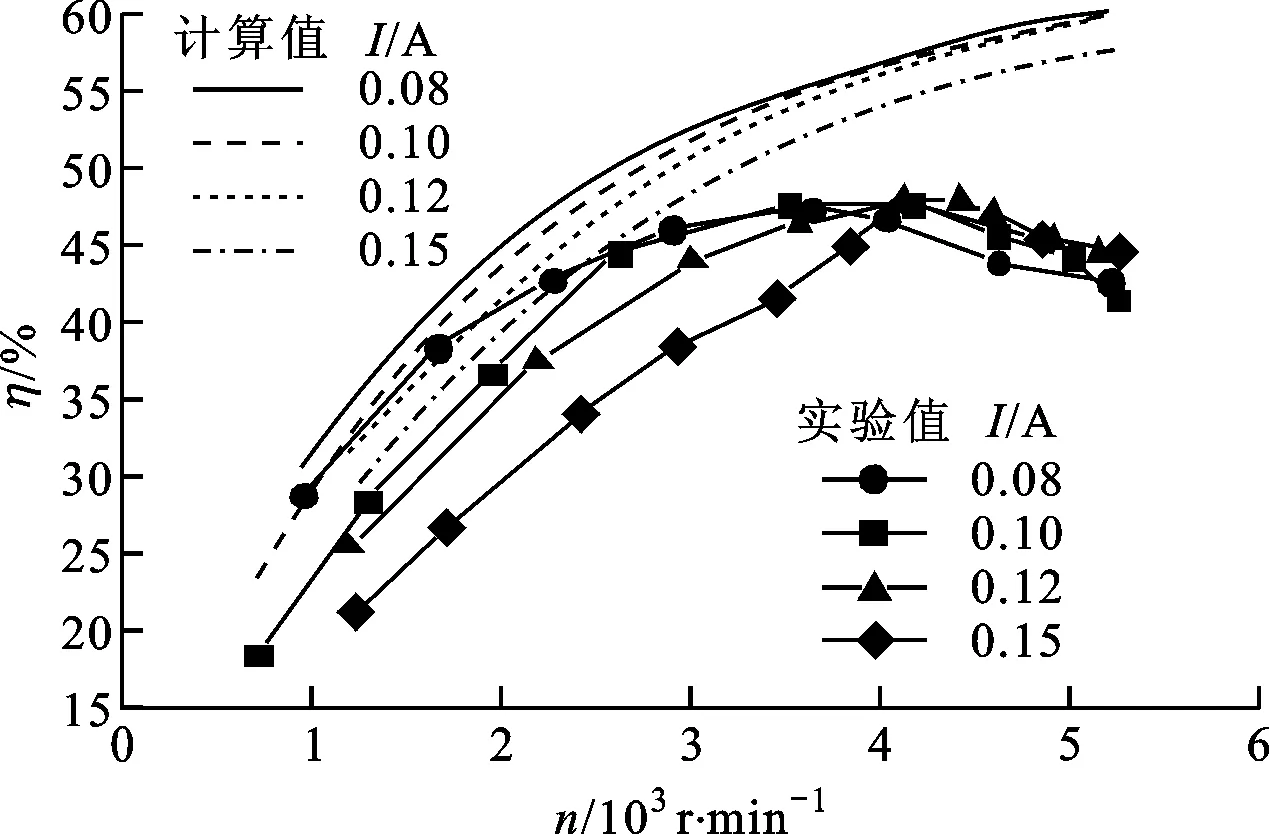
(c)不同负载下η随n的变化图10 不同负载下双向透平性能实验与计算结果

4 模型比较与交变来流下的性能预测

二维模型对于多参数、多工况计算在计算速度和数据分析上具有优势,但从以上计算对比看出,在定量上还存在较大差异,特别是随着功率密度增加,在效率预测上的精度较差。二维计算与实验差异的主要来源有两个,首先是二维模型中无法计入叶片径向上转速变化产生的影响,其次二维模型中没有考虑到叶顶间隙的损失。为检验这一影响,对实验透平进行了三维建模计算,其中三维模型的计算设置以及计算区域的网格划分原则与二维相同,只是在径向上进行了三维结构化延伸,总网格数达到100万,如图11所示。图12给出了转速为3 000 r/min时,不同流量系数下实验、二维计算以及三维计算的结果,三维计算中的叶顶间隙(δ)分别为0、0.2 mm。

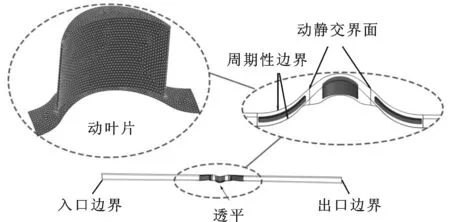
图11 双向冲击式透平三维CFD模型

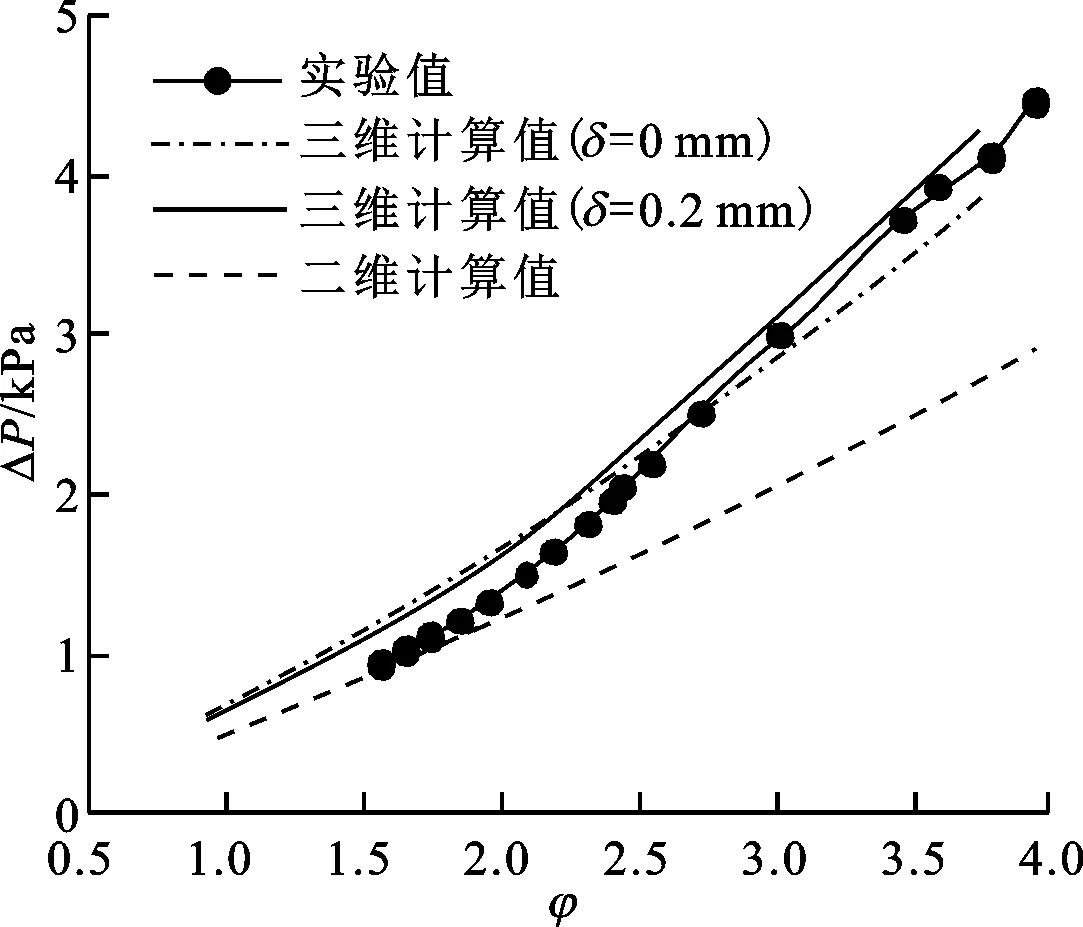
(a)压差的对比

(b)功率的对比

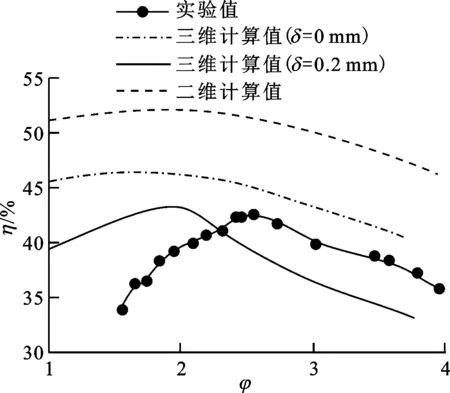
(c)转换效率的对比图12 二维、三维模型参数计算值与实验值的对比

从各性能参数随流量系数的变化可以看出,三维模型对于透平两侧压差的计算可以很好地与实验结果吻合,但对于输出功率的计算,三维模型与二维模型相近,均与实验结果有一定偏差,且功率越大,计算值越小于实验值,不排除一部分原因来自于实验负载测量与实际轴功之间的误差。输出功率的差异直接导致三维计算模型与实验结果在透平转换效率上的差异,二者最高效率与变化规律虽然相似,但最佳效率对应的流量系数计算结果向小流量系数偏移。图12还给出了有无叶顶间隙情况下的计算效率对比,其差异水平及与二维数值计算的对比说明,叶顶间隙为0.2 mm的叶顶泄漏损失与径向分布特性对效率的影响程度相当。

图13给出了透平以3 000 r/min的转速在频率为25 Hz的6 MPa氦气交变来流下工作的性能预测。从图中可以看出,输出功率随流量系数增加显著增加,而效率在流量系数为1.25时取得极大值40%,此时输出功率为101 W。

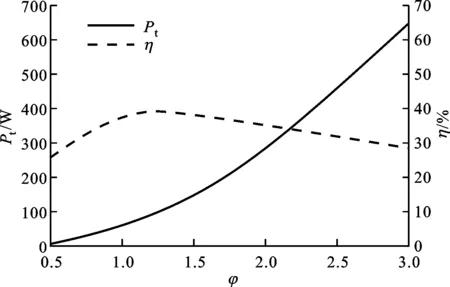
图13 交变来流工况下的透平输出特性预测

5 结 论

本文采用稳定来流与可压缩交变来流相结合的方式,利用CFD模型优化设计了一套百瓦级定导流叶片的双向冲击式透平结构,实验完成了其在常压稳定来流下的输出特性测试,考察了其在定转速以及定负载工况下透平的输出特性变化。实验获得透平最大输出功率为230 W(转速5 250 r/min,对应效率为44.4%),最大透平效率为51%(转速4 000 r/min,对应输出功率为83 W,流量系数为1.9)。将实验值与计算值进行了对比,结果表明二维计算值定量上与实验值存在明显差异,但对系统性能的预测仍具有指导意义;三维计算弥补了二维计算的不足,计入了叶片径向旋转速度差异以及叶顶泄漏的影响,与实验结果符合良好,但二者输出功率上的差异仍需要结合不同的轴功测量手段做进一步的检验与分析。基于三维模拟给出了透平在交变流动下的性能预测,透平以3 000 r/min的转速在频率为25 Hz的交变来流下的最大效率达40%,此时输出功率为101 W。