氢原子对非对称Σ5晶界α-铁力学性能影响的模拟研究

许天旱， 赵典典， 宋海洋

(西安石油大学 材料科学与工程学院，西安 710065)

1 引 言

众所周知，金属材料中的氢脆(HE)是导致材料丧失延展性从而使其变脆的现象.这在工程应用中常常引发很多重大的事故.因此，多年来它始终是人们研究的焦点[1]，但其潜在的机制及其与金属之间的相互依赖关系仍不清楚.目前为止，实验中已经确定的主要机制是氢化物的形成和断裂、氢降低原子间结合力(HEDE)、氢增强局部可塑性(HELP)和吸附诱导位错发射(AIDE)[2].氢原子半径小，很容易在金属晶格中迅速扩散，并会被金属中的各种缺陷所捕获，如晶界(GB).晶界的氢偏析对位错在晶界之间的滑移、迁移起着重要作用[3]，最终导致了材料晶间断裂.另一方面，晶界的氢偏析也可能对材料的塑性变形机制产生显著影响，如晶界滑移和迁移、孪晶和位错的发射[4,5].由于氢原子的存在会对材料性能产生严重的影响，因此了解它们与晶界之间的相互作用对未来材料的设计至关重要.

尽管计算和实验研究方面已经揭示了晶界特征如何影响点缺陷的吸收和有害原子的扩散，但其中许多双晶模拟集中在对称倾斜晶界上.我国学者沈海军等人[6]研究了铝单晶、双晶及其含氢模型在拉伸条件下的力学特性，研究表明：和同等条件下的铝单晶相比，铝双晶氢脆破坏更为敏感.Zhou等人[7]计算研究了面心立方金属Ni，Cu，γ-Fe和Pd在对称晶界处的氢吸附，发现了晶界间隙氢吸附能量变化的化学机理.方淑娟等人[8]研究了氢在面心立方金属Ni Σ3和Σ5对称晶界的偏析及其相互作用.计算表明，氢原子在Σ5晶界上有明显的偏析行为.然而实验表明，多晶材料中的大多数边界是非对称倾斜晶界(ATGB).因此，研究ATGB以最大限度地发挥工程晶界的优势是非常重要的.此外值得注意的是，迄今为止大多数双晶体的原子模拟还主要致力于研究面心立方(FCC)体系，而具有更复杂的塑性变形机制的体心立方(BCC)金属材料的研究仍然较少，特别是含非对称倾斜晶界的BCC晶体材料在氢环境中的塑性变形机制的研究.

由于晶界复杂的局部原子结构以及氢的多种扩散路径，实验在评估晶界附近的氢扩散方面往往受到很大的限制.然而，经典的分子动力学(MD)[9-11]可以更多地提供有关氢与晶界结构之间复杂的内在关系.在本文中，我们选择含有非对称Σ5晶界的α-铁作为研究对象，采用分子动力学模拟方法研究了晶界旋转角和氢原子浓度对双晶α-铁力学响应的影响.

2 模拟方法

模拟中选取具有Σ5晶界的双晶α-铁为研究对象，双晶α-铁是由上下两个晶粒相对于彼此以一定的角度(θ1，θ2)旋转获得的，晶粒间的夹角为固定的φ=θ1+θ2=36.86°[12]，如图1(a)所示.晶界平面围绕轴线[100]的旋转角用φ来表示.本文通过控制θ1，θ2的大小来改变Σ5晶界的旋转角φ，当θ1≠θ2时，模型则呈现非对称倾斜晶界.为了研究含有非对称倾斜晶界的双晶α-铁的力学行为，我们构建了四个Σ5非对称倾斜晶界(ATGB)，旋转角度φ分别为11.31°、26.57°、30.96°和36.86°.对于含氢的模型，氢原子均匀地分布在晶体中，如图1(b)所示.模拟中所有模型尺寸(X×Y×Z)均为1.7 nm×9.1 nm×13.7 nm.

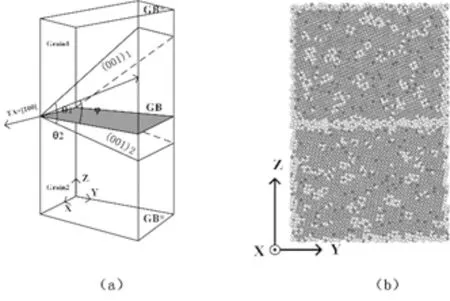
图1 (a)具有Σ5非对称倾斜晶界的双晶α-铁的示意图.θ1、θ2分别为上下两个晶粒的(001)面与晶界的夹角.φ为晶界平面旋转角；(b)旋转角度φ为36.86°，氢浓度为2.2%的原子结构图Fig. 1 (a)Schematic view of a bi-crystal α-iron with Σ5 asymmetric tilt grain boundary. θ1 and θ2 are the angles between the of the upper and lower grains of (001) plane and grain boundary, respectively. φ is the rotation angle of plane boundary; (b) Atomic structures with hydrogen concentration of 2.2% and the rotation angle φ=36.86°

在模拟中，沿X方向和Z方向施加周期性边界条件，Y方向使用自由边界条件.这就产生了具有镜面相同结构的两个周期性的晶界；一个位于计算单元的中间(标记为GB)，另一个位于单元格边界的下方或上方(GB*).在载荷过程中，沿着Z轴方向进行位移加载.模拟过程为：先对初始模型进行15,000步的弛豫，使之能量最小化；接着在Z方向上施加0.001的拉伸应变，然后系统弛豫2000步以释放多余的应力使之回到平衡态.重复对模型施加位移载荷、弛豫，使之处于准静态受力状态.时间步长为1 fs.模拟在300 K下进行，以捕捉室温下的变形机制.为了便于分析系统在拉伸过程中的各种变形机制，通过公共近邻分析(CNA)方法根据原子的局部晶体结构对原子进行着色.这些都是在可视化工具(ovito)中实现的.其中，蓝色原子、绿色原子和白色原子分别代表BCC结构、FCC结构和其他存在于界面或位错处的原子.

在研究中，采用Ackland[13]提出的嵌入原子法(EAM)势来描述铁原子间的相互作用.铁和氢原子相互作用则采用Ramasubramaniam[14,15]和Song[16]等人提出的半经验EAM势来描述.该势函数已被广泛用来研究金属铁的相变、氢和位错核的相互作用以及氢脆方面的力学行为[17,18].

3 结果和讨论

为了研究旋转角度φ对双晶α-铁力学行为的影响，图2给出了不同φ值下非对称倾斜晶界的双晶α-铁在单轴加载下的应力-应变曲线.从图2可以看出，在不同旋转角度下，拉伸的初始阶段都经历了弹性形变的过程.随着应变的增加，应力到达一个峰值.从图中可以发现峰值应力随着旋转角度的变化呈现“折线形”排布.这是由于旋转角度导致的界面结构的差异[19,20].从图中还可以看出，峰值应力下降时所对应的应变几乎不依赖于晶界旋转角度.应力达到峰值点以后，模型进入塑性阶段.从应力应变曲线来看，在塑性阶段对于所研究模型来说，随着应变的增加，应力出现了下降随即又上升的现象.

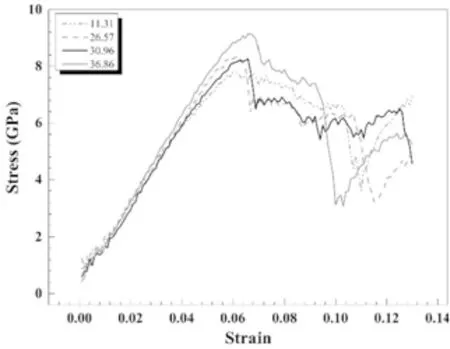
图2 不同旋转角度下的双晶α-铁在单轴加载下的应力-应变曲线Fig. 2 Stress-strain curves of bi-crystal α -iron under uniaxial loading at different rotation angles

为了探究曲线变化的原因，图3给出了26.57°模型在峰值点(ε=0.064)、峰值点之后(ε=0.08)和曲线骤降(ε=0.111)时不同应变下的原子结构图.图3(d-f)给出了不同应变下的局部原子结构放大图.从图3(a)中可以看出在峰值点处，从晶界产生的FCC相开始扩展，应力得到释放，峰值应力下降，最终导致沿着施加载荷的～45°方向形成剪切带.然而，该FCC相是亚稳态的，从图3(c)可以看出，随着应力的继续加载，FCC相出现退化，FCC原子逐步转化成BCC原子，这也就是应力应变曲线第二次出现骤降的原因.骤降到最低点，FCC相完全转变为BCC相，应力应变曲线随即上升.

图3 (a-c)26.57°模型在应变为0.064、0.08、0.111时的原子结构图；(d-f)分别为(a-c)图中方框区域的放大图Fig. 3 (a-c) Atomic structure of the 26.57° model at strains of 0.064, 0.08, and 0.111; (d-f) Magnifications of the block region in the (a-c) diagrams

图3表明，在双晶α-铁中，通过两步法实现相变和所得的晶体重新取向.最初，双晶α-铁具有完美的[100] -BCC晶格(如图3(a)和(d)所示).在应力作用下，弹性剪切应变的积累导致[100] -BCC晶格转变为FCC相.随着应力加载，FCC相转变为新[111] -BCC相，如图3(f)所示.另外，从图3(a)和(b)中还可以看出，对于非对称晶界的双晶α-铁，相变的产生相对于晶界是不对称的.这是因为非对称晶界上每一侧的晶粒相对于拉伸应力方向取向不同，导致其拥有不同的Schmid因子.因此，滑移系可以很容易地在具有较高Schmid因子的晶粒中活化，因为该晶粒中的滑移系具有更高的分剪切应力.

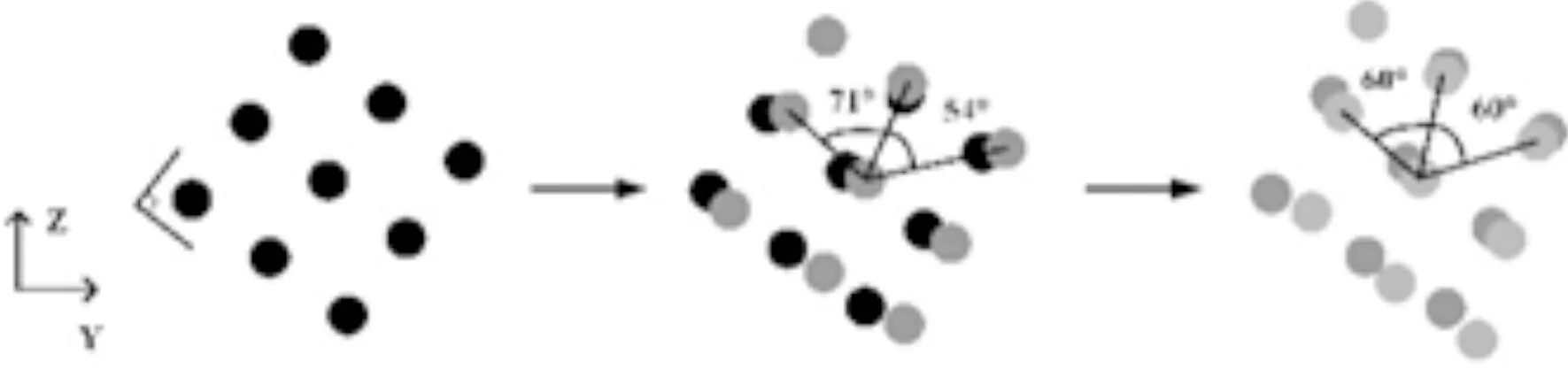
图4 相变过程中的原子结构变化示意图Fig. 4 Schematic diagram of atomic structure changes during phase transition

图4给出了相变过程中的原子结构变化示意图.可以看出，连续拉伸载荷导致特征化的面间角首先从[100] -Fe中的90°减小到71°(在FCC阶段中表征的面间角)，然后又转变成[111] -Fe中的60°，该过程实现了BCC相向FCC相，再向新BCC相的转变[21].原子分析表明，FCC相存在于相界的前面，并作为后续相变的前体.随着相界的逐渐延伸，双晶α-铁的塑性变形主要通过BCC相向FCC相，再向新BCC相的转变进行.

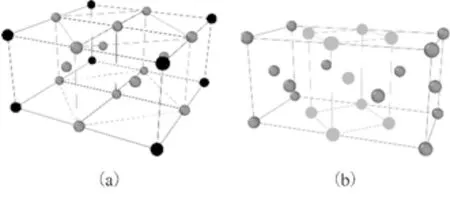
图5 (a)BCC晶格向FCC晶格的转变路径；(b)FCC晶格向BCC晶格的转变路径Fig. 5 Transition paths of (a) BCC lattice to FCC lattice and (b) FCC lattice to BCC lattice

为了研究氢浓度对非对称倾斜晶界双晶α-铁机械性能的影响，我们选择36.86°模型为研究对象，在晶体内部均匀加氢.氢浓度定义为氢原子数除以总的原子数.氢浓度是基于我们以前的研究所决定的[22].这里，氢浓度范围为0.0%至2.2%.值得注意的是，本文中氢浓度比实验中的氢浓度高.这是因为氢原子在晶体中的扩散是长距离的运动，而且在室温下，氢原子和晶格缺陷的协同运动比较缓慢[23].由于低浓度扩散在分子动力学模拟过程中需要很长时间，因此为了提升计算速度，大多数研究采用人为的高浓度的加氢方式[18, 24].

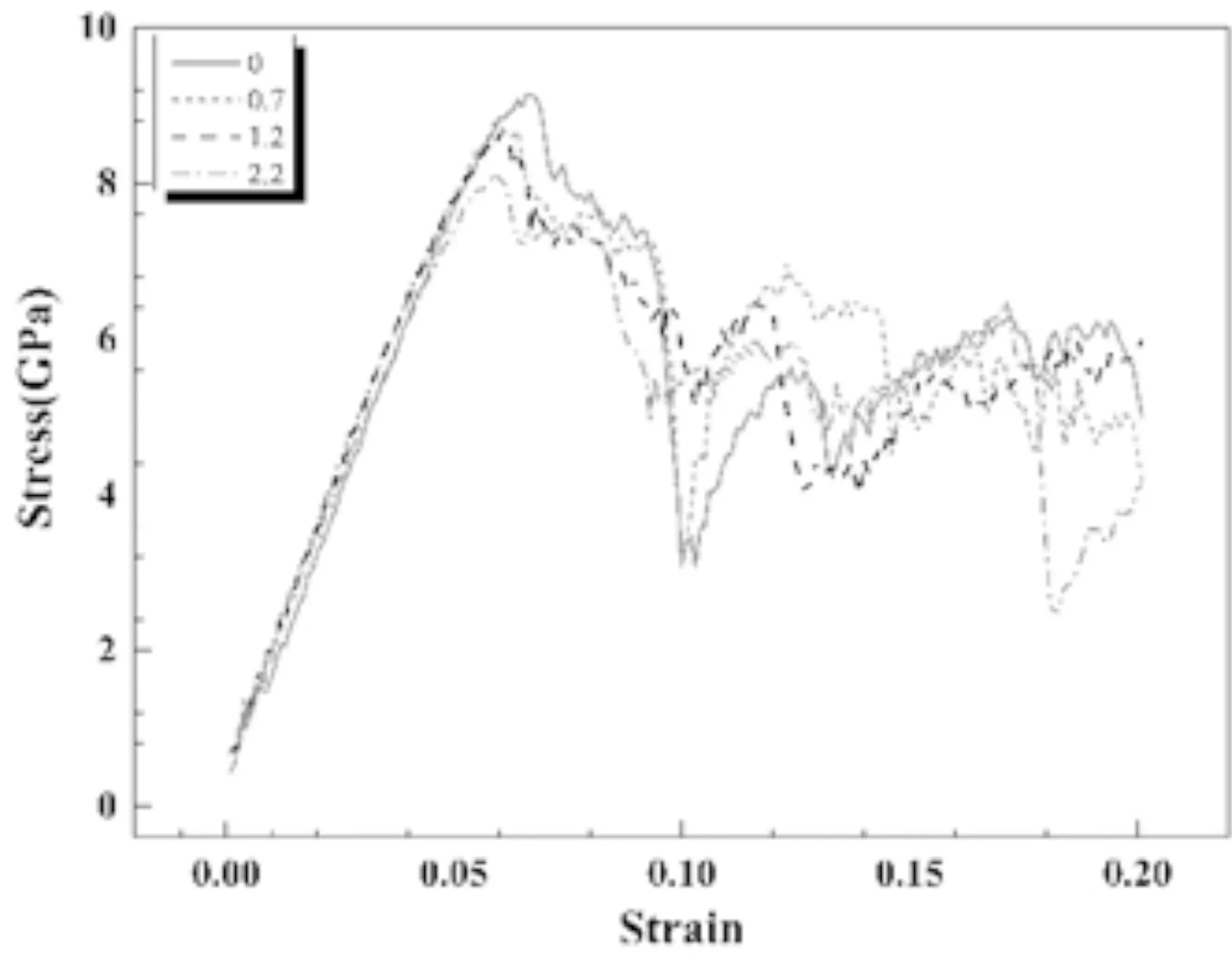
图6 不同氢浓度下的双晶α-铁在单轴加载下的应力-应变曲线Fig. 6 Stress-strain curves of bi-crystal α -iron under uniaxial loading at different hydrogen concentrations

图6给出了不同氢浓度的36.86°双晶α-铁在单轴加载下的应力-应变曲线.可以看出，在弹性阶段，随着氢浓度的增加，杨氏模量有些许降低，在氢浓度为2.2%时较为明显.这是因为氢原子存在于晶体间隙位置，导致相邻的Fe原子之间的结合强度减弱.另外，峰值应力也随着氢浓度的增加而降低，且氢浓度越大峰值应力降低程度越大.这是由于随着氢浓度的增加，间隙氢原子促进了位错的移动能力从而促进相变，进一步导致峰值应力的降低.此外，氢原子的引入使双晶α-铁在未施加任何载荷时就已经产生晶格畸变.氢原子含量越高，晶界结构偏差越明显，位错成核越容易形成[25]，这也是峰值应力随氢原子浓度增加而降低的原因之一.

图7 (a)无氢36.86°模型在曲线骤降时的原子结构图；(b)氢浓度为2.2%的36.86°模型在曲线骤降时的原子结构图Figure 7 Atomic structures of the 36.86° model with (a) free hydrogen (b) a hydrogen concentration of 2.2% at the dip of the curve

峰值点之后，模型进入塑性阶段，为了解释氢原子在塑性阶段对ATGB双晶α-铁相变发生的影响，图7给出了无氢36.86°模型以及氢浓度为2.2%的36.86°模型在曲线骤降时的原子结构图.可以看出，双晶α-铁的塑性变形行为与氢原子无关，在所研究的加氢模型中，塑性变形同样主要通过从BCC到FCC再到BCC的相变来实现.同时，从应力应变曲线可以看出，峰值点对应的应变值随着氢浓度的增加而降低.这是由于氢原子存在于BCC晶格的八面体间隙位置，在应力加载前就导致了部分铁原子发生晶格畸变，同时也减弱了铁原子之间的结合力，因此在拉伸载荷的作用下使得BCC相向FCC相的转变更容易发生.此外，与加氢初始模型相比(图1(b))，在拉伸过程中，氢原子明显倾向于向晶界和自由表面移动.

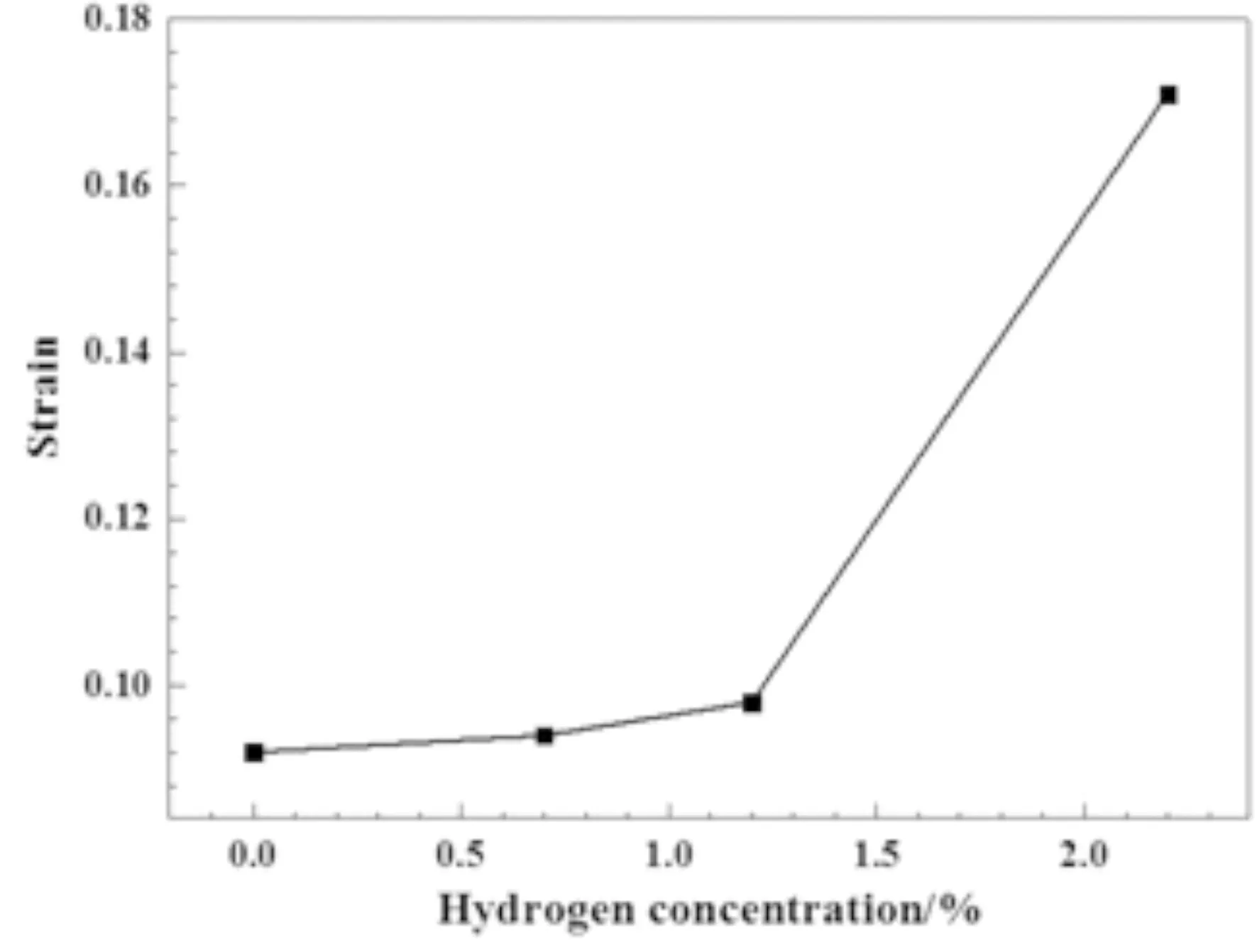
图8 氢浓度与FCC相向BCC相开始转变时应变值的关系曲线Fig. 8 The relationship between the hydrogen concentration and the strain value of the FCC phase to the BCC phase

上文提到在无氢模型中，随着应力的进一步加载，在塑性变形后期，出现了FCC相向BCC相的转变.同样地，在加氢模型中也出现了上述现象.为了进一步研究氢原子对相变发生的影响，图8给出了氢浓度与FCC相向BCC相开始转变时应变值的关系图.可以看出，随着氢浓度的增加，相变起始点推迟.这是由于分布在FCC相中的氢原子阻碍了FCC原子的退化.从图5(a)中的点阵变化关系可以看出，原本位于BCC相的八面体中心位置的氢原子在转变为亚稳态FCC相之后仍然处于八面体中心位置，而从图5(b)可以看出，FCC相中的八面体中心位置恰好是BCC晶格中棱的位置，所以FCC相到BCC相的转变必须有氢原子的移位.从图7(b)原子结构图也可以发现，FCC-BCC相变过程中，熔有氢原子的FCC相在转变成BCC相以后，氢原子转移到了界面处，BCC相中没有氢原子的存在.这也就是氢原子阻碍FCC相向BCC相转变的原因.

4 结 论

采用分子动力学模拟方法研究了温度为300 K时双晶α-铁在拉伸载荷下晶界旋转角和氢原子浓度对其变形机制的影响.研究结果表明，双晶α-铁的塑性变形主要通过BCC相向FCC相，再向BCC相的转变进行，且该变形机制不依赖于氢原子的浓度.由于晶界两侧Schmid因子不同，塑性阶段相变区呈现不对称特征.随着氢浓度的增加，间隙氢原子减弱了铁原子之间的结合力从而导致双晶α-铁的峰值应力减小.位于BCC晶格八面体间隙的氢原子的加入降低了铁原子之间的结合力，从而使得BCC相向FCC相的转变更容易发生.亚稳态FCC相中的氢原子位于新BCC晶格棱的位置，由此也有效阻碍了FCC相向BCC相的转变.