双光子J-C模型实现非定域双原子系统量子特性的远程控制

郭耀武, 高德恒, 韩 锴, 李英德, 赵加强

(潍坊学院物理与光电工程学院，潍坊 261061)

1 引 言

光与原子的相互作用系统的非经典特性是近代量子光学研究的重要内容之一. 以J-C模型为基础对光与原子的相互作用的量子特性已进行了大量的研究,如原子布居差的崩塌-回复效应和偶极压缩效应,并作了多种形式的推广[1-3]. 早期的研究大都局限于初态原子处于非纠缠态的假设；而对于初态为纠缠态的原子,近年来也取得了一些研究进展, Yang等人[4]提出初始处于纠缠态的两个二能级原子，其中之一与腔场发生相互作用，通过控制腔外原子来控制腔内原子的发射性质. Xiang[5]等人用相同的方法来控制腔内原子的偶极压缩. 这些研究都利用了纠缠的奇妙关联来远程控制原子的非经典特性.

近年来,作为上述控制基础的量子纠缠也受到人们的重视, 它对于Bell基的制备、量子隐形传态[6]、量子密集编码[7]和量子计算[8]等有重要的理论和实验意义，其中纠缠态的制备和操作是核心. 利用选择性测量来操纵纠缠态是近年来出现的一种方法,对一个纠缠系统的子系统进行测量不仅能给出子系统的信息,而且还提供了对其它子系统进行操纵的可能性. Ye[9]研究了在非线性J-C模型中，处于最大纠缠状态的两原子之一与相干态光场发生相互作用，通过选择性测量实现了未和场有相互作用的原子与场的纠缠，并研究了测量对光场非经典性质的影响；相比于单光子相互作用系统，双光子共振相互作用过程中原子表现出更强的非经典特性，其中张国锋等[10]在双光子J-C模型中研究了两纠缠原子的纠缠度对测量后光场非经典性质的影响，同时也实现了原子和场的纠缠. 以上研究主要是用对原子进行测量的方法进行的,而未考虑相干光场参数值和光子探测的影响.

本文中我们考虑了空间分离的两纠缠原子之一与单模腔场发生双光子共振相互作用,经腔QED演化后,对单模腔场进行光子探测和选择两原子不同的初态纠缠度,通过操纵演化时间t和探测到的光子数n以及光场参数α来远程调控腔外A原子的偶极压缩,同时用相同方法实现了对远程控制的信道-腔外原子A和腔内原子B之间的纠缠的控制，并且证明纠缠和压缩存在一定的对应关系.

2 理论模型及其波函数

设初始时刻,A,B两原子系统处于如下纠缠态:

(1)

图1 系统的框图.Fig. 1 System diagram

在旋波近似下,单模双光子J-C模型在相互作用绘景中的哈密顿量表示为(ħ=1)：

HI=λ(a2σ++a+2σ-),

(2)

其中,σ±是原子的算符,a+,a是腔场的产生算符和湮灭算符,λ是相互作用耦合常数. 设最初腔场处于相干态|α〉,系统的总态矢为:

(3)

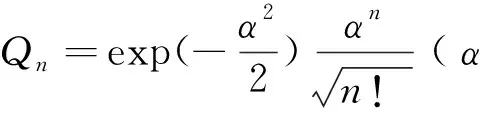
(4)

(5.1)

(5.2)

(5.3)

(5.4)

对腔场进行光子探测,假设探测到的光子是|n〉态,系统的波函数变为:

(6)

其中N为归一化常数.

3 原子A的偶极压缩效应

对于一个有赝自旋算符S±,S3描述的二能级原子，定义两个厄米算符[11]：

(7)

S1,S2满足下列对易关系：

[S1,S2]=iS3

(8)

相应的不确定关系为：

(ΔS1)2(ΔS2)2≥〈S3〉2/4

(9)

这里(ΔSi)2=〈Si2〉-〈Si〉2(i=1或2)是原子算符Si的量子涨落.如果存在某个态|Ψ〉，使得Si的量子涨落满足

Fi=(ΔSi)2-2-1|〈S3〉|<0

(10)

原子就呈现偶极矩压缩效应.

由(4)和(10)式很容易得出,未对腔场进行光子探测时,原子A没有压缩效应,对于进行光子探测后的波函数(6)式,代入(10)式可得F1没有压缩,我们通过数值计算给出F2随时间的演化及随α,n的变化关系,如图2.

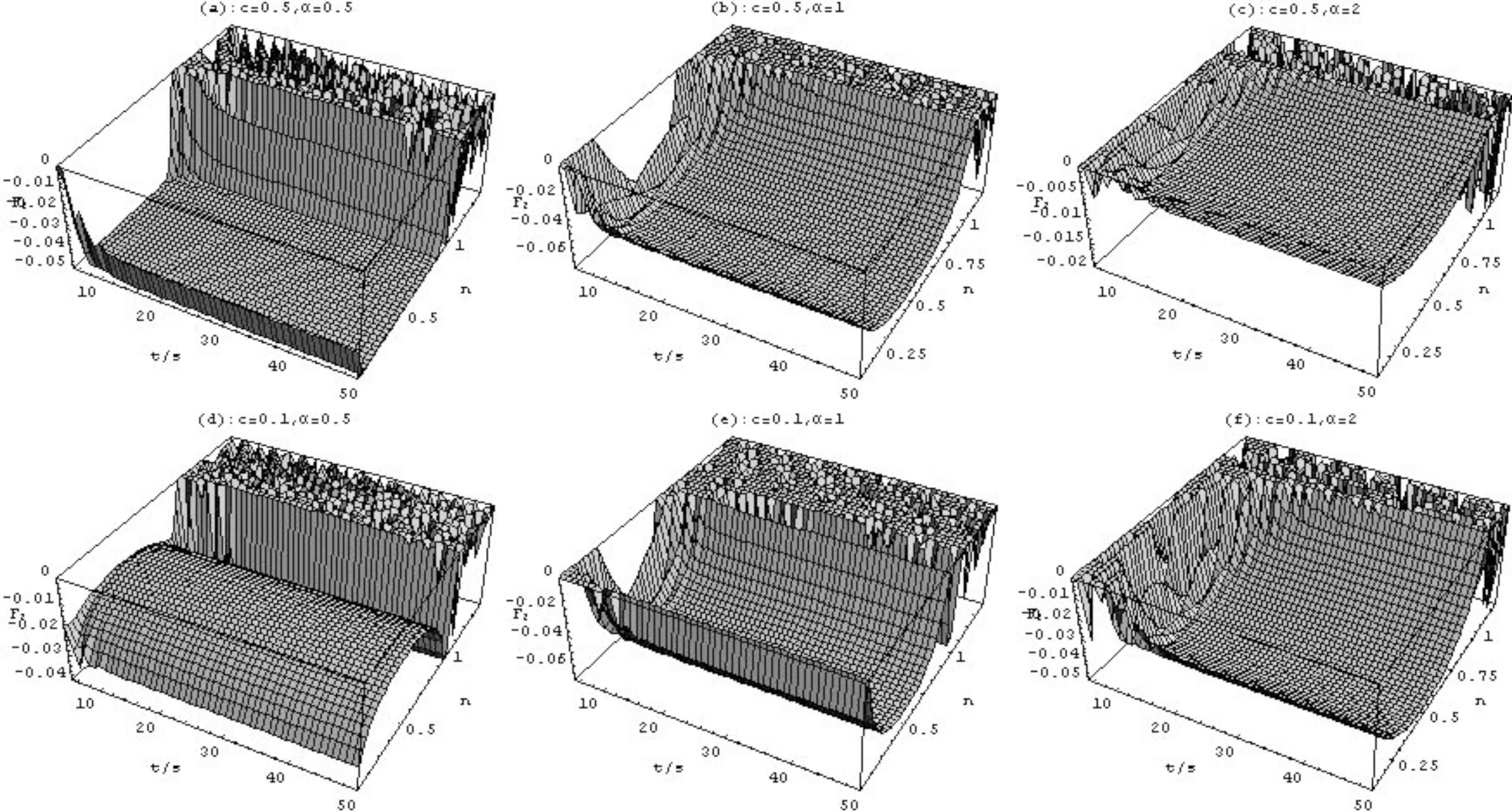
图2 在不同光子数下，F2随时间t的演化Fig. 2 Time evolution of F2 for different photon numbers

(1)首先我们取A,B两原子的初态处于最大纠缠(c=0.5)的情况, 当α的值非常小时,经计算可知压缩不明显；当α=0.5时,如图2-(a),探测的光子数n在小于1的范围内,原子A对应的F2从特定的时间点开始,随时间的演化出现比单光子过程更加明显的压缩效应,而且压缩随时间的变化始终存在. 当光子数n在大于1的范围内,压缩随时间t和光子数n的变化密集分布，且压缩值较小. 当α的值取1时,如图2-(b),在光子数小于1的区域,F2仍然随时间t的演化一直存在压缩,但最大压缩值变小,并且在n轴的方向上压缩值不相等的,而是呈现下凹的弧状；在n大于1的区域，与图1相比，压缩出现的频率明显降低，并且随光子数n的增大，压缩分布基本不变；当α增大到2时，如图2-(c),在n小于1的范围,压缩随时间的演化不发生变化,与图(a),(b)相比较,压缩值变得更小,在n大于1的范围内与图(b)相比, 压缩出现的频率增大,又重新回到分布密集的情况. 用以上相同的研究方法,我们得知当α的值继续增大时,压缩效应逐渐不明显,直至消失.

(2)当初态原子A,B不处于最大纠缠的情况下,我们选取c=0.1,如图2-(d),(e),(f)所示,对于n大于1的区域,压缩分布规律与初态为最大纠缠的情况(图2-(a),(b),(c))相似；对于n小于1的区域，当α=0.5时，如图2-(d)，一直存在压缩，且随时间的演化规律不发生变化，压缩值分布在n轴方向上呈现上凸的弧状. 当α=1时，如图2-(e)，与图(d)相比,最大压缩值变大,且压缩值在n轴上的分布变为下凹的弧状. 当α=2时,如图2-(f),最大压缩值又变小. 总之，我们可以通过选取不同的初态纠缠度与合适的时间t,操纵相干光场的参数α和探测到的光子数n,就可以实现远程调控原子A的偶极压缩效应.同时我们也可以看到选择此模型能够很好地控制由于原子的行为而造成的量子噪声.

4 原子A、B之间的纠缠演化特性

对于两个子系统构成的复合系统的混合态，我们用Peres提出的用部分转置矩阵的负本征值判断纠缠的方法来度量纠缠度，即对于密度矩阵ρ表示的两子系统中，纠缠可以用部分转置矩阵的负本征值[12]来定义，

(11)

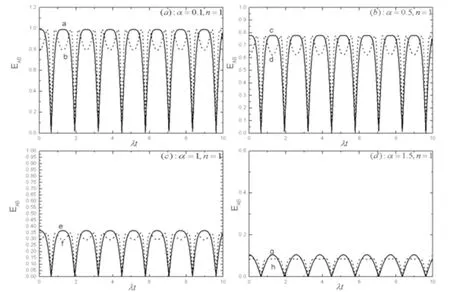
式中的μi-是部分转置矩阵ρ的负本征值. 当EAB=0，两子系统是分离的[13]，当EAB=1时两子系统处于最大纠缠；当0

图3 EAB随时间的演化Fig. 3 Time evolution of EAB

(1)当探测到光场处于真空态时，即n=0，如图3所示,在图3-(a)中α=0.1,两原子的纠缠出现周期性的演化,在一个周期内，纠缠度先增大,增大到最大纠缠状态, 这相当于原子和场不发生相互作用,双原子系统处于原来的状态, 保持一段时间然后又减小,直到完全分离(曲线a),对于初态为非最大纠缠态(曲线b),在一个周期内，纠缠度先增大,达到最大纠缠后减小,减小到某一确定值后又增大,达到最大纠缠,然后再减小直到完全分离. 比较曲线a和b,可知初态纠缠度改变了纠缠随时间的演化特性,影响处于最大纠缠的持续时间，但两者具有相同的纠缠演化周期.

随着光场参数α值的增大,如图3-(b),(c),(d)所示,对于初态为最大纠缠和非最大纠缠两种情况(曲线c,d,e,f,g,h),纠缠演化特性不变,周期相同,但纠缠度的最大值随α值的增大而减小. 当α大于1.5时,纠缠几乎消失，接近退纠缠状态.

(2)当探测到的光子数为1时,如图4所示，对于图3和图4对应的部分进行比较发现：当原子初态为最大纠缠和非最大纠缠两种情况下，我们可以看到纠缠也出现周期性的演化,但是由于腔中光子数的存在使演化的周期变短，这是由于光子数影响(6)式中系数的函数周期所致. 纠缠度的最大值随α增大而减小(图4-曲线a，b，c，d，e，f，g，h),与图3有相同的演化特性. 当我们用相同的方法研究光子数n大于1的情况时，发现纠缠随光子数的增加变的越来越不明显，纠缠度越来越小，退纠缠现象明显. 总之，通过改变原子的初态纠缠度和光场参数α，及其探测到的光子数n，能够很好控制纠缠演化的特性.

对本文第3和第4部分的分析结果进行比较，在光子数n大体小于1的情况下，压缩效应明显，而且随时间的演化一直存在，同时对应着原子间纠缠的周期性演化也非常明显，并且可以出现最大纠缠态；在光子数大于1的情况下，压缩和纠缠效应都迅速变的不明显，随着压缩的消失，纠缠也逐渐消失. 由此可知腔外原子A的压缩和原子A,B间的纠缠存在一定的对应关系.

图4 EAB随时间的演化Fig. 4 Time evolution of EAB

5 结 论

本文利用旋波近似下的双光子J-C模型，让一对纠缠原子之一与单模腔场发生双光子共振相互作用，求出系统的波函数，然后对演化后的腔场进行光子探测，计算了腔外原子A的偶极压缩，通过对相互作用时间t，光场参数α以及探测光子数n实行一定的调控，对未参与相互作用的原子A来说，我们可以在更大程度上远程调控其偶极压缩效应；同时，我们用相同的方法研究了对远程控制的信道-腔外原子A和腔内原子B之间的纠缠进行控制，并且得出原子压缩与原子系统的纠缠存在一定的对应关系. 总之，本文的研究对于量子远程控制、量子通讯具有一定的指导意义.