多面体系统定结构H2/H∞控制器优化设计
2019-04-28郭雅丽
王 飚,郭雅丽
(长安大学电子与控制工程学院,陕西 西安 710064)
0 引言
由于环境的复杂性,构建的模型一般为非线性系统,通常需要将非线性模型转化为线性模型再进行研究。但是这种方法精确度低下,难以满足人们的需求。鲁棒控制应运而生,并且在多个领域应用广泛。H2设计可使系统性能更优良,H∞设计对系统的不确定性有更好的鲁棒性,混合H2/H∞能够很好地将优良的性能与鲁棒性结合起来。但是该方法存在设计过程较复杂、阶数高的缺点,很难在工业现场得到广泛应用[1]。近年来,低阶、定阶以及定结构系统以其成本低、易实现等优点,重新受到了人们的重视。固定结构控制器设计在理论和实践中都是一个具有挑战性的问题。其中,非凸秩约束和双线性矩阵不等式(bilinear matrix inequalities,BMI)在计算上难以实现。一些研究者尝试解决这些非凸和BMI问题,以找到一个局部最优控制器,因而提出了几种降阶的迭代方法来设计控制器[2-3]。多面体表示是描述物理系统参数缺乏的一般方法。这种不确定性包括区间参数不确定性[4]、椭球参数不确定性[5]以及多模型系统不确定性。对于多面体系统,固定结构控制器的设计更加复杂。本文结合极点配置,提出了一种基于线性矩阵不等式(linear matrix inequalities,LMI)的定结构H2/H∞[6]控制器设计方法。
1 鲁棒控制及LMI介绍
考虑以下状态空间方程描述的线性时变不确定系统[7]:
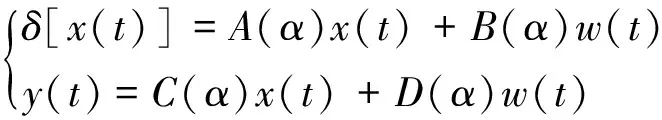
(1)
式中:x为状态变量;w为外源性输入;y为输出;δ[·]为连续时间系统的导数算子和离散时间系统的前向算子;(A,B,C,D)(α)为凸有界(多面体)不确定的域φ。
(2)
式中:任何不确定矩阵(A,B,C,D)(α),可根据参数变量α表示为多面体顶点(Ai,Bi,Ci,Di)的凸集合。
1.1 H2和H∞范数
1.1.1 H∞范数
标准H∞控制[8-10]结构如图1所示。
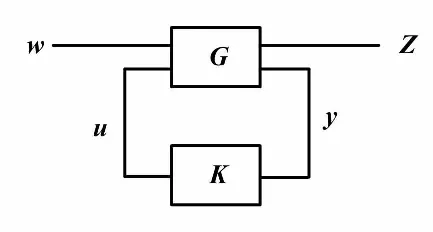
图1 标准H∞控制结构图
H∞控制的目的就是设计反馈控制器K,使得闭环系统稳定,并确保从扰动输人w到被控输出z之间的闭环传递函数Tzw的H∞范数极小或小于某一正实数γ,即:
‖Tzw(s)‖∞=Supσmax[Tzw(jw)]<γ
(3)
H∞范数是系统频率响应的最大奇异值的峰值,它反映的是系统保持稳定状态下所能承受的最大扰动度量,主要考虑系统的鲁棒稳定性,对系统的动态性能则没有要求。
1.1.2 H2范数
H2控制[11-12]的目的就是设计状态反馈控制器K使得闭环系统稳定,而且从扰动输人w到被控输出z之间的闭环传递函数Tzw的H2范数极小或小于某一正数γ,即:
(4)
系统的H2范数具有明确的物理意义,它的平方等于系统脉冲响应总的输出能量,也等于系统在白噪声输入时系统稳态输出方差。其既反映了系统的动态性能,又是控制系统的一个重要性能指标。
1.1.3 H2/H∞混合控制
在实际问题的处理中,对控制指标的要求是多方面的,既要求在有扰动的情况下系统能够保持稳定(即扰动到被控输出的闭环传递函数的H∞范数小于某一-γ0),又要求从扰动到被控输出的闭环传递函数的H2范数尽可能小,以提高系统的动态性能。H2/H∞混合标准控制系统如图2所示。
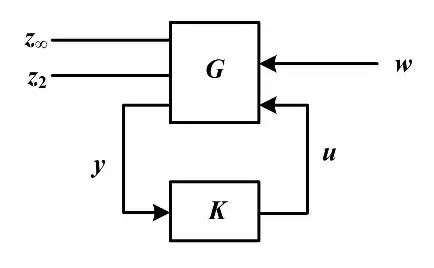
图2 H2/H∞混合标准控制系统框图
图2所示的H2/H∞混合标准控制系统中:w为外部输入(如参考信号,干扰噪声等),z∞与z2分别表示与H∞指标、H2指标相关的输出信号,u为控制输入信号,y为测量输出信号,G为广义被控信号,K为控制器。
H2/H∞混合控制问题是针对广义的被控对象来设计动态反馈控制器,必须满足以下设计标准。
①图2所示闭环系统内稳定。
②闭环传递函数阵Tz∞w(s)满足‖Tzw(s)‖∞<γ。
③闭环传递函数Tz2w(s)满足min‖Tzw(s)‖2。
这样的控制器K称为H2/H∞混合的最优控制器。
1.2 不确定性系统鲁棒控制器的设计
考虑下面离散线性时不变单输入单输出系统传递函数:
(5)
式中:参数变量θ为有着q个顶点的多面体;co{θ1,θ2,θ3,θ4)为一组凸包。
设计一个标准的负反馈结构控制系统,其核心是设计一个定结构控制器:
(6)
该定结构控制器需满足以下要求。
①闭环系统是内在稳定的。
②闭环系统实现了范数小于常数γ。
利用LMI对定结构鲁棒控制器性能进行评估,并且引入Schur稳定多项式来构建传递函数矩阵:
E(z)=enzn+en-1zn-1+…+e1z+e0
(7)
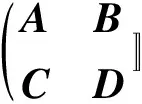
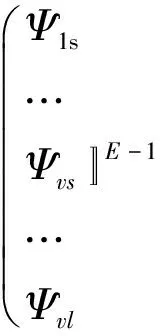
(8)
式中:Ψ为多项式,依赖于参数变量θ;A、B、C、D为常数矩阵。
1.3 关于线性矩阵不等式的结论
在鲁棒控制中,解决不确定问题常常转化为线性矩阵不等式系统的可行性问题,或带有线性矩阵不等式约束的凸优化问题。以下是定结构控制器的设计所需要的一些引理。
无论是林毅夫教授还是我们在课上探讨的结论,都可以看出我们并没有对理论盲目的尊崇,也没有认为理论是绝对正确的,而是将理论一分为二的看待,有时候理论与经验是相辅相成的,有时候理论与经验是背离的。从这点我们可以看出,经济学与教育学对于理论与经验问题的看法是一致的,教育学并不是孤立存在的,它与其他学科是有互通的。
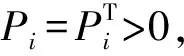
Con1(Hi,Pi,E)<0
(9)
Con1(Hi,Pi,E)>0
(10)
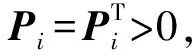
(11)
(12)
2 实例分析
2.1 标准系统的控制器的设计
以下系统有三个不稳定极点:
(13)
为此,系统设计一个定结构稳定控制器,并且这个控制器的加权闭环传递函数的范数要小于最小上限。
(14)
(15)
2.1.1 全阶控制器的设计
在解决定阶控制器的设计之前,要阐述一下本文提出方法的优点,那就是范数边界单调递减到一个定值。
(16)
设计了一个与K1(z)有着相同结构(5阶)的控制器。一般而言,选择的中心多项式要包含权函数的分母。选择中心多项式E(z)=Wd(z)(z-0.5)8,零点在z=0.5。
加权传递函数H(z)与中心多项式范数的更新如图3所示。

图3 加权传递函数H(z)与中心多项式范数的更新
图3表明,这个方法可快速收敛到相同的范数边界7.453 8。
现在考虑一个5阶控制器的设计:
(17)
式中:K2的范数为2.014 6,比K1小得多。
2.1.2 低阶控制器的设计
以上所设计的设计器K1(z)有两个不稳定的极点,所以传统的方法不能减少控制器的阶数,使其小于两阶。现在设计一个一阶控制器,使中心多项式5次迭代更新后得到下界γ=2.243 1:
(18)
为了显示中心多项式对结果的影响,考虑中心多项式E(z)=Wd(z)(z-a)4。a分别取0.1、0.2、0.3、0.4、0.5。不同中心多项式对范数的影响如图4所示。对于不同的多项式,有一阶控制器的加权闭环传递函数的范数边界的单调递减。
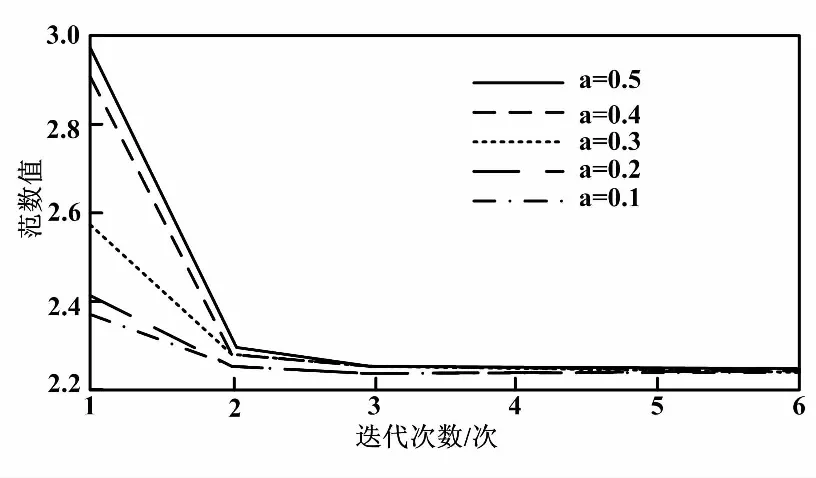
图4 不同中心多项式对范数的影响
2.2 多面体系统的控制器的设计
考虑一个被多面体不确定性影响的3阶系统:
(19)
式中:θ0=-0.2;θ1=-1.2;θ2=0;θ3=-0.1。
假设所有的参数相较标准系统不确定性达到±12%,所以参数的不确定性可以用一个16个点的多面体(超立方体)形式体现。
为此,系统设计一个二阶控制器,包括一个积分器和能得到最小范数边界γ的传递函数。
(20)
首先,对于所有的点,都考虑一个普遍的中心多项式E(z)=Wd(z)(z-0.5)5,并且使用引理1中的条件生成一个有着上界γ=1.297 32的二阶稳定控制器。
然后,使用引理2,解决下列的优化问题:LMI条件满足则存在最小的γ。这样就得到了一个鲁棒控制器。将其作为稳定控制器,然后经过一系列迭代后得到下列的控制器:
(21)
对于这个控制器,范数的上界γ=0.552 72。这样,经过一系列的迭代改善了鲁棒控制器的性能,使得范数上界单调递减。
2.3 试验结果分析
采用HIFOO评估所设计的控制器。HIFOO是为定阶控制系统设计的一个MATLAB工具包,用于设计不确定系统定阶控制器。使用程序语言定义变量并描述各个线性矩阵不等式,写出优化条件min‖Tzw(s)‖2,利用mincx函数求解线性矩阵不等式组,得出相应结果。
取γ=0.55272来验证1.1.3节中提出的系统的各项性能指标。此时,对应的H2范数为0.256 3,系统的闭环极点都在左半平面,所以闭环系统稳定,满足第一个条件。从‖H∞‖<γ可以看出,其仍然满足二个条件。当γ=0.552 72时,H2范数为0.256 3,显然小于H2范数的上界,满足第三个条件。
因此,本方法设计的控制器满足H2/H∞混合控制的各项指标。从系统的极点分布来看,系统有一个负实主导极点。它使得控制系统处于过阻尼状态,系统对扰动的响应速度相对缓慢,这也使得系统本身具有较好的鲁棒性。此例中,本文的控制器效果更好,而且更重要的是,它保证了整个多面体的性能不仅仅是点,即本文控制器适用于系统的所有状态,而非某一状态。
3 结束语
本文采用线性矩阵不等式方法,提出了多面体系统定结构控制器的优化设计方法。该方法基于定结构非凸集的内凸逼近,给出了鲁棒控制器的设计。试验结果表明,通过多次迭代结果会收敛于次优解,并且范数上界会出现单调递减。通过标准系统全阶低阶控制器和不确定系统定阶控制器的实例分析以及试验仿真,验证了此方法的可行性。该方法设计的鲁棒控制器增益小、动态性能好、鲁棒性强,满足混合控制器的性能指标。
