基于数据驱动的全工况下燃气轮机基准值确定
2019-04-28顾煜炯韩旭东朱俊杰黄元平
王 仲,顾煜炯,韩旭东,朱俊杰,黄元平
(1.华北电力大学能源动力与机械工程学院,北京 102206;2.广东粤电中山热电厂有限公司,广东 中山 528445)
0 引言
燃气轮机因其启停灵活、污染物排放水平低等优势,近年来在我国得到飞速发展,装机容量有了显著提升[1]。目前,为了保证燃气轮机运行的安全性,常参照制造厂商给出的等效运行小时数安排维修计划。这种维修方式没有考虑机组的实际运行状态,设备既有可能提早发生故障,也有可能在运行状态良好的情况下维修部件,增加了电厂的运维成本[2]。因此,燃气轮机运行调整与维修决策方案的制定依据机组的实际运行状态,其中的关键在于机组基准值的确定。
传统的基准值确定方法一般有两种:一种是以设计值作为基准值,另一种是以最近一次的性能试验值作为基准值。这两种方法普遍存在的问题是燃气轮机在设计与性能试验时的工况与实际工况存在一定的偏差[3]。随着信息技术、数据库技术和先进测量技术的飞速发展,工业过程积累了海量的运行数据。近年来,国内外不少学者尝试用数据驱动方法进行发电机组能耗分析与运行优化研究。赵欢等利用模糊C均值聚类方法确定典型负荷邻域区间内火电机组特征参数的基准值[4]。Andrew Kusiak等利用聚类算法解决了火电机组历史运行状态模式分类问题,建立了不同工况下参数之间的关系[5]。其直接从历史数据中获取信息,避免了复杂数学模型的建立,并且能够全面、真实地反映机组的实际运行水平。然而,由于燃气轮机参与调峰运行,所以其工况复杂多变,运行数据的模式多样。现有的文献在进行数据挖掘前,没有考虑燃气轮机数据的特点。
针对燃气轮机多工况下基准值确定的问题,本文提出了一套基于数据驱动确定全工况下燃气轮机基准值模型的方法。首先,对历史数据样本进行稳态筛选;其次,根据边界条件对燃气轮机进行工况划分,确定典型工况下参数的基准值;最后,选用某实际燃气轮机的实际运行数据,验证模型的有效性。
1 燃气轮机基准值模型的提出
燃气轮机的历史运行数据反映了真实的运行状态。燃气轮机在实际运行过程中工况多样,涉及稳定状态与非稳定状态、不同边界条件下的运行状态以及自身健康状态的好坏差异等。因此,在通过历史数据挖掘燃气轮机基准值之前,需要对数据进行有序的梳理。首先,以功率为特征变量,利用区间估计的方法,筛选历史运行数据中的稳态工况;然后,以功率、环境变量为特征边界条件,利用K-均值聚类算法,划分稳态工况;最后,在此基础上,对每个工况下变量的样本建立多元高斯混合模型,以热耗率最低为目标选择该工况下的基准值。
基于数据驱动的燃气轮机基准值模型如图1所示。
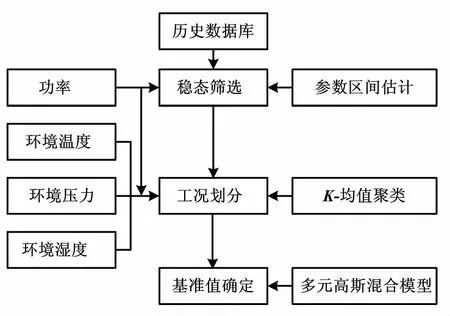
图1 基于数据驱动的燃气轮机基准值模型
1.1 稳态筛选
为了满足电网负荷调度的需求,燃气轮机快速地调整燃料供给与其他运行参数。在此过程中,产生了非稳态工况。燃气轮机参数的测量值可以视为真实值和噪声值的叠加。当燃气轮机处于稳态工况下,参数的真实值保持不变。测量值的变化主要是由随机误差引起的。当燃气轮机处于非稳态工况下,参数的真实值发生急剧变化,甚至在短时间内产生很大偏移量。机组的非稳态工况直观地反映在输出功率的变化上,输出功率随时间呈单调递增或递减的特点[6]。因此,选用输出功率作为稳态判别的特征变量,其表达式为:
(1)
式中:pt为t时刻功率的测量值;μ为功率的真实值;m为功率的变化速率;ε为功率的随机误差,服从正态分布。
由式(1)可以看出,稳态与非稳态工况的区别在于功率变化速率是否等于0。为了便于对m值大小进行估计,计算相邻两个时刻功率的差值Δp,如式(2)所示。
Δp=pt-pt-1=m+(εt-εt-1)
(2)
因为随机误差ε服从正态分布,因此统计量Δp的期望等于m。根据时间序列的性质,m可以用时间窗口内样本统计量的均值估计,如式(3)所示。
(3)
式中:h为采样时间窗口内的样本数目。
为了保证估计的可靠性,采用区间估计的方法,确定样本功率差值的期望值m。如果估计的区间范围包括0,则认为机组有很大可能在该时间段内处于稳态工况;否则,认为机组处于非稳态工况。
1.2 工况划分
燃气轮机运行参数变化的原因可以归结为两类:一是运维可控类,包括运行调整不当、可维护类故障以及传感器故障;二是不可控制类,包括边界条件变化等。在确定参数基准值之前,需要对历史数据进行工况划分,隔离边界条件变化对参数的干扰。对于发电用燃气轮机而言,机组的输出功率由电网控制。因此,选用大气温度、大气压力、大气湿度、燃机功率4个变量作为边界条件,对稳态筛选后的历史数据进行工况划分。
聚类算法本身不需要建立复杂的函数模型,依据相似性对数据分类。作为聚类算法的典型代表,K-均值算法具有高效、快速的特点,被广泛应用于大规模数据进行聚类[7]。K-均值算法的基本原理是:首先,从数据样本中随机选取K个点作为初始的聚类中心;其次,计算并比较其他数据点到K个聚类中心点的距离,并对距离大小进行排序,将样本点划分到距离最近的聚类中心所在簇;待所有点分类结束后,重新计算每簇样本数据的平均值,将其作为新的聚类中心。不断重复上述过程,直至准则函数收敛,如式(4)所示。
(4)
式中:E为所有样本点的平方误差的总和;xj为第i类的第j个样本点;mi为第i个聚类子集的聚类中心。
K-均值聚类算法的聚类效果依赖于聚类数的选择。聚类数目过少,样本的特征不能够全面表征;聚类数目过多,又会将异常噪声数据当作正常类别进行处理,从而导致误分类。因此,采用silhouette准则确定K-均值聚类算法的最佳聚类数,将样本点silhouette准则系数平均值最大时所对应的K值作为最佳聚类数[8]。
1.3 基准值的确定
多元高斯混合模型(multivariate Gaussian mixture model,MGMM)是一种半参数的概率密度估计方法。它融合了参数估计法与非参数估计法的优点,不局限于特定的概率密度函数形式[9]。
如果模型中子模型足够多,则其能够以任意精度逼近任意的连续分布。MGMM的概率分布形式如式(5)所示。
(5)
(6)
式中:X为参数变量;q为子模型个数;ωq为第q个子模型模型的权重系数;φq(X|θq)为第q个子模型的概率密度函数。
MGMM的参数估计采用经典的最大期望值(expectation maximum,EM)算法。EM算法是一种迭代算法,适用于含有隐含变量概率模型的参数估计[10]。
MGMM的子模型个数会影响模型的回归效果,故选用赤池信息评价准则(Akaike information criterion,AIC),确定最佳子模型个数[11]。AIC建立在熵的概念上,提供了一种权衡模型复杂度与拟合数据优良的评价办法,其定义如式(7)所示。
AIC=2q-2ln(L)
(7)
式中:q为子模型个数;ln(L)为模型的对数似然函数。
2q作为惩罚模型复杂度的引入,有助于降低模型过拟合的风险。随着子模型个数的增加,AIC的值会先减小再增大。综合考虑模型的回归精度与复杂度,选择AIC最小时对应的子模型个数作为最佳子模型个数。
2 算例验证
选用某实际发电用燃气轮机进行基准值模型的验证。从电厂的厂级实时监控信息系统(supervisory information system,SIS)中采集燃气轮机10天的历史运行数据,测点变量如表1所示。设置采样间隔为1 min,共计14 400组样本点。
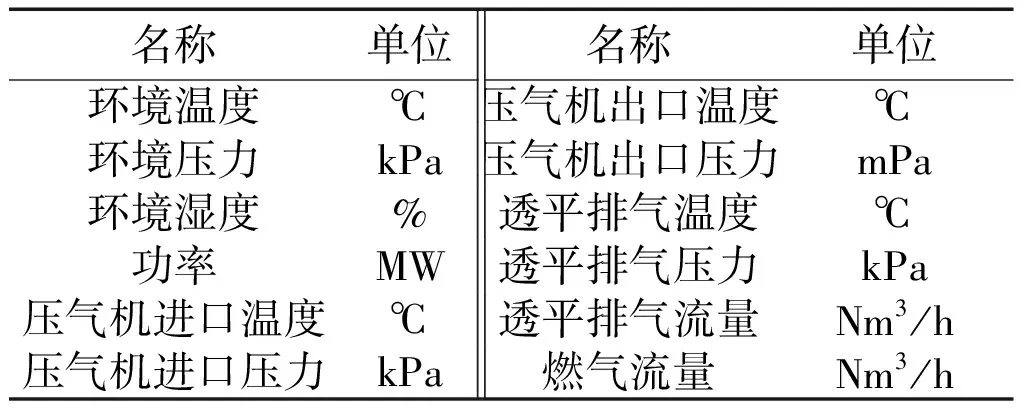
表1 SIS中采集的测点变量
2.1 历史数据的稳态筛选
首先,利用功率变化速率m区间估计的方法,对14 400组历史数据进行稳态筛选。其中,设置采样时间窗口长度h=20,区间估计的显著性水平α取0.05。稳态筛选后,共有13 541组样本被划分成稳态。稳态筛选前后燃机功率对比如图2所示。
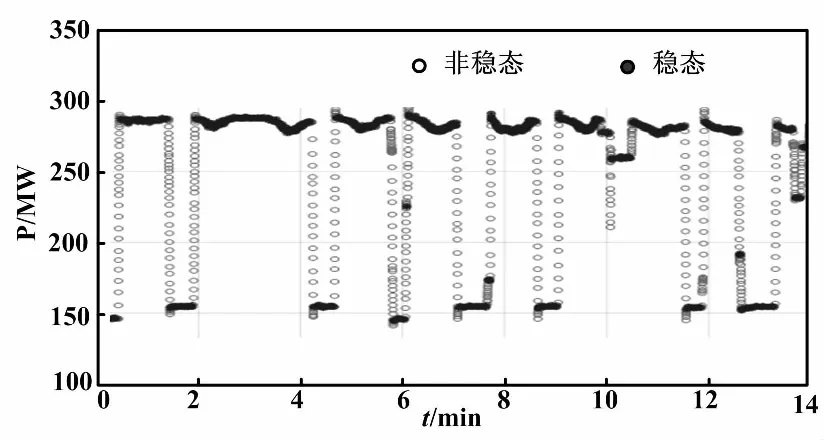
图2 稳态筛选前后燃机功率对比图
2.2 稳态工况的划分
针对稳态工况样本,利用K-均值聚类算法划分工况。为了确定最佳聚类数,依次计算不同聚类数目(2~30)下样本silhouette的平均值。当聚类数目是24时,silhouette值最大,等于0.62。因此,划分后24类工况对应的边界条件如表2所示。
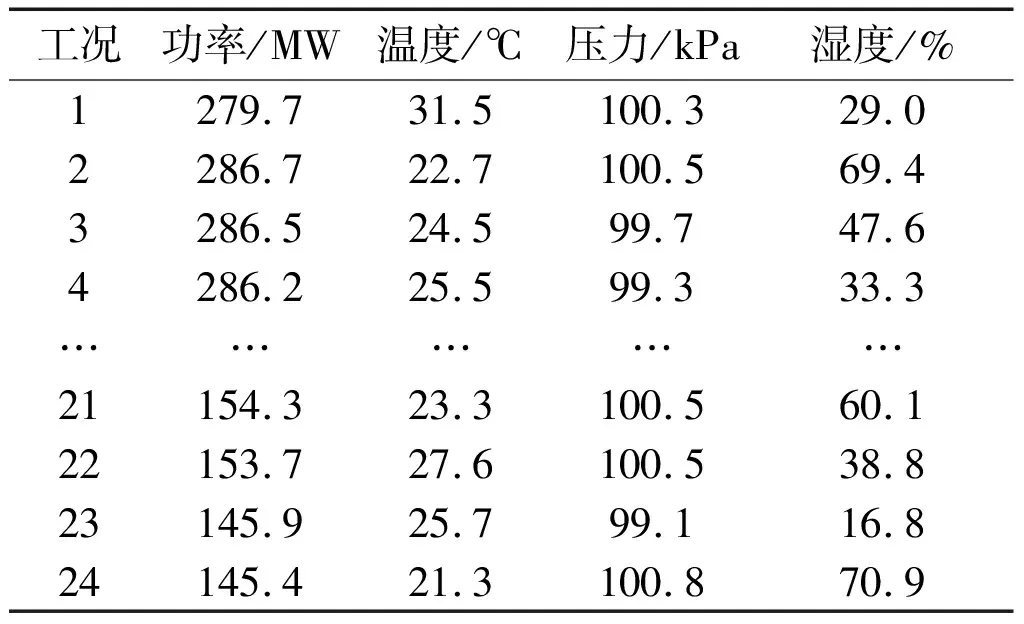
表2 24类工况边界条件
2.3 典型工况基准值的确定
利用MGMM确定每个工况下的参数基准值。以表2中第1类工况条件为例(即功率为279.7 MW,环境温度为31.5 ℃,环境压力为100.3 kPa,环境湿度为29%)进行具体说明。计算2~30个不同子模型数目下MGMM的AIC值,如图3所示。当MGMM子模型数目是8时,对应的AIC最小,用五角星表示。综合考虑MGMM复杂度和拟合精度,第1类工况条件下MGMM的子模型个数为8。

图3 不同MGMM子模型个数的AIC值
第1类工况条件下的MGMM拟合结果,即 MGMM回归的概率密度如图4所示。图4中,以压气机出口压力和透平排气温度作为特征变量,纵坐标为参数对应的概率密度。其中,坐标轴数值是归一化之后的值。比较不同子模型的期望,选择热耗率最低时对应的子模型参数期望值作为基准值,即9 554.57 kJ/kWh。同理,依次确定其他23类工况下参数的基准值。

图4 MGMM回归的概率密度
24类工况条件下热耗率的基准值如表3所示。
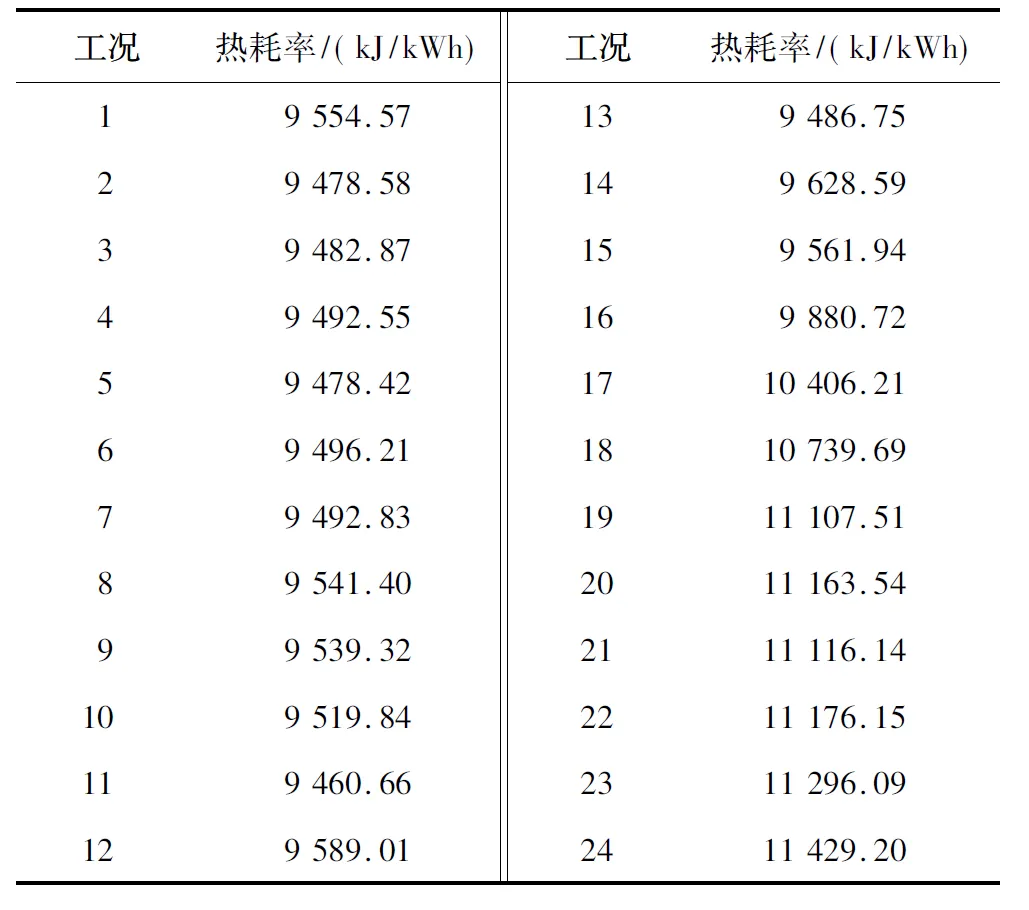
表3 24类工况条件下热耗率的基准值
3 结束语
本文提出了一种基于数据驱动确定燃气轮机基准值的模型方法。通过对历史运行数据进行分析、建模,建立全工况下参数的基准值模型。该研究方法的优势主要有以下几点。
①对燃气轮机的历史运行数据进行信息挖掘,使得参数的基准值符合机组的实际运行水平,有利于指导机组运行优化和故障诊断。
②在模型建立前,对历史数据进行稳态筛选和工况划分,有效排除了燃气轮机在非稳态工况以及边界条件的影响。
③在基准值求解过程中,考虑了随机误差以及参数之间的耦合特性的影响,建立多元高斯混合模型,以热耗率最低对应的子模型期望为基准值,保证了基准值的可达性。
在今后的工作中,将进一步研究燃气轮机基准值的动态模型,并积极拓展基准值在优化调整以及故障诊断中的应用。
