利用“特征函数”命制与求解数列问题

浙江省宁波市镇海区骆驼中学 (315202)

丁林蓬

1.初步感受利用特征函数在问题解决中的应用

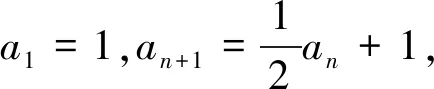
两个问题中的第一个问题都是对于数学归纳法的考察，对(1)(ⅰ)1≤a1<2可设1≤an<2，易得1≤an+1<2；(2)(ⅰ)过程类似.

第二问解法比较多，具体如下(以(1)的第二小题为例).

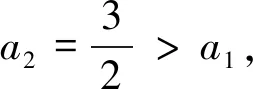
图1

设计意图：这两个问题的递推关系中，数列相邻项之间的关系相同.由于首项不相同，造成了数列在“有界性”和“单调性”上的大相径庭.这一特征可以呈现如下：

从特征函数的图像中不难看出，(1)与(2)两个问题的差异，由于两个数列的首项不同，导致了数学的单调性发生了改变.我们可以借助特征函数，快速观察数列的“上界”与“下界”，从而辅助“作差法”证明单调性的过程.基于此，给出变式如下，

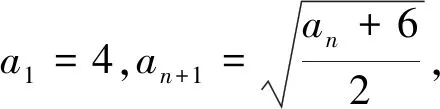
设计意图：这一问题是在例1的基础上，进一步观察特征函数的特点.与例1(1)相比较，数列首相相同，相邻两项之间的关系不同，导致了数列“有界性”与“单调性”之间的差异.

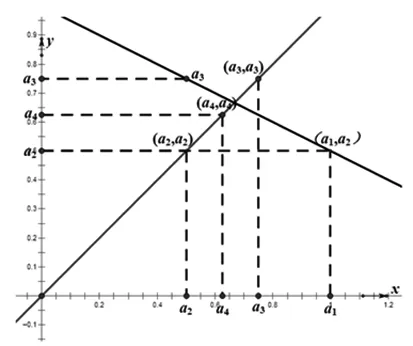
图2

从图2容易看出，数列的奇数项与偶数项分别具有自身的单调性与上、下界.其证明的过程，可以类比例1.

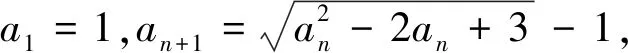
评析：以上从比较容易的一类递推公式入手，借助“特征函数”认识了数列的有界性与单调性，得到了证明单调性的一般方法——1:通过特征函数观察数列的上界与下界；2:数学归纳法证明数列的有界性；3:作差法求值域说明单调性.

2.从“点”、“线”、“面”的维度命制与解决问题

(1)猜想{a2n}的单调性，并给出证明；

图3

设计意图与解析：在初步形成了利用特征函数思考问题的习惯之后，我们可以从“数”与“形”两个角度认识图形，进而能够从平面的构成要素——点、线、面三个维度命制数学问题，呈现数学本质.

(2)是基于“线”这一维度命制的问题.

图4

这个定理，可以有效的佐证命题的科学性.关于问题的解决，可以采用这样的方法，

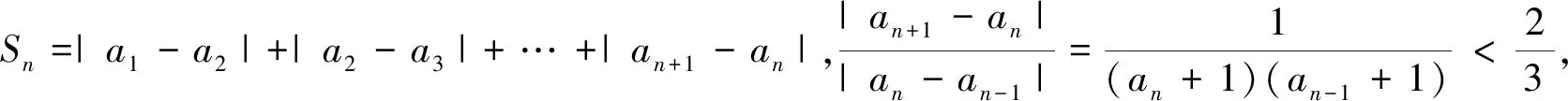
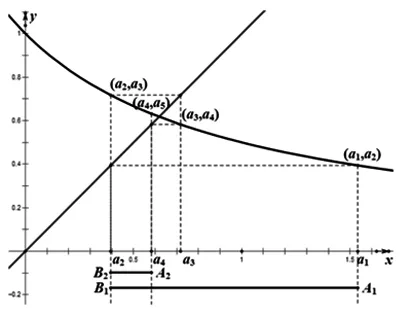
图5

图6

(3)是从“面”的维度命制的问题.如图6所示，该不等式的含义是曲线下边阴影部分(小矩形)面积之和小于曲边梯形a1MCD的面积，由简单的定积分知识可知，曲边梯形的面积为

(1)猜想{a2n}的单调性，并给出证明；

(1)证明{an}的单调性；

评析：以上立足与数列的特征函数，从“点”、“线”、“面”三个维度观察特征函数，命制一些具备思维量的数学问题.通过这样的过程，笔者越发感受到了，所谓的命题，就是通过巧妙地手段将数学本质“包装”起来.所谓解题，就是通过表象的数学条件，将隐藏的数学本质挖掘出来.

3.反思

正如，《作为教育任务的数学》中弗赖登塔尔所说，“学习数学唯一正确的方式是‘再创造’”.在经历了用函数的思想处理递推公式问题之后，笔者认为可以将函数思想进一步推广至研究数列的通项公式，而得到形如下：

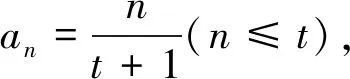
图7

评析：图7是借助函数思想分析这一问题的过程，本质上如同例3(4)相同，是曲线下小矩形面积之和小于曲多边形面积的问题，这里用到简单的定积分知识命制题目.

数学学科有自身区别于其他学科的核心素养，作为一线的数学教师，要立足教材，训练学生的“四基”；高于书本，提升学生的“四能”；注重对数学习题的挖掘，适度探究，从而帮助学生实现“三会”(会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界)，全面地提升学生的核心素养.