找准切入口 破解隐圆问题有方*
2019-04-28江苏省南京市第二十九中学高二210036
江苏省南京市第二十九中学高二(4)班 (210036)
刘乐舟 郭建华(指导教师)
在题设条件中没有直接给出圆方面的信息,而是隐藏在题设条件中,通过题意的深度理解和相关信息整合发现圆(或圆的方程),从而可以利用圆的相关知识求解,我们称这类问题为“隐圆”问题.下面就如何寻找解决“隐圆”问题的切入口做一些有益的探索.
类型一 圆的定义
到定点的距离等于定长的点的轨迹叫做圆.

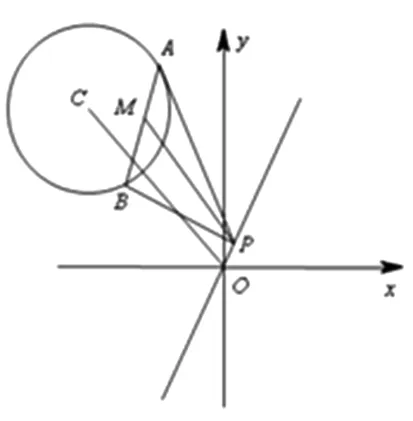

点评:求出线段AB的中点M的轨迹是解决本题的切入口,点M是“无”中生有的,为什么会想到求点M的轨迹呢?由圆C的弦AB为定长,显然弦AB的中点的轨迹为圆,自然就想到了构造圆,再转化为方程求解.
类型二 垂直关系圆
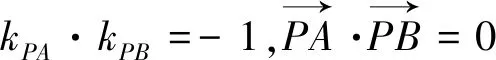
例2 在平面直角坐标系xOy中,直线l1:kx-y+2=0与直线l2:x+ky-2=0相交于点P,则当实数k变化时,点P到直线x-y-4=0的距离的最大值为_________.

点评:过定点的两条直线的垂直关系是解题的切入口,解题的关键是将垂直的位置关系转化为数量关系,进而求出点P的轨迹,使问题获解.
类型三 向量数量积圆
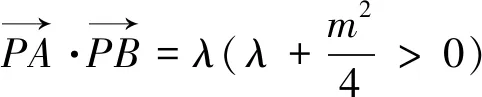
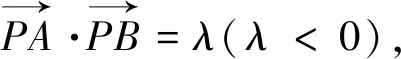
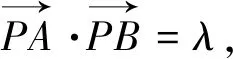
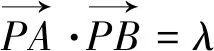
类型四 距离平方圆

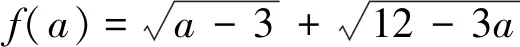

点评:分析无理式函数的结构是解题的切入口,再利用整体换元得到圆的方程,从而将代数问题转化为几何问题,结合直线与圆的位置关系进而使问题破解.
类型五 阿波罗尼斯圆

例5 在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在l上.若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
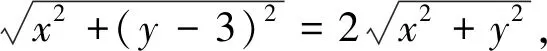
点评:将数量关系MA=2MO,通过“建系、设点、列式、代入、化简”等步骤得到“阿波罗尼斯圆”是解题的切入口,再结合两圆的位置关系进而使问题破解.
以上几个例子都是通过坐标系,充分挖掘题设条件将隐圆问题实现化“隐性”为“显性”,不愧为培养抽象核心素养的好素材,即在实现“化隐为显”的过程,找到解决问题最本源的知识和思想方法,从题中的具体背景中抽象出一般的规律和结构,并用数学的语言予以表达,从而深化对概念的理解、掌握、运用,运用数学抽象的思维方式思考并解决问题.
