一堂被学生“问倒”的研讨课的思考

浙江省杭州市富阳区新登中学 (311404)

杨志芳

笔者的《一类绝对值含参函数最值问题的探究》研讨课，从绝对值的含义、几何意义、三角不等式知识，利用了分类讨论、数形结合、参变分离、等价转换等思想方法，对这类绝对值含参问题进行探究,讲得头头是道，方法多样，巧思妙解，然而面对学生的质疑，解释苍白无力，令人遗憾，带给自己更多的思考，我们的习题教学应更关注什么？是否更贴近学生的思维水平.下面问题就是研讨课的一个例题.

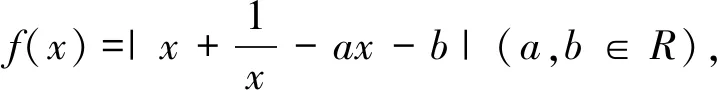
1.解法

笔者上课时给出了以下三种解法(略解如下)

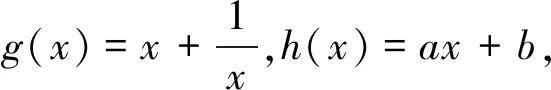
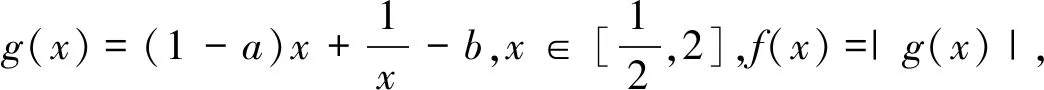
(2)当a<1时,b控制图像上下移动,所以不管a取什么值,必须g(x)max=-g(x)min时，f(x)的最大值取到最小，且M(a,b)min=

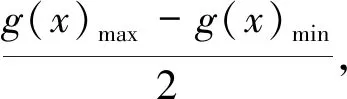
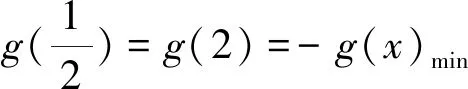
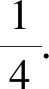
解法三:根据最大值的定义和三角不等式给出第三种解法如下.

一节课下来,教学任务“圆满”完成，学生也听得很认真，听课教师反映也很好，知识点“落实”思想方法的“渗透”感觉都比较到位，自己感觉比较“满意”.

2.质疑

学生惊叹老师的解法，有的同学提出自己的想法，老师您讲的方法很“巧妙”，特别是解法三，我是想不到的.我有几个疑问：

①为什么在去绝对值时有的要变号有的不变号？有的要乘以2，有的乘以3再相加？

面对学生质疑，当时只注重几种“妙法”，备课时没有预设到学生的问题.为什么只取这三点，当时仅对是否能得到一个常数，等号是否取到给予解释，“搪塞”过去，这个学生(可能代表一批学生)不是很“满意”接受.显然我们讲的“巧思妙解”与学生“一般”的思路有较大的落差，显然没有达到预期的教学效果.事后我也把这个“问题”在高三的一次集体备课中提出来，老师们也基本跟我的想法差不多，没有更好的道理使我信服.这个问题一直困扰着我，同时督促着我，要把它弄清楚，给同学一个满意的解释.

3.解惑

学生的问题是教学最好的资源，是教师最好的研究课题.疑问不解决，学生对问题的理解不透彻，不能把握问题的本质，也就失去了教学的价值与意义.

问题②诠释：为什么取这三个点，老师是怎样想到这三个点？要解决这个问题，我们需要换一种思路想想，即a,b能否用函数值来表示？两个参数是可以用两个函数值来表示.

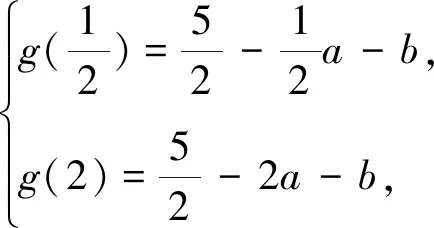
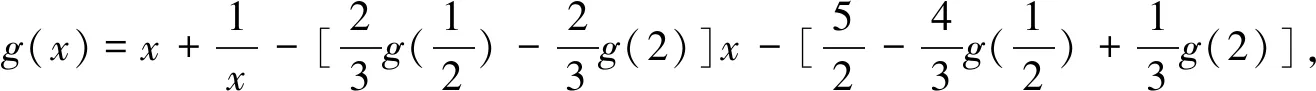
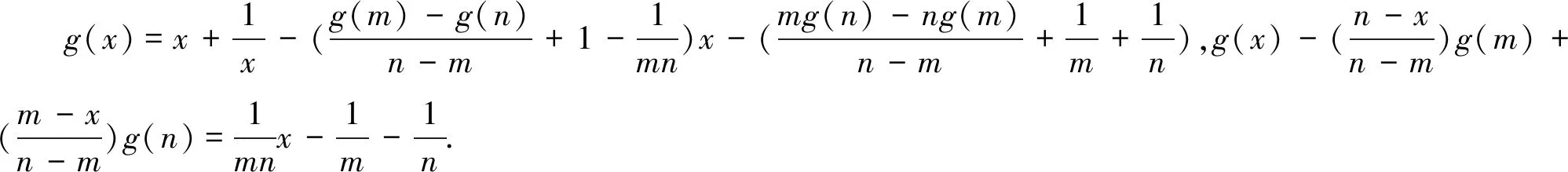
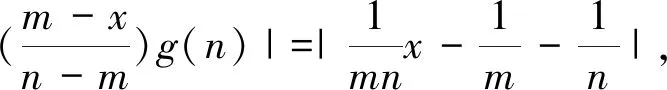
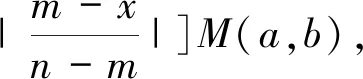
4.反思

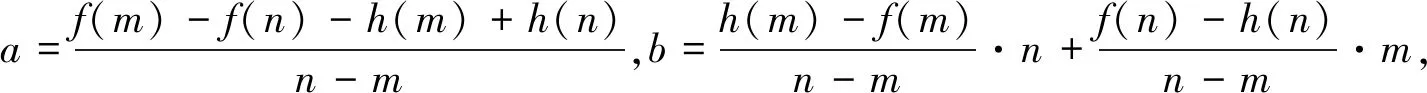
5.结语

解题教学是课堂教学的重要组成部分，我们在展示“巧思妙解”的同时，更要关注常规方法，要化神奇为一般，更要贴近学生的思路，揭示整个解题的思维过程.