立足几何直观，促进数学课堂“生命化”

董秀英

几何直观是指利用图形描述几何或其他数学问题，分析、探索解决问题的思路，并预测结果。笔者认为，生命化课堂是把课堂还给学生，让课堂焕发生命活力，充分体现学生学习的自主性。借助几何直观可以把复杂的数学问题变得简明、形象，在整个教学过程中有助于帮助学生理解数学，化抽象为具体，培养学生的思维能力，促进学生主动思考和自主探索。笔者将结合自身的教学实践浅谈如何使几何直观在小学数学教学中得以有效应用，促进数学课堂生命化，从而实现对学生数学核心素养的培养。

一、借几何直观明晰算理，助问题分析，促数学课堂生命化

借助几何图形能够帮助学生更加直观地理解算理，还能够帮助学生自主发现、描述所要研究的问题，寻求解决问题的思路。“图形化”的过程就是将抽象的算法或繁杂的问题直观化。所以，借助“形”的幾何直观性可以更好地分析理解数与数之间或数量之间的关系。

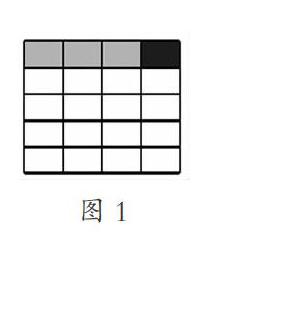
例如，分数乘法×的计算法则及算理教学。教师可以引导学生先在长方形纸中表示出1小时粉刷墙壁面的，然后让学生通过观察思考：怎样表示出小时粉刷墙壁面的几分之几？学生通过动手画图，自主探索交流，直观地理解了×的意义。先把整张纸平均分成5份，其中的1份即，将这部分再平均分成4份，这样整张纸一共平均分成20份，再涂出其中的1份就是这张长方形纸的（如图1）。学生借助几何图形的直观性，便于理解×的实际意义，也有助于掌握分数乘分数的计算方法及算理，即将分母相乘的积作为分母（先把1平均分成5份，再把分得的每一份平均分成4份，这样一共20份，就是分母），将分子乘分子的积作为分子（即表示其中的一份）。

教学中因为有了直观的几何图作为形象支撑，学生的思维被激发，主动思考的意识不断增强，解决问题的数学模型得以初步构建，最后在获得成功中体验到问题解决的喜悦，从而让数学课堂充满生命活力。

二、借几何直观发现规律，助抽象推理，促数学课堂生命化

教学中可以把几何图形与数量相结合帮助学生更形象直观地发现规律，帮助学生经历化繁为简、化抽象为具体的过程，归纳概括出数学规律，数学模型思想也初步形成。从而利用规律解决复杂的问题，使学生的抽象推理能力得以进一步提升，促进数学课堂焕发生命活力，学生的核心素养得以进一步提升。

例如，教学“20个点能连成多少条线段”这样一道题。教师引导学生讨论并提示：要研究20个点能连成的线段数量，可以先截取5个点进行试验。此举主要是向学生渗透化繁为简及有序思考的数学思想方法。学生自主动手画一画、数一数，教师引导小组合作交流发现其中的规律并板书：2个点，1条（A与B连1条）;3个点，2+1=3条（A与B、C连两条，B与C连1条）;4个点，3+2+1=6条（A与B、C、D连3条，B与C、D连2条，C与D连1条）;5个点，4+3+2+1=10条（A与B、C、D、E连4条，B与C、D、E连3条，C与D、E两点连2条，D与E连1条）（如图2）。通过取其中的一组点数作为研究对象，借助几何图形的形象直观，发现隐藏在几何图形中的规律，从而实现化繁为简的转化策略的有效渗透。根据以上的规律，20个点连成线段的问题就可以从比总点数少1的数字19开始倒加到数字1，再求和。算式：19+18+17+……+3+2+1，最后可以运用等差数列求和的方法求出结果。进而总结计算n个点连成的线段总条数模型：（n-1）+（n-2）+（n-3）+……+3+2+1=。

再如，进行+++……++教学的时候，教师可以引导学生借助图形从简单的+入手，引导学生认真观察发现：+可以看成从正方形“1”中减去空白部分的;同理可得++可以看成把剩下的再平均分成两份，这样共分成8份，其中的一份是。因此，++可以看成从正方形“1”中减去，那么+++可以看成从正方形“1”中减去（如图3）。以此类推，+++……++可以看成从“1”中减去，要求的和就转化为“1-”。

三、借几何直观感悟极限，助思维渗透，促数学课堂生命化

所谓极限思想就是用联系变化的观点，以无限逼近的方式来研究数量的变化趋势的思想。极限思想的渗透需要通过无限观念的建立和极限思想的感悟两个层面来实现，然而这两个层面的有效建立都与学生想象能力的培养密不可分。合理的想象借助几何直观的支撑，有助于帮助学生建立无限观念，促使学生真正感悟到极限思想。

例如，教学人教版六上“圆的面积”一课，教师可以引导学生发现：将圆等分切割成的扇形份数越多，每个扇形就越接近于等腰三角形，拼成的几何图形就越趋近于长方形。引导学生采用“变曲为直”“化圆为方”的转化法，让学生经历从无限到极限的过程，感悟极限思想，进一步提升学生的数学核心素养，从而促使数学课堂焕发生命活力。通过几何直观方法，学生自主探究关于圆的面积计算公式也就水到渠成。

总之，借助几何直观，可以帮助学生理解题意，分析问题并发现规律，进行抽象推理，提升思维能力，从而深刻感悟数学思想，让学生主动经历知识的形成过程，促进数学课堂跳跃出充满生机的思维火花，进而促使学生数学核心素养得到培养。

（作者单位：福建省福州市长乐区洞江小学？摇？摇？摇？摇责任编辑：王振辉）