天然河道分汊口闸段过流水流特性的试验研究

郭维东 ，杨 梓 ，林 洋 ，金明星 ，李艳朋 ，刘从坦 ，张邀丹

（1.沈阳农业大学 水利学院，沈阳 110161；2.辽宁省河库管理服务中心，沈阳 110000；3.沈阳顺源德工程咨询有限公司，沈阳 110000）

天然情况下，分汊型河道是冲积河道中较为常见的河型，具有地形、水力条件复杂，流量分配不易控制等特点，较单一河道相比，水流特性更为复杂[1-4]。实际水利工程中，发现天然河道分汊口处修建堰闸组合型拦河建筑物比较常见，有利于河道流量的分配调节，既可在洪水期有效减小对下游河道和建筑物的破坏，保证居民安全，又可在枯水期调节闸门开度来增大侧汊流量，以满足人类生产生活及生态环境的需求。目前组合型拦河建筑物的研究方向多侧重于布置形式和洪水调节[5-7]，对水流特性方面的研究较为欠缺。再鉴于，实用堰与弧形闸门横向组合型拦河建筑物是一种新型组合型拦河建筑物，对其过流研究十分必要。分汊型河道按天然河道形态一般分为顺直分汊型河道、弯曲分汊型河道、复杂分汊型河道和弓形分汊型河道。前人对分汊型河道水流特性的研究多集中于前三种河道形态，针对弓形分汊型河道的研究尚未多见。辽宁丹东某河分流堰改建工程所处河段直汊道与上游河段平顺衔接，侧汊道外形类似弯弓状，进入其中的水流与主河道成一较大交角，属于典型天然弓形分汊型河道[8-9]。鉴于此，本试验以辽宁丹东某河为原型，采用物理模型方法，研究不同工况下新型拦河建筑物闸段过流对分汊型河道水流特性的影响，分析了闸段出流规律及闸门流量系数的经验公式计算值与实测值的偏差。本次研究不仅丰富了新型组合型拦河建筑物附近的水流运动理论，也为河道整治、新型组合型拦河建筑物设计等领域起指导意义。

1 材料与方法

1.1 试验装置

本试验系统由地下水库、水泵机组、进水管、平水设施、溢水管、进水室、试验水槽、回水廊道组成[10](图1)。拦河建筑物由WES实用堰和三孔弧形闸门组合而成。试验中为达到水深要求，提高模型的精度，模型采用变态模型，根据相关规范要求，选取变态比率为2。因此，水平比尺选用λl=100，垂直比尺选用λh=50。模型采用重力相似准则设计，由于原型和模型都是处在同一重力场中，重力加速度比尺为λg=1。

图1 试验系统示意图Figure 1 Schematic diagram of test system

本试验河槽、WES实用堰及附属建筑物均采用混凝土制作完成。经计算，WES实用堰糙率为0.010。弧形闸门及闸墩等采用有机玻璃制成。WES实用堰模型堰高13.02cm，堰长325.50cm，闸室长16.00cm，闸门单孔净宽10.00cm，选定弧形闸门半径和支铰高度均为8cm。下游消力池长41.00cm，深4cm，海漫长44.00cm。

由于本次为变态模型，还需满足模型河槽与原型河槽阻力相似，因此需进行河槽表面加糙处理。通过预试验对糙率进行率定，选取实测洪痕资料对模型进行合理性验证，最终模型选用15cm×20cm尺寸防滑垫呈“品”字形摆放加糙，测定糙率为0.020[10]。河槽进水流量采用三角形量水堰进行测定，出水流量采用矩形量水堰进行测定，水深采用测针进行测量，精度为0.10mm。水流流速采用LGY-Ⅱ型便携式流速仪测记，测速范围1～300cm·s-1。

1.2 试验方案

本试验通过选取不同流量和闸门开度，对侧汊分流情况、水流特性以及闸门的过流能力进行分析。试验总流量分别选取 1500m3·s-1和 3000m3·s-1（P=20%），4600m3·s-1（临界过堰），16400m3·s-1（P=2%）。 当拦河建筑物上游水位未超过堰顶高程时，闸门开度选取0.5，1，2，3m；当超过堰顶高程时，闸门开度选取2，2.5，3m。具体工况见表1。

表1 试验工况Table 1 Experimental condition

1.3 测点布置

为方便研究在各个流量等级下试验区域的水位及流速情况，在试验过程中，干流和直汊每隔200cm设置一个测量断面，侧汊每隔100cm设置一个测量断面，共计20个断面。由于模拟天然河道，地势不平，同一断面水深不一致，流速沿横向、垂向分布不均匀，因此每隔40cm设置一个测位，每个测位依据水深情况垂向布置1～4个测点。为研究拦河建筑物附近水流特性和闸门过流情况，在拦河建筑物附近设置了6个断面，分别位于上游距堰26.45cm处、堰上、消力池前、消力池后、海漫前、海漫后，每个测流断面设置了12个测位，具体布置位置如图2。

图2 拦河建筑物附近测位布置图Figure 2 The arrangement diagram of position measurement near river barrage

2 结果与分析

本次试验由于地形、水位等因素的限制，选用了变态比尺进行模型设计及试验测定，为直观清晰得出各工况下物理参数的对比分析，将模型试验所测参数经比尺换算为原型参数后再进行研究分析。

2.1 侧汊分流比

对于分汊型河道来说，侧汊分流比是河道整治中的一个重要参数，其数值变化影响着河道安全、防洪建设及人类生活等，因此，在侧汊分汊口布置拦河建筑物，有利于控制过流流量、调节水位。本次试验WES实用堰堰高为定值，闸门开度和上游来流流量是侧汊分流比的重要影响因素，侧汊分流比的计算采用了丁君松方法[11]，计算公式为：

式中：Q直、Q侧分别为直、侧汊流量；η侧为侧汊分流比。

图3给出了本次试验各工况下，侧汊分流比η侧随闸门开度e的变化关系。在小流量工况下，即上游水位未超过堰顶高程，侧汊分流比较小，水流主要从直汊流出，随闸门开度的增大，侧汊分流比逐渐增大，且流量越小，增幅越大。在闸门开度相同时，流量越大，侧汊分流比越小。这是由于此种工况下，拦河建筑物堰段只发挥了挡水作用，侧汊水流全部从闸段通过，过流断面受到限制，随着来流总量的增加，侧汊过流流量增加，但增幅较小，侧汊分流比减小。当流量增大至16400m3·s-1时，侧汊分流比较大，且发现随闸门开度的增大，侧汊分流比基本保持不变。其原因在于此工况拦河建筑物全断面过流，主流线位于堰段侧。当闸门开度小时，壅高上游水位，堰段过流能力增大；闸开度增大，上游水位降低，堰段过流能力减小，此时闸段过流能力增加。此外，闸相对于堰来说，调节流量效果较好，容易控制。

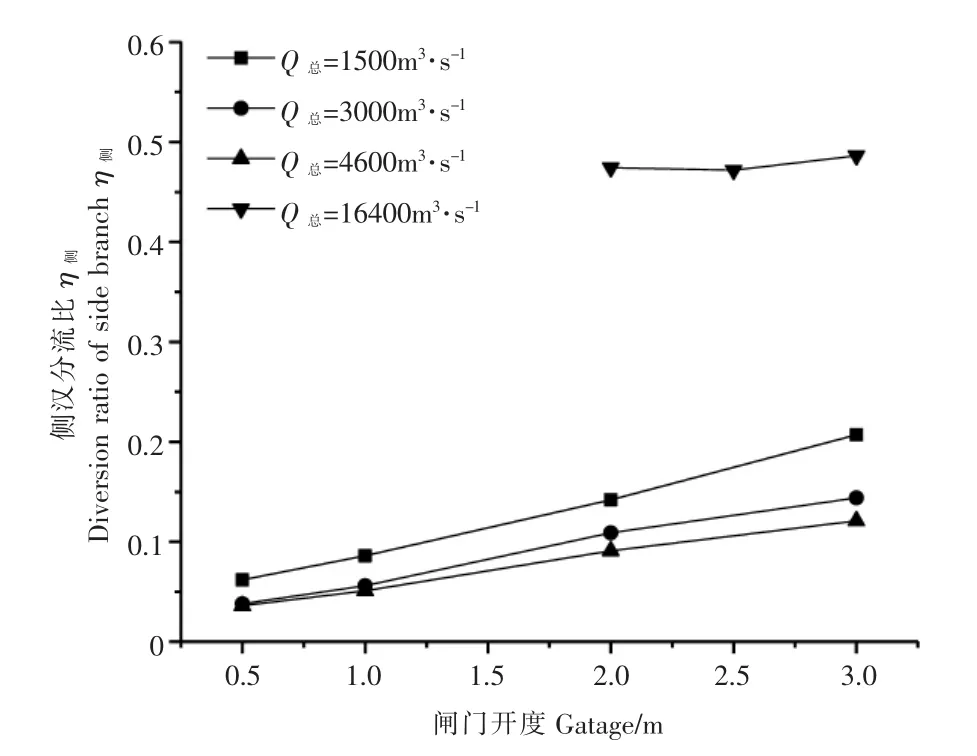
图3 侧汊分流比η侧与闸门开度、流量的关系Figure 3 Relationship between diversion ratio of side branch ηsideand gatage and flow

2.2 拦河建筑物附近水位及流速分析

2.2.1 水位分析 根据图4中的各工况水位分布图可看出，由于复杂的地形条件和水力条件，拦河建筑物上、下游水位分布不均，水流流经闸门，水位下降，其后受消力坎作用，在消力池内水位壅高，进而达到消能作用，且闸段侧壅高较为明显。在小流量工况下，水流仅通过闸门流入下游，因此水流在闸后发生扩散，流量越大，扩散范围越广，左右岸存在明显水位差。由图4可知，在相同流量下，随闸门开度增加，下游水位增高，上、下游水位差略微减小。在同一闸门开度条件下，随流量增加，上游水位最高点向闸段侧偏移，下游水位增高，上、下游水位差明显增大。

上游水深和闸门开度是影响闸门水力特性的重要因素，图5分别给出了本试验9个工况下的上游水深h与总流量Q总、闸门开度e的关系。由图5a可知，闸门开度一定时，上游水深随流量增加呈线性增长，且闸门开度为2m工况下的增长速率大于开度为1m、3m工况。由图5b可知，流量不变时，上游水深并非随着闸门开度的增加而增加。在流量为1500m3·s-1时，随闸门开度逐渐增大，上游水深呈先减小后增大的趋势；在流量分别为3000m3·s-1和4600m3·s-1时，随闸门开度的逐渐增大，上游水深均呈先增大后减小的趋势，但在3000m3·s-1流量工况下，上游水深浮动范围非常小。因此，本试验发现在流量为3000m3·s-1附近，存在一个临界流量，使得上游水深不随闸门开度的变化而变化，为一常数。

2.2.2 流速分析 由图6可知，上、下游闸段侧平均流速均大于堰段侧，水流过闸流速骤增，经消力池流速逐渐减小，在消力坎前 K21、K22、K23、K31、K32、K33工况的流速均减至 2m·s-1以下，最大流速存在于工况 K13，为 2.89m·s-1。在消力坎处过流断面收缩，闸侧流速存在增大趋势，经海漫后水流恢复平稳，各工况流速均不足2m·s-1。在闸门开度相同下，随流量增大，上游流速峰值向闸段侧偏移，且峰值增大。在总流量为1500m·s-1和3000m·s-1情况下，随闸门开度增大，上游流速峰值向闸门侧偏移，且峰值也增大。这是由于上游来流方向与建筑物轴线不正交，堰侧水流存在向闸侧流动的趋势，且闸门开度增大趋势增强，流速增大。在总流量4600m·s-1情况下，上游流速峰值均发生在闸前。

图4 拦河建筑物附近水位分布图Figure 4 The diagram of water level distribution near river barrage

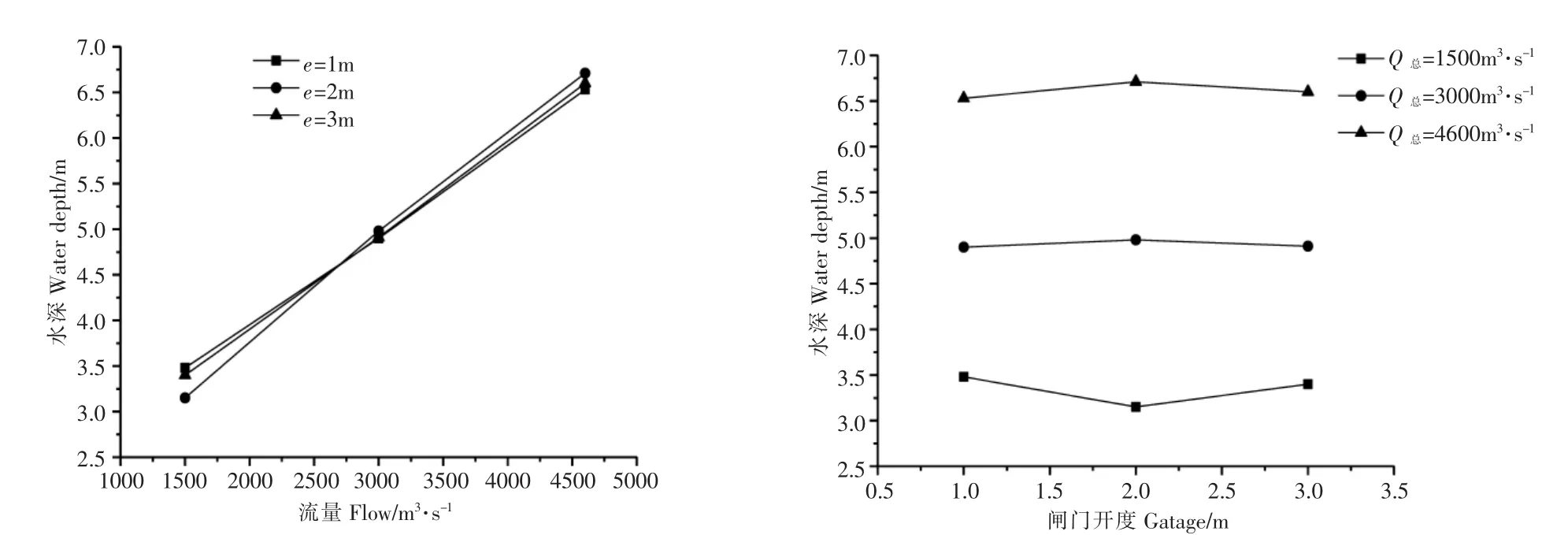
图5 上游水深随总流量、闸门开度的变化关系Figure 5 The relationship between upstream water depth and total flow and gatage

2.3 流态分析

水流通过闸门流入消力池进行消能，且伴有表面旋滚及强烈紊动现象（图7）。水流在导流板后发生扩散，导流板右侧产生回流区。其原因在于闸后水流受导流板的导流作用和自身的惯性作用，水流进入消力池后不会立即扩散，仍会继续压缩水体，但速率减慢，产生压力梯度，形成回流。水流向前行进一小段距离后将发生扩散，直到全断面。

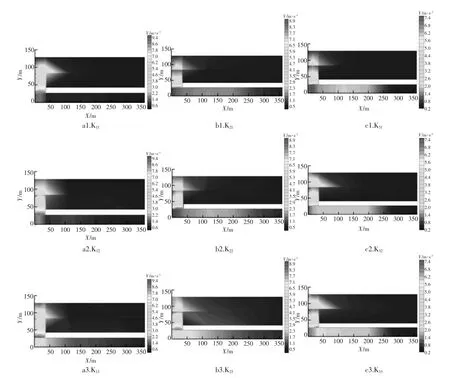
图6 拦河建筑物附近流速分布图Figure 6 The diagram of velocity distribution near river barrage

2.4 闸后消能效果分析

本试验闸后水流下泄流速较大，9种工况下的弗汝德数Fr均大于1，为急流。下游水流处于缓流状态，流态过渡必然产生水跃，采用消能方式为底流消能。根据王冰洁[12]的研究，由图8可知，在闸门开度相同时，流量越大，闸后消力池内Fr越大，消能效果越好。在总流量为4600m3·s-1和3000m3·s-1时，随闸门开度的增大，消力池内Fr越大。当总流量减小到1500m3·s-1时，随闸门开度的增大，消力池内Fr越小。这种现象是由于闸后扩散比较大，且存在水头损失。当闸门开度一定时，总流量增大，闸门上、下游水位差增大，闸门过流能力增强。

在工况K11、K12、K13下，Fr在2.5～4.5范围内，发生不稳定水跃，跃后水流波动较大，并向下游传播，消能率小于 20%。 在工况 K21、K22、K23、K31、K32、K33下，Fr在 1.0～1.7 范围内，此时为波状水跃，水面形成微弱起伏的水波。

2.5 闸门流量系数的分析

根据e/H大小判别闸门的出流形式，发现仅有K33工况时，e/H值大于0.65，为堰流，其他工况均为闸孔出流。通过比较下游水深ht与临界跃后水深hc＇＇的大小，确定本试验条件均为自由出流，淹没系数σs取1.0。由能量方程推导可知，闸门流量系数是闸孔流速系数与过闸水流收缩系数的乘积，与闸孔水头损失、水流收缩程度、收缩断面流速分布等有关[13]。

图7 闸后流态图Figure 7 Flow pattern behind sluice gate

（1）南京水利科学研究院的经验计算公式[13]：考虑到闸门相对开度e/H和闸门底边缘切线与水平线夹角是影响水头损失和水流垂向收缩的直接因素。

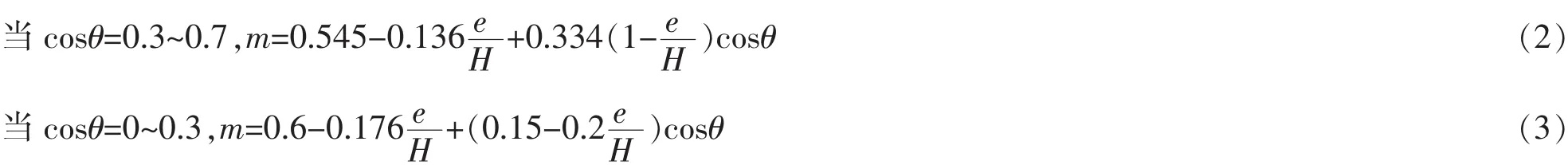
式中：θ为闸门底边缘切线与水平线夹角；e为闸门开度；H为闸上水头。此计算公式适用范围为0＜e/H＜0.5，0＜cosθ＜0.7。

（2）Henry计算公式[14]。在自由出流条件下，经分析拟合得流量系数与上游水深和闸门开度函数关系式：

式中：H0为上游水深。此公式是在静水压力分布的假设下得出的，忽略了流速水头，未考虑闸门底边缘切线与水平线夹角对流量系数的影响。

（3）《水力学》计算公式[15-16]。基于能量方程，经研究得闸门相对开度e/H和闸门底边缘切线与水平线夹角θ是影响闸门流量系数的主要因素。通过试验数据分析得到经验公式：

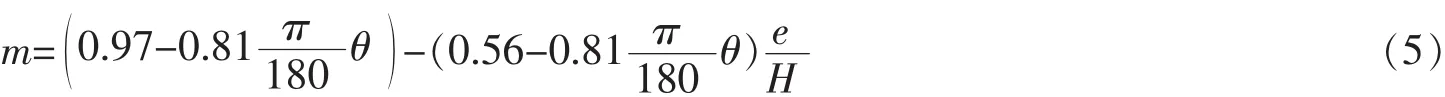
此计算公式适用范围为 0＜e/H＜0.65，25°＜θ＜90°。

本研究利用试验数据对闸门流量系数的现行公式进行了精度检验。根据表2和图9中数据显示，南京水科院经验公式的计算值均在±10%误差范围内，但此公式仅适用于计算本次试验方案数据的37.5%，局限性较大；《水力学》经验公式计算值在±10%误差范围内的数据占62.5%，在闸门开度为2m和3m时，本公式计算误差较小；Henry公式计算值在±10%误差范围内的数据占75%，计算值与另外两种公式计算结果相比较小，在总流量为1500m3·s-1和3000m3·s-1时，计算误差较小。研究表明，由于本次试验条件地形的复杂性，闸门开度越小，现行公式的计算结果差异性越大，现行公式中无一能够较准确地计算本试验闸门的流量系数。决定堰闸等低水头过流建筑物起过流能力大小的流量系数不但受到下游水位形成的淹没度等因素影响，也受闸墩体型及侧收缩等因素的影响。本试验条件为自由出流，闸前单侧收缩比远大于1.0，对闸孔水头损失及流速分布产生直接影响。为得到准确的闸孔过流流量，引入闸孔侧收缩系数ε对Henry公式进行修正：

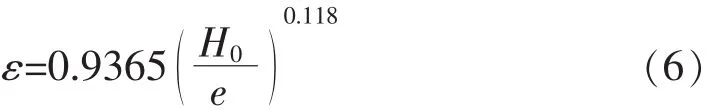
此时，用εCd代替Cd，得到修正后的流量系数Cd。本公式适用于堰闸横向组合型建筑物闸侧过流条件，主流线于闸前从堰侧偏转至闸侧，且0.15＜e/H0＜0.65。由图10可见，修正公式的所有计算值均在±10%误差范围内，与原公式相比，结果较为精确。

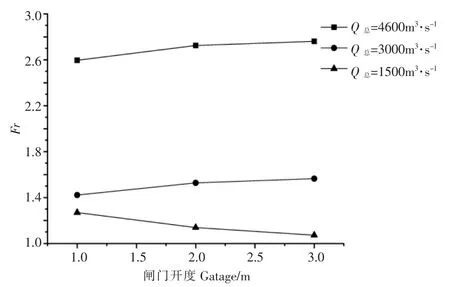
图8 弗汝德数随闸门开度的变化曲线Figure 8 The curve of Froude number versus gatage

图9 各公式流量系数计算值与实测值的比较Figure 9 Comparison between calculated values of discharge coefficient for various formulas and measured values

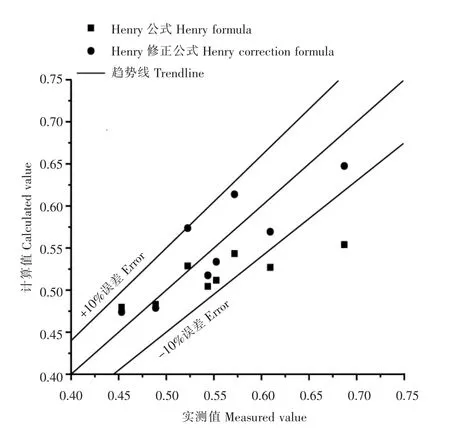
图10 修正公式与现行公式流量系数计算值的比较Figure 10 Comparison between calculated values of discharge coefficient for corrected formula and current formula

3 讨论与结论

在河道治理过程中，分汊河道上修建工程对其分流比有一定影响。杨胜发等[17-18]均采用物理模型的方法，分别讨论了上游码头和丁坝的布置位置对分流比的影响，建筑物自身不可调节，分流比不易控制。郭维东等[19-21]分别采用了数学模型和物理模型的方法，分析了分流比对弯道及引水口水流的水面线及流速分布等的影响。本研究特点在于采用了一种新型组合型拦河建筑物，使流量得到很好的控制，消能方式为底流消能。经对比分析，闸段单侧过流时，侧汊分流比明显小于全断面过流，且拦河建筑物上游水位、流速分布不均。闸门开度一定，上游水深随流量增加呈线性增长，且闸门开度2m工况增长速率大于开度3m工况增长速率，开度3m工况增长速率大于开度1m工况增长速率。此外，研究发现利用各现行公式计算的流量系数不大相同，均与实测值存在偏差，因公式的试验条件与推导方法不同，会对闸门过流能力的计算产生影响[22]。

本研究结果表明，闸段单侧过流条件下，水流过闸在消力池内发生表面旋滚及扩散，产生回流区。流量一定，随闸门开度增大，侧汊分流比增大，且流量越小，增幅越大；闸门开度相同，流量越大，侧汊分流比越小，闸后消力池内Fr越大，消能效果越好，且上游水位最高点向闸段侧偏移，在3000m3·s-1流量附近，存在一个临界值，使得上游水深不随闸门开度的变化而变化。随流量增大，闸门开度增大，上游流速峰值向闸段侧偏移。本研究引入闸孔侧收缩系数ε对现行公式进行修正，该修正公式的计算值均在±10%误差范围内，结果令人满意。现行公式存在一定局限性，要得到准确的流量系数，还需根据具体条件进行试验校核及修正，确保实际工程安全性的同时，经济效益最大化。