基于WPA优化神经网络的扼流适配变压器故障诊断研究

郑云水，李程



基于WPA优化神经网络的扼流适配变压器故障诊断研究

郑云水，李程

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

针对传统铁路扼流适配变压器故障诊断模型结构复杂和精度不高的问题，运用狼群算法(WPA)、粗糙集(RS)理论和神经网络(NN)相融合的方法对其进行故障诊断研究。用粗糙集理论对故障样本数据进行约简处理，减少样本数据的监测及关键特征量的输入个数；利用约简后的数据对神经网络训练。利用狼群算法优化BP神经网络参数，提出WPA-BPNN故障诊断模型，以侯马电务段扼流适配变压器故障数据为例进行验证。研究结果表明：WPA-BPNN故障诊断模型相比传统方法，简化了网络结构，缩短了训练所需时间，提高了故障诊断精度，保证了列车行车安全及线路的高效运行。

扼流适配变压器；故障诊断；粗糙集；狼群算法；神经网络

扼流适配变压器已被广泛使用在我国的电气化铁路中，是站内轨道电路的重要组成设备，安装于强弱电结合部位，为牵引电流和信号电流回流提供通路[1]；对不平衡电流给轨道电路正常作业造成的影响具有明显的抗干扰作用，确保列车行车稳定、安全、可靠非常重要。由于扼流适配变压器本身结构的复杂性及作业环境的多变性，当其出现故障时导致“红光带”现象频繁发生。铁路扼流适配变压器出现故障时，单纯地依靠工作人员的维修经验，已不能满足时代发展的需求，因为其不能快速、准确地定位故障发生的位置及故障发生的原因，严重影响了线路营运效率和行车安全。王惠中等[2−3]指出，随着人工智能、信息化技术的不断进步，智能故障诊断技术快速发展，现已广泛应用于铁路信号设备故障诊断领域中，逐步取代了人工排查故障的手段，如利用蝙蝠算法、粒子群算法、神经网络等算法和技术，其可单独使用也可与其他算法相结合，使得故障诊断的网络性能更加优化，从而保证了故障诊断准确率和效率[4]。工作状态可分为调整状态、分路状态；选取某线路区段逐步测量并记录扼流适配变压器13个考察点的电压电流。故障诊断的核心是对现场采集数据关键特征值的准确提取，本文用粗糙集理论对采集到的故障样本数据进行处理；为了改善神经网络的缺陷，用WPA优化BP网络的结构，然后利用RS处理过的样本对WPA-BPNN模型进行训练。最后，Matlab仿真结果表明经WPA优化的BP网络，其训练效率和收敛速度有了明显提高，使得故障诊断结果更加精确，验证该了算法较其他算法的高可靠性和有效性。

1 扼流适配变压器故障诊断样本数据表

根据现场工作人员的维修经验，并通过查阅扼流适配变压器故障诊断方面的相关资料，得到扼流适配变压器时常发生的12种故障，如图1所示。引用文献[5]中离散化后的故障诊断样本数据表，如表1所示，对其进行故障诊断研究。

{1，2，…，15，16}表示扼流适配变压器的16种故障类别集；GJ为轨道继电器两端的电压，RG受电端轨面电压，TG送电端轨面电流，RG受电端轨面电流，TG送电端轨面电压，RS受电端信号侧电压，TS送电端信号侧电压，RS受电端信号侧电流，TS送电端信号侧电流，RL受电端适配器电感电压，U送电端适配器电感电压，U受电端适配器电容电压，TC送电端适配器电容电压，={GJ，TS，RG，…，TL，RG，TC}表示扼流适配变压器所对应的13种故障特征的征兆集。

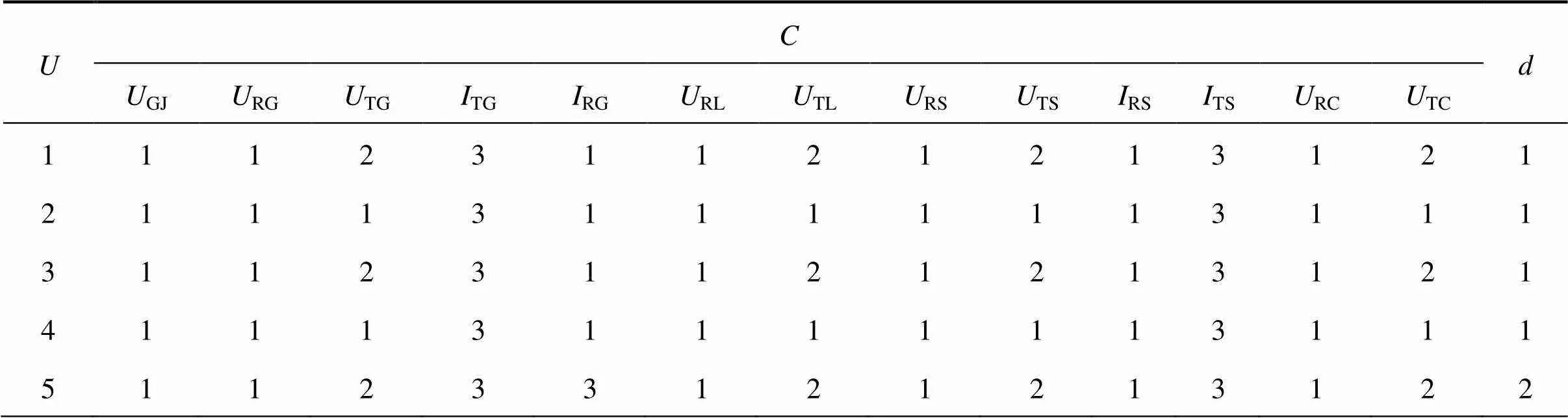
表1 扼流适配压器故障诊断样本数据表

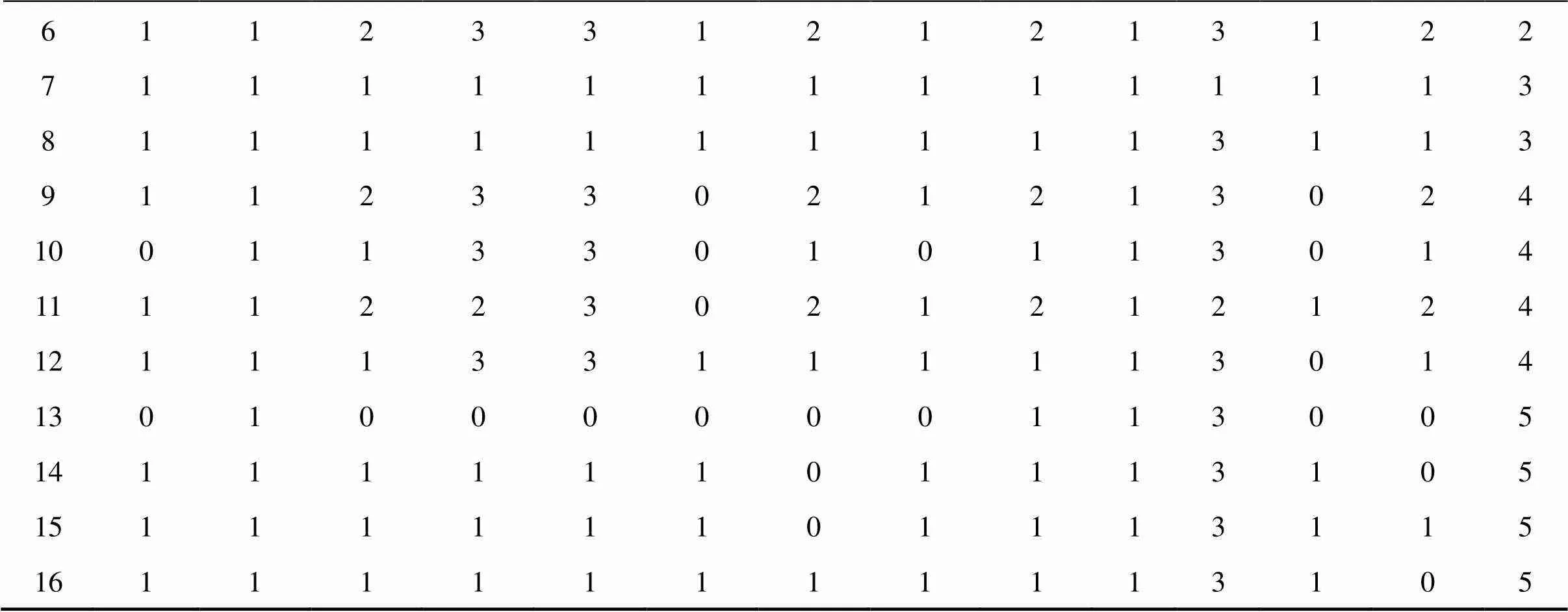
611233121213122 711111111111113 811111111113113 911233021213024 1001133010113014 1111223021212124 1211133111113014 1301000000113005 1411111101113105 1511111101113115 1611111111113105

2 扼流适配变压器故障诊断的规则约简

2.1 粗糙集理论

粗糙集RS(Rough Set)理论是一种能有效的处理各种不完备信息的数学工具[6]，不用提前给其赋予某些定性或定量的特性来描述指定的方法模型，而是根据粗糙集理论本身的结构和特点，直接利用所给问题本身的数据并结合其自身强大的自学习组织能力直接对样本数据进行分析和推理，挖掘出数据间隐含的一些潜在的逻辑和规则，从而提炼出有价值的信息，是一种简化处理信息的方法[7]。

2.2 决策属性分析

由于扼流适配变压器自身结构的复杂性，故对其工作模式只划分了正常状态和故障状态。当其发生故障时，首先要判断故障发生的具体位置(是受电端还是送电端)，然后分析出故障原因(是牵引线圈故障或是适派器故障)，最后根据相应的诊断结果进行处理。现设置了以下5种决策属性：1) 正常状态(其中包含0.06分路状态和0.15分路状态，记为1)；2) 受电端牵引线圈故障(记为2)；3) 送电端牵引线圈故障(记为3)；4) 受电端适配器故障(记为4)；5) 送电端适配器故障(记为5)。

2.3 相对属性约简

为了更加精确的提取故障诊断的关键特征值，用粗糙集理论设计相对属性约简算法，对表1的故障样本数据进行约简[8]。

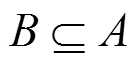
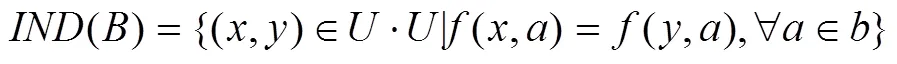
称()为属性集的不可分关系，可用R符号来表示。其中：为条件属性集；为决策属性集；为属性的值域；为信息函数，是对象中属性到值域的映射。

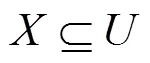
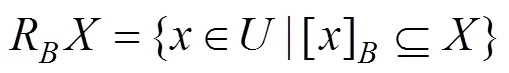
2) |{UGJ}()|=0,|{URG}()|=0, |{IRG}()| =1,…, |{UTL}()|=3, |{UTC}()|=3, Redu=Redu+TL={TL},=−{TL}={GJ,RG,RG,…,TS,TC}；

4) |{UTL, IRG, URL, URC, UTG, UGJ}()|=14,…,|{UTL, IRG, URL, URC, UTG, UGJ}()|=16, Redu=Redu+TL={TL,RG,RC,TG,TC},=−{TC}={GJ,RG,…,TS,TS}；

经过上述一系列属性约简，得到最优扼流适配变压器故障诊断决策表，如表2所示，从表中可得知最终用于本设备故障诊断的关键特征值Redu= {RG,RL,RC,TG,TL,TC}。

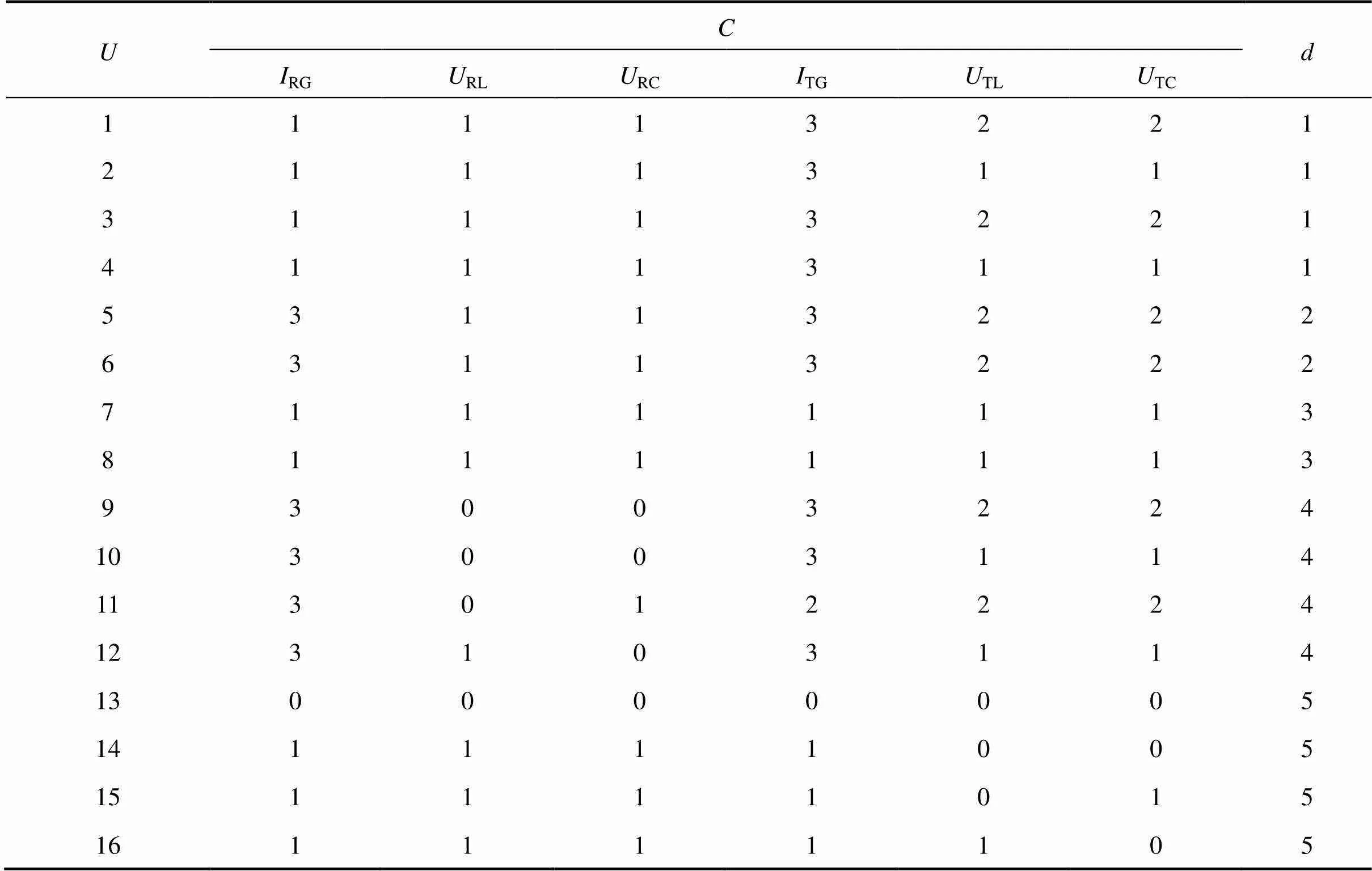
表2 最优扼流适配变压器故障决策表

当送受电端监测物理量选取一致时，经上述算法约简得到的关键特征量作为狼群算法优化BP神经网络的输入的最优结果。在Matlab仿真中对该算法进行仿真处理，可得出结论：依据RG,RL,RC,TG,TL和TC这6种特征关键量作为诊断系统输入，可辨别扼流适配变压器所有的故障类型，满足故障诊断的要求。

3 狼群算法优化BP神经网络

3.1 BP神经网络拟合函数的原理

图2中，[1,2,…, X]和[1,2,…,Y]分别表示BP神经网络的输出层输入量、输出层的运算值，w表示输入层到隐含层的连接权值，b则表示BP神经网络隐含层节点输出阈值[9]。

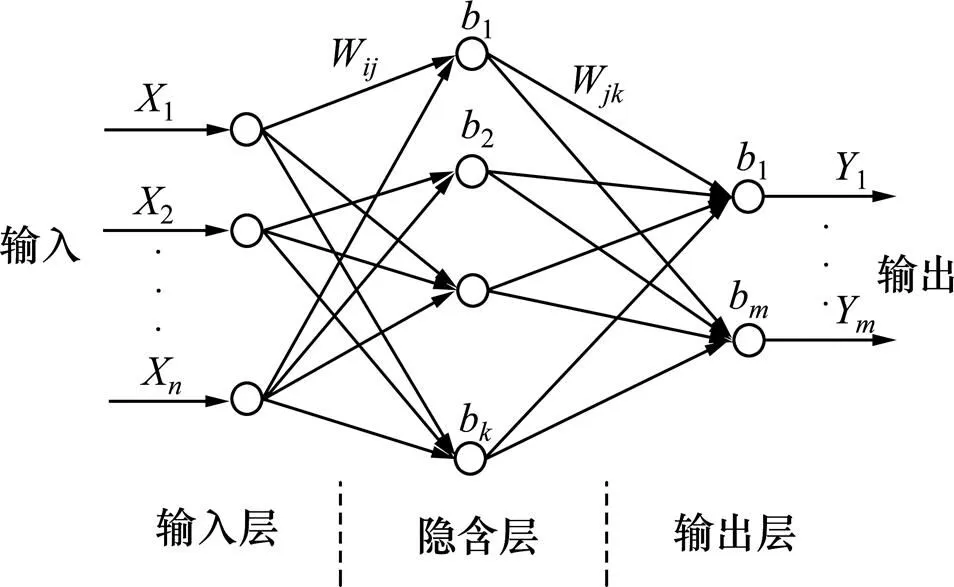
图2 BP神经网络拓扑结构图

3.2 狼群优化算法

狼群算法是从自然界狼群生活习性及其协作捕猎活动的基础上提出的一种新的群体智能算 法[10]。算法的主体是模拟狼群分工协作的4个过程，即由狼群个体的游走、召唤、围攻和食物分派。本算法中，游走行为体现了狼个体依据自身能力，对其当前所在位置附近局部最优值的搜寻；召唤行为体现了头狼对整个狼群的决策领导能力[11]；围攻行为狼群利用群体中最优个体狼信息搜寻全局最优值；而食物分派过程体现了狼群中按劳分配的机制，这样就有效地保证了最优个体狼的生命力，促使狼群多样性从优延续，这样就从源头上避免了算法陷入局部最优解[12]；同时狼群算法的求解过程中，不管是从选择的方法还是求截域上，都能够较好地兼顾对解空间的全局寻优和局部开发，从而使狼群算法最优解的问题最终转化为狼群位置确定的问题，更加明确地体现了狼群算法具有优良的寻优性能。

3.3 狼群算法优化BP神经网络步骤

狼群算法主要针对BP神经网络的权值和阈值进行优化，将狼群算法中的个体狼前后2次位置的变化与BP神经网络的权值和阈值建立对应关系，编码成种群中的狼个体[13]。将狼所感知猎物的最小气味浓度值对应的个体狼的位置，赋给BP神经网络的初始权值和阈值[14−15]。狼群中某个体狼的迭代寻优，对应着神经网络权值和阈值的更新，同时搜寻出最优个体狼位置就可得网络的最优权值和阈值，从而达到优化神经网络的目的。最后将样本数据输入优化后的BP神经网络进行训练。主要步骤如下。

1) 狼群初始化：设在维搜索空间中，人工狼数量为，个体狼最大迭代次数为max，最大游走次数为max，步长因子，距离判定因子，狼群更新比因子，探狼比因子为，其中第只人工狼的位置状态为：

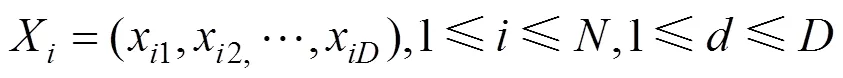
2) 确定气味浓度函数。将函数的实际输出值和预测值的差值作为人工狼感知的气味浓度函数，计算公式为

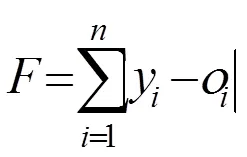
式中：神经网络的输出层节点个数为；y和o分别表示第个节点的实际输出值、预测输出值。

通过目标函数可计算出狼群中所有狼感知猎物气味浓度，依据目标函数值的大小，将狼群划分为头狼、探狼和猛狼。

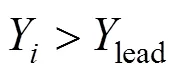
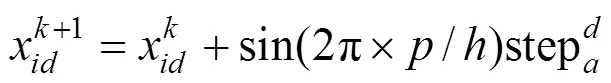
5) 围攻行为。以围攻的猎物为中心按式(6)对狼群位置进行更新。

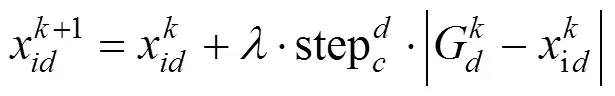
式中：取[−1,1]间的自然数；stepc为围攻步长。

6) 输出全局最优狼位置，与网络权值和阈值建立映射关系；将最优权值和阈值作为BP神经网络学习优化的参数，进行故障诊断看能否满足误差要求。算法流程如图3所示。

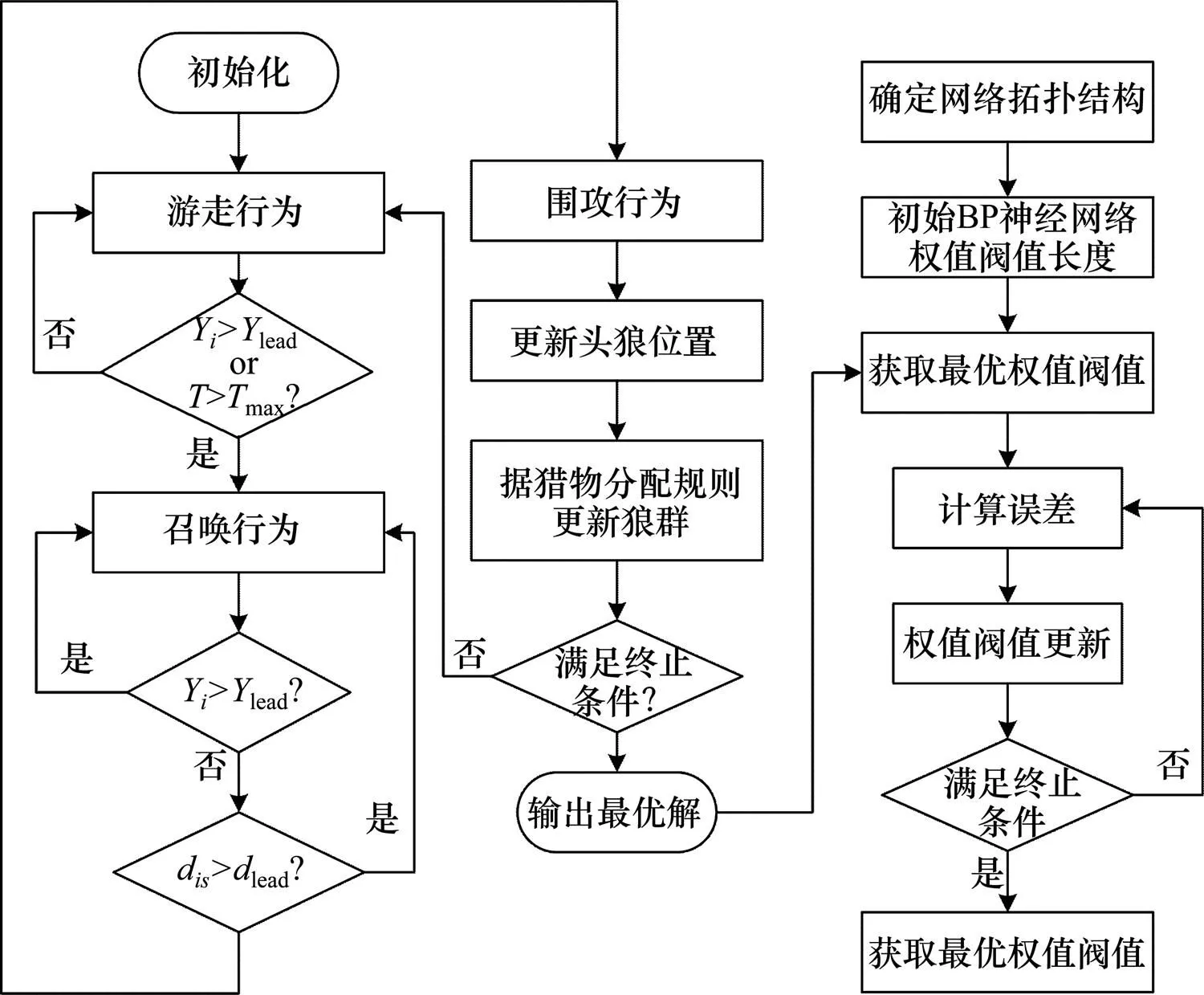
图3 WPA优化BP神经网络流程图

3.4 WPA优化BP神经网络故障诊断

WPA-BPNN模型中，经过粗糙集对样本数据处理，由表2可知输入层神经元的参数为6；输出层神经元的参数为5；经过多次仿真比较，当隐含层节点数为7时，神经网络对函数的拟合曲线效果最好，故WPA-BPNN中隐含层的节点个数取7；由此可得到WPA-BPNN模型结构为6-7-5。

应用Matlab实现WPA-BPNN训练仿真，设置BP神经网络的最小训练误差平方和为0.000 1，训练次数的上限为100，初始学习速率为0.01，动量常数=0.92；现从侯马电务段现场实际监测的数据中随机选取180组样本中的150组作为训练学习样本数据，实验可得WPA优化的神经网络参数设置如下：狼群的种群数量=200，max=100，max=20，=4，=6，=500，=1 000。为验证此故障诊断设计的高效性，用余下的30组作为测试样本数据，如表4所示。

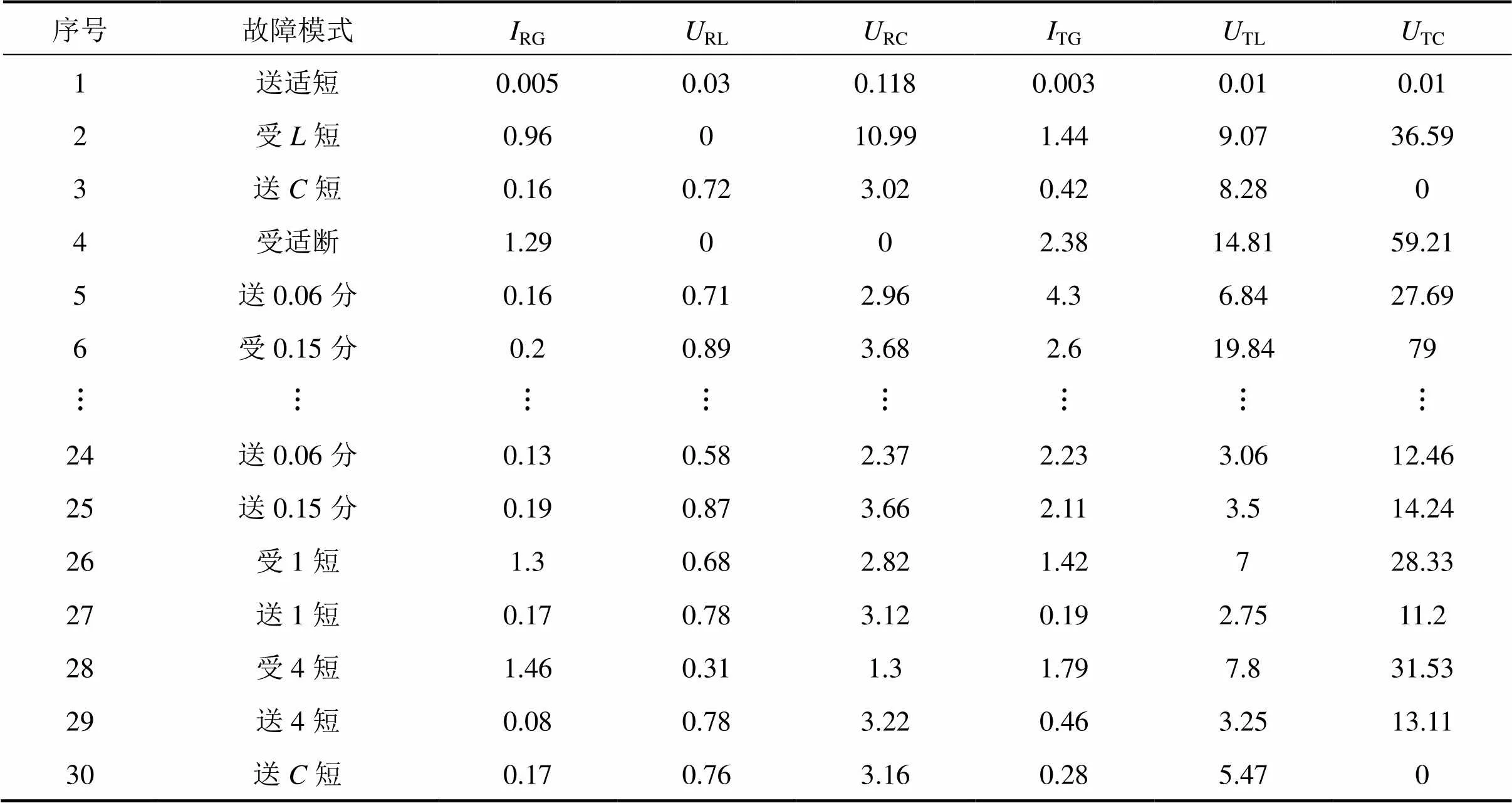
表4 故障数据实例表

通过图4对比可知，在100次内的训练中，经WPA优化的神经网络相比原始神经诊断网络，速度及精度有了明显的提高，满足预期设定的目标输出；图4(a)表示原始的网络需86步学习训练后才能收敛，而图4(b)显示出经WPA优化的神经网络只需47步。仿真结果表明，WPA不仅优化了BP神经网络的结构同时缩短了训练所需时间，使网络的收敛速度更快，提高了故障诊断精度，充分显示了其优越性。

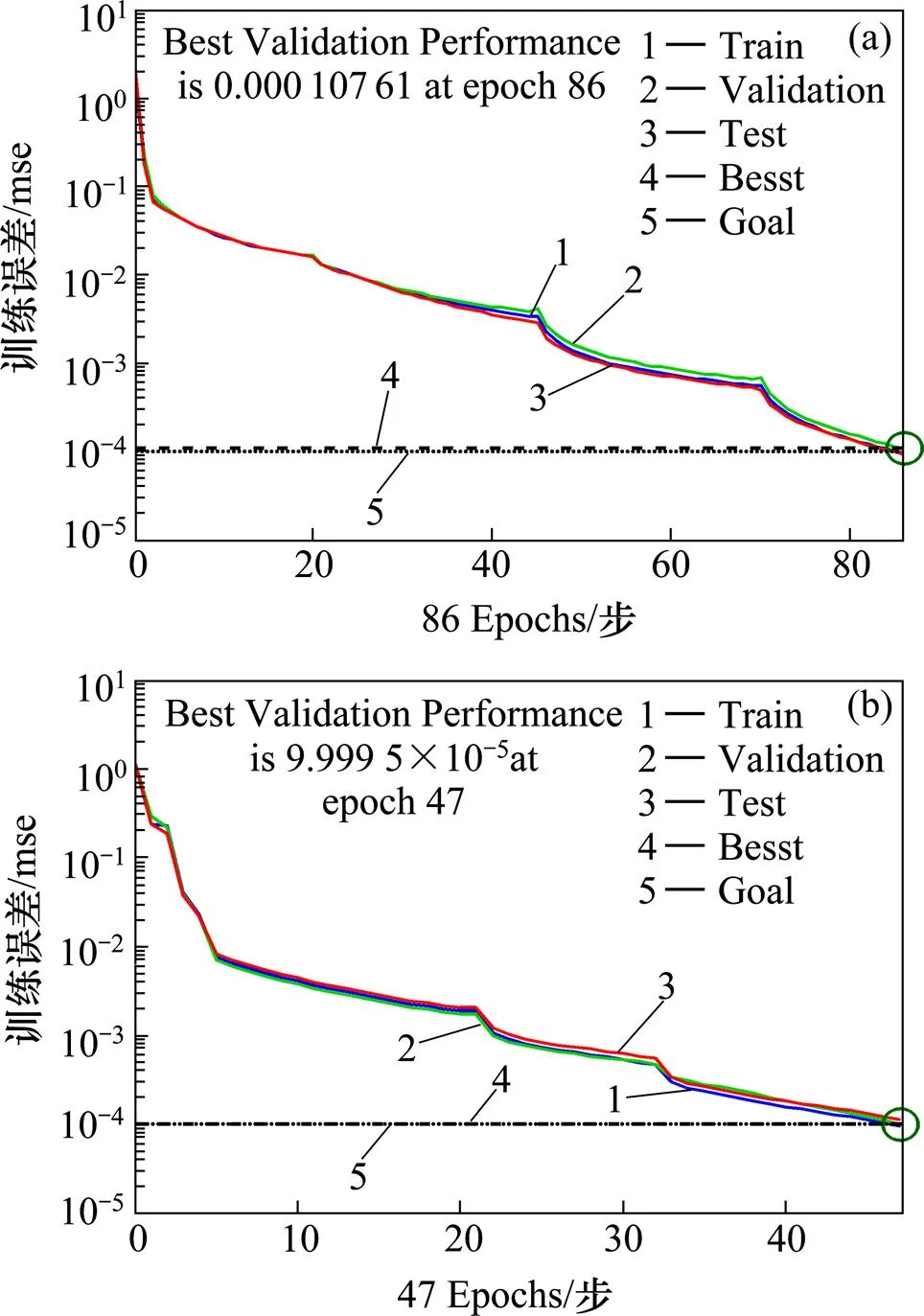
(a) 神经网络训练输出误差曲线；(b) WPA优化后的网络训练输出误差曲线

4 结论

1) 针对扼流适配变压器故障诊断，运用粗糙集理论对其大量的现场故障样本数据进行预处理，提取特征值，使得输入BP神经网络节点的特征值数大大减少；引入狼群算法，利用狼群算法良好的全局搜索能力对神经网络的相关参数进行优化，从而避免了BP神经网络陷入局部极小值；最终构建狼群算法优化神经网络的WPA-BPNN故障诊断模型，提高了BP神经网络的学习效率及故障诊断准 确率。

2) 通过现场实际数据仿真结果表明：本文设计的方法提高了扼流适配变压器故障诊断精度，验证了其可行性和高效性，为更近一步研究铁路扼流适配变压器故障诊断可选择性。

3) 构建的WPA-BPNN故障诊断模型对扼流适配变压器进行故障诊断，有效地保证了铁路基础设备的安全性能，提高了铁路运营效率，是一种可行可靠的故障诊断方法。

[1] 季广港, 武晓春. 扼流适配变压器等效电路模型研究[J]. 制造业自动化, 2017, 39(8): 127−130.JI Guanggang, WU Xiaochun. Research on equivalent circuit model of choke adapter transformer[J]. Manu- facturing Automation, 2017, 39(8): 127−130.

[2] 王惠中, 夏雨婷, 乔林翰, 等. 关于电机故障诊断方法的优化研究[J]. 计算机仿真, 2017, 34(6): 361−366.WANG Huizhong, XIA Yuting, QIAO Linhan, et al. Optimization studies of motor fault diagnosis method[J]. Computer Simulation, 2017, 34(6): 361−366.

[3] 张友鹏, 常高武, 赵斌. 基于SA算法的无绝缘轨道电路故障综合检测方法[J]. 铁道学报, 2017, 39(4): 68−72.ZHANG Youpeng, CHANG Gaowu, ZHAO Bin. A comprehensive fault detection method for jointless track circuit based on SA algorithm[J]. Journal of the China Railway Society, 2017, 39(4): 68−72.

[4] 陈星, 董昱. 基于模糊认知图模型的轨道电路故障诊断[J]. 铁道科学与工程学报, 2017, 14(9): 1983−1989.CHEN Xing, DONG Yu. Track circuit fault diagnosis based on fuzzy cognitive map model[J]. Journal of Railway Science and Engineering, 2017, 14(9): 1983−1989.

[5] 张楠乔, 杨世武, 徐宗奇, 等. 基于粗糙集和模糊推理的高铁扼流适配变压器故障诊断研究[J]. 铁路计算机应用, 2017, 28(4): 1−5.ZHANG Nanqiao, YANG Shiwu, XU Zongqi, el at. Fault diagnosis of choke adapter transformer based on rough set and fuzzy inference for high-speed railway[J]. Railway Computer Application, 2017, 28(4): 1−5.

[6] 陈覃霞, 刘盾, 梁德翠. 粗糙集理论和信息熵的AHP改进方法[J]. 计算机科学与探索, 2018, 12(3): 484−493.CHEN Qinxia, LIU Dun, LIANG Decui. Improving AHP approach based on rough set theory and information entropy[J]. Journal of Frontiers of Computer Science & Technology, 2018, 12(3): 484−493.

[7] Ma M, Chakraborty M K.Covering-based rough sets and modal logics. Part II[J]. International Journal of Approximate Reasoning, 2018, 77(14): 55−65.

[8] JING S Y, LI G L, ZENG K, et al. Efficient parallel algorithm for computing rough set approximation on GPU[J]. Soft Computing, 2018(10): 1−17.

[9] 潘庆先, 董红斌, 韩启龙, 等. 一种基于BP神经网络的属性重要性计算方法[J]. 中国科学技术大学学报, 2017(1): 18−25.PAN Qingxian, DONG Hongbin, HAN Qilong, et al. A method of attribute importance calculation based on BP neural network[J]. Journal of China University of Science and Technology, 2017(1): 18−25.

[10] 薛俊杰, 王瑛, 李浩, 等. 一种狼群智能算法及收敛性分析[J]. 控制与决策, 2016, 31(12): 2131−2139.XUE Junjie, WANG Ying, LI Hao, et al. A smart wolf pack algorithm and its convergence analysis[J]. Control and Decision, 2016, 31(12): 2131−2139.

[11] LI H, WU H. An oppositional wolf pack algorithm for parameter identification of the chaotic systems[J]. Optik- International Journal for Light and Electron Optics, 2016, 127(20): 9853−9864.

[12] ZHU Aijun, XU Xuanpei, LI Zhi. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 317−328.

[13] 颜学龙, 丁鹏, 马峻. 基于狼群算法的RBF神经网络模拟电路故障诊断[J]. 计算机工程与应用, 2017, 53(19): 152−156.YAN Xuelong, DING Peng, MA Jun. Analog circuit diagnosis based on wolf pack algorithm radical basis function network[J]. Computer Engineering and Applications, 2017, 53(19): 152−156.

[14] Komaki G M, Kayvanfar V. Grey wolf optimizer algorithm for the two-stage assembly flow shop scheduling problem with release time[J]. Journal of Computational Science, 2015(8): 109−120.

[15] 范斌, 刘辉, 汪繁荣, 等. 狼群算法优化BP神经网络的电缆故障测距算法[J]. 云南大学学报, 2016, 38(6): 873−878.FAN Bin, LIU Hui, WANG Fanrong, el at. Cable fault location method based on wolf pack algorithm and BP network[J]. Journal of Yunnan University, 2016, 38(6): 873−878.

Fault diagnosis research for choke adaptor transformer based on WPA optimizing neural network

ZHENG Yunshui, LI Cheng

(School of Automatic & Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to solve the problem that the fault diagnosis model of the traditional railway Choke adaptor has the complex structure and the low precision, this paper used the WPA (Wolf Pack Algorithm), RS (Rough Sets) theory and neural network (NN) methods to do research on the fault diagnosis. The RS theory was used to reduce the fault sample data, the sample data monitoring and the number of key feature inputs; then the neural network was trained by using the reduced data. Finally, the parameters of BP neural network were optimized by wolves algorithm, and the WPA-BPNN fault diagnosis model was proposed. Fault data of Choke adaptor in Houma Railway Service Section was used as an example for verification. The results show that the WPA-BPNN fault diagnosis model simplifies the network structure compared to the traditional methods, shortens the training time, improves the fault diagnosis accuracy, and ensures train safety and efficient operation of the line.

choke adaptor; fault diagnosis; rough sets; wolf pack algorithm; neural network

10.19713/j.cnki.43−1423/u.2019.04.030

U224.2

A

1672 − 7029(2019)04 − 1067 − 07

2018−05−18

国家自然科学基金资助项目(61763023)

郑云水(1972−)，男，甘肃定西人，副教授，从事交通信息与工程研究；E−mail：1094006476@qq.com

(编辑 蒋学东)