Levy型劲性支撑穹顶自振特性试验

孙国军，李晓辉，薛素铎，任竞赢



Levy型劲性支撑穹顶自振特性试验

孙国军，李晓辉，薛素铎，任竞赢

(北京工业大学建筑工程学院，北京 100124)

劲性支撑穹顶结构是近年来在索穹顶结构的基础上提出来的一种新型结构体系，它把索穹顶结构下部的拉索全部用高强钢拉杆代替，既保留了索穹顶结构造型美观、构造轻盈等优点，同时又解决了柔性索穹顶在张拉成形过程中杆件定位难且由于无预应力而导致的无整体刚度的问题．为研究Levy型劲性支撑穹顶结构的自振特性，本文设计了一个6m跨度的Levy型劲性支撑穹顶结构，并在试验场地张拉成型，同时测得实际内力与设计内力误差基本在1%以内．以这个试验模型为研究对象，采用激振器正弦激励法测定了该结构在初始预应力、满跨荷载以及半跨荷载3种荷载状态下的自振特性，得到了该结构在不同荷载状态下自振特性的变化规律．结果表明：该Levy型劲性支撑穹顶自振频率均较为密集，与索穹顶结构相似，验证了劲性支撑穹顶结构张拉成型的可能性与体系的合理性；不同状态下该Levy型劲性支撑穹顶自振频率理论值与试验值误差较小，均在±6%以内；在全跨荷载和半跨荷载分别作用下，低阶频率随荷载增加而增大，高阶频率随荷载增加反而有一定的降低趋势；该Levy型劲性支撑穹顶结构阻尼比基本在0.0081～0.0132之间，建议具有与该Levy型劲性支撑穹顶试验模型相似结构形式的Levy型劲性支撑穹顶在实际动力响应分析过程中阻尼比取0.01．

Levy型劲性支撑穹顶；自振特性；自振频率；阻尼比

近年来，大跨度空间结构得到了长足的发展，新型结构形式不断涌现．劲性支撑穹顶结构是北京工业大学薛素铎教授提出的一种新型的大跨度预应力空间结构，该结构上部是预应力空间索网体系，下部用高强钢拉杆代替了索穹顶结构中原有的柔性拉索，使之下部构件自身具备了一定的抗弯刚度．这种结构形式主要解决了索穹顶在施工成形过程中柔性构件定位困难的问题[1]．这种新型张拉整体的空间结构形式，其自振特性是整体结构进行抗震和抗风分析的基础．结构自振特性通常是经有限元软件计算分析得到，但这种方法尚不能准确表达结构真实的模态性能，为此需通过模型试验进行更为系统的研究[2]．

目前，对一些带拉索构件的预应力空间结构自振特性的研究已经取得了一定成果．陈志华等[3]分别采用脉动激励和锤击激励两种不同激励作用，对直径为18.5m的弦支穹顶结构进行了自振特性试验研究；张爱林等[4]考虑不同施工阶段，对北工大体育馆弦支穹顶结构1∶10模型进行了自振特性测定试验研究；张晓燕[5]针对Levy型索穹顶结构的自振特性进行了参数分析，探讨了结构几何参数变化对自振频率和振型的影响；王振华[6]对Levy型索穹顶结构在不同预应力情况下的自振特性进行了研究．

本文采用正弦激励法[7]对跨度为6m的Levy型劲性支撑穹顶结构模型进行模态试验研究，主要考虑预应力初始态、全跨荷载作用、半跨荷载作用3种不同情况，分析自振特性的变化规律，确定在抗震或者抗风分析设计过程中阻尼比适宜的取值范围．

1 试验模型

1.1 模型设计

该Levy型劲性支撑穹顶结构试验模型由40根脊索、40根斜杆、17 根撑杆、16根环杆组成，下层共2圈环向拉力构件．其中，脊索采用直径8.8mm的钢拉索，斜杆和环杆都采用直径8.8mm的钢拉杆，共有50个节点．该结构为中心对称结构，最外圈索杆与直径为6m的环梁相连，试验模型示意和实物照片分别如图1和图2所示．

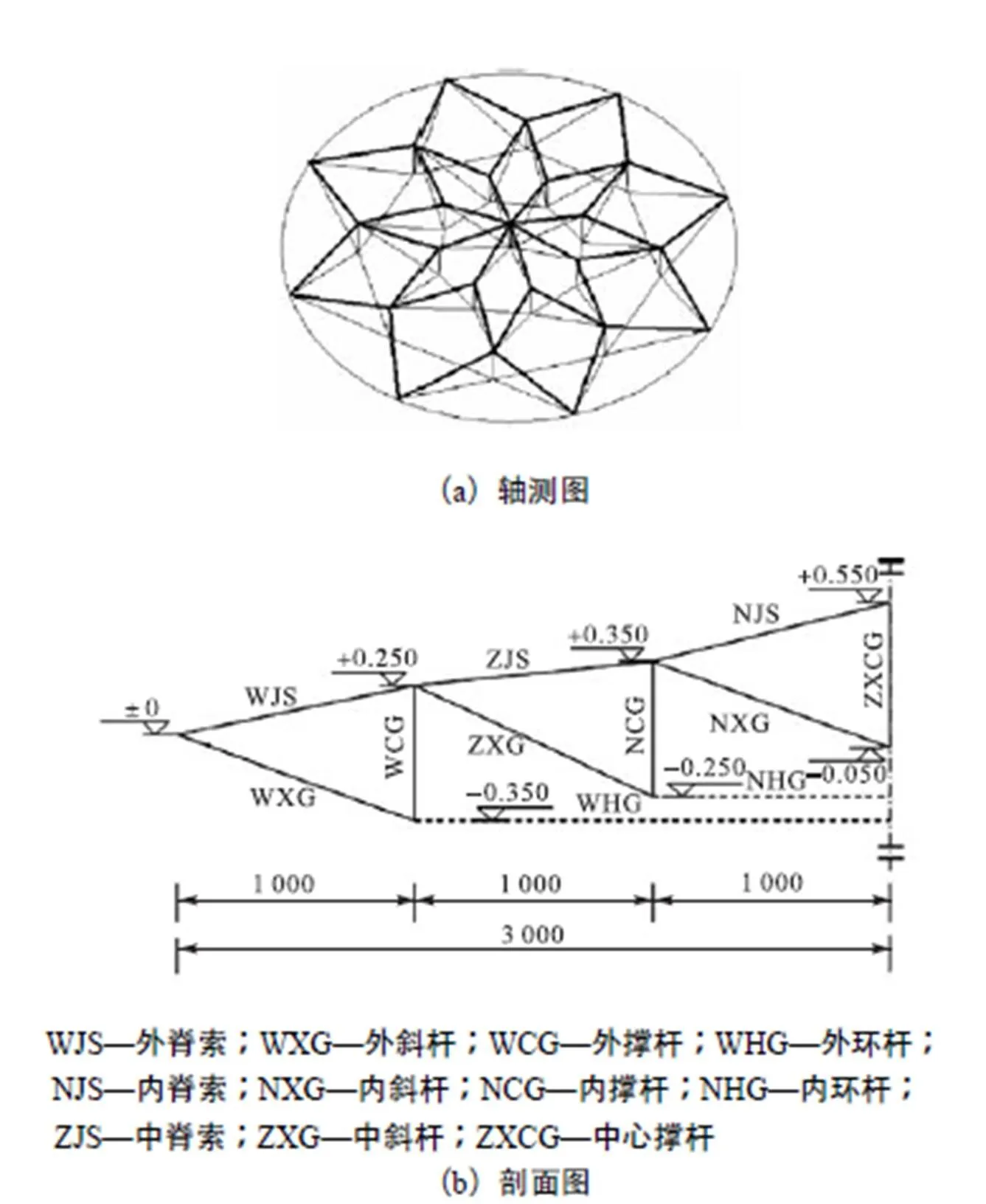
图1 试验模型示意

图2 试验模型照片

1.2 构件设计

该Levy型劲性支撑穹顶结构各构件截面尺寸信息见表1．鉴于试验所用钢拉杆和钢拉索的材料力学性能未知，采用抽样方法在北京工业大学强度检测所对两种构件的力学性能进行了标定．最终测得钢拉杆和钢拉索的弹性模量、实测破断力以及等效截面积在表2中列出．

表1 试验构件截面尺寸

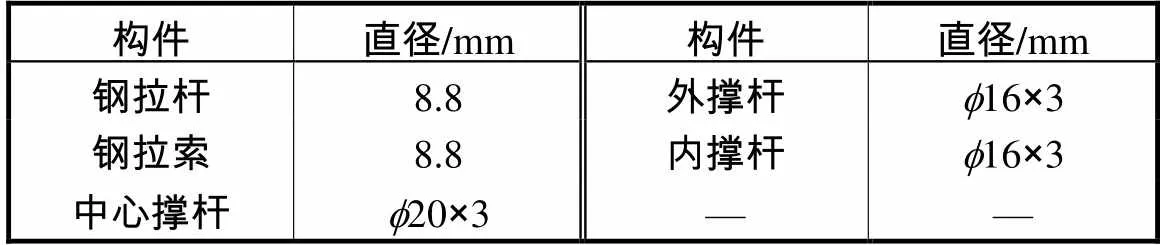
Tab.1 Section size of test member

表2 钢拉索及钢拉杆弹性模量、破断力及等效截面积实测值

Tab.2 Measured values of elastic modulus, breaking load and equivalent cross-sectional area of steel rod and cable

1.3 预应力设计

试验开展前，根据预设节点坐标，调整拉索端部调节螺杆的长度对拉索施加预拉力，在索头和拉杆上贴置应变片测定拉索和拉杆中的实际内力，同时在环索布置拉力传感器对索力进行校核，以保证数据的可靠性．结构初步张拉成型后，参考成型态各节点坐标，对各构件的内力进行多次微调，直至其与设计值基本一致，各构件实测内力值与理论内力值见表3．

表3 劲性支撑穹顶各构件初始内力理论值与实测值

Tab.3 Theoreticalforce and measured force of the rigid bracing dome

2 自振特性试验设计

2.1 测点布置

该Levy型劲性支撑穹顶结构径向单元为联方型，结构本身仍具有较好的平面外稳定性和抗扭刚度．同时，在实际工程中，劲性支撑穹顶结构成型后，上面一般会铺设柔性张力屋面或者刚性屋面，会增加结构的整体稳定性，从而在一定程度上避免了结构出现扭转变形．故试验过程中只采集结构的竖向加速度信号，振动测点选取16个点布置向振动传感器，如图3所示．向振动传感器布置在撑杆上节点部位．考虑到外部激励可能对试验造成的影响，本试验中分别在两个不同激振点处施加激励，最终取两组试验值的平均值作为该结构的实际结果[8]，激振点位置如图4所示．

图3 Z向振动传感器布置

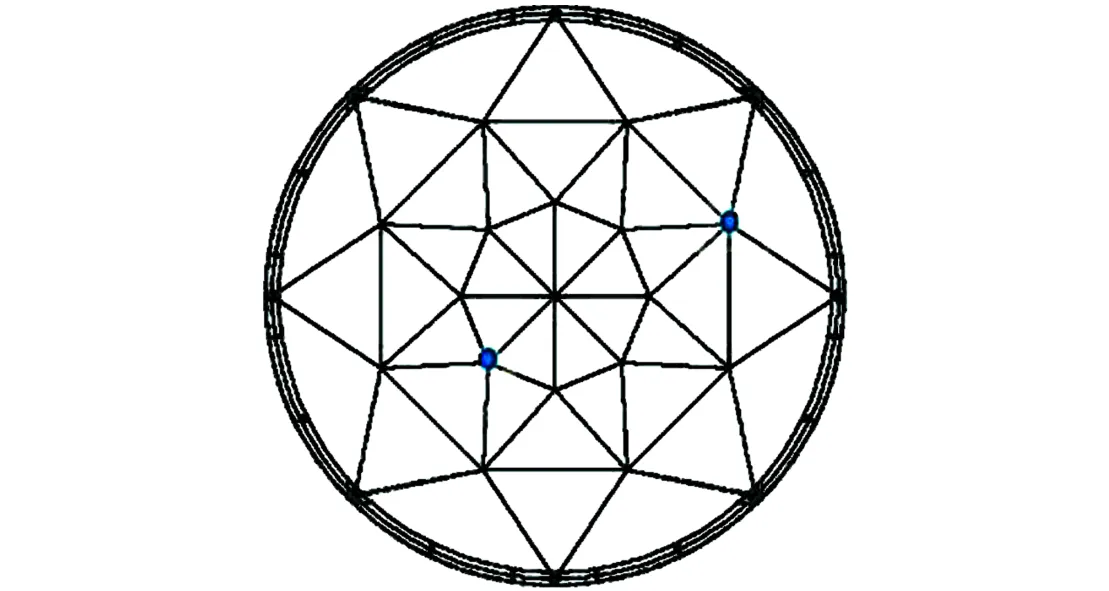
图4 激振点分布

2.2 试验原理

试验方案选正弦激励法，利用正弦激振器对试验模型上的激振点施加正弦激振荷载，促使Levy劲性支撑穹顶结构试验模型整体产生振动[3]，由CBook2000系列加速度数据采集系统获得布置在试验模型各节点上的传感器所产生的信号，然后通过MATLAB进行分析计算各个测点的响应数据，得出Levy劲性支撑穹顶结构试验模型的自振频率．通过互谱计算分析得到Levy劲性支撑穹顶结构试验模型中不同节点位置处的加速度传感器共振曲线相位关系，进而分析出不同频率的相应振型．根据黏滞阻尼理论以及试验获得的衰减曲线，计算Levy劲性支撑穹顶结构试验模型的阻尼比[9]．

阻尼比按如下公式进行计算

   (1)

式中：为阻尼比；y和y＋1表示相隔一周的振动幅值；和分别表示无阻尼和有阻尼振动频率．

令为振幅的对数衰减率，

   (2)

则式(1)变成

   (3)

当＜0.2时，式(3)可简化成

(4)

为减小外部环境激励可能对模态试验造成的影响，试验中分别对两个激振点各进行10次激励过程，将10次试验结果的平均值作为最终试验值．

2.3 试验方案

在不同荷载作用下的劲性支撑穹顶与仅在预应力态下相比，不仅仅改变了上部结构的自重，也改变了预应力态的分布，这两者的变化都会改变整体结构的自振频率与阻尼等特性，且这些是整体结构抗震或抗风性能分析的主要参数．为了充分测定荷载对结构模态特性的影响程度，本文分别考虑了全跨荷载与半跨荷载两种荷载形式，即本试验分别测试初始预应力状态、满跨静荷载和半跨静荷载3种工况下Levy型劲性支撑穹顶结构的动力特性．

3 试验过程及结果

3.1 初始模态试验

本试验采用正弦激励的方法，首先采用激振器在激振点位置上进行一次快速变频激振试验，初步确定可能出现共振峰值的频率范围；然后通过激振器调整到不同频率，在激振点位置对Levy劲性支撑穹顶结构试验模型进行强迫振动，获得稳态振动下的频率输入与输出振幅．在放大系数接近峰值后，减小模型试验激振频率的变化间隔，获得较为准确的试验模型的共振曲线[9]；最后经过相应的计算分析处理，获得Levy劲性支撑穹顶结构试验模型的频率、振型和阻尼比．

从试验结果可以发现，该Levy型劲性支撑穹顶的各阶振型之间存在不同程度的变形耦合现象．由于结构的中心对称性，相邻阶振型之间的差别可能并不明显，这使得要准确识别出结构各阶振型的难度有所增加，加之试验环境和设备对振动信号采集也会产生一定的影响，故对试验模型进行动力测试时，并不能保证结构前几阶频率和振型被激发出来[10]．因此，本文将试验测得的振型图与理论分析获得的振型图进行对比分析，以确定各阶模态频率所对应的模态 阶数．

取各组试验对应前8阶模态重新编号，该Levy型劲性支撑穹顶结构部分试验频率值和理论频率值见表4，结构实测阻尼比见表5．在预应力初始态下时，该Levy型劲性支撑穹顶结构自振频率的试验值与理论值误差基本在5%以内；劲性支撑穹顶结构自振频率较为密集，与索穹顶结构相似，验证了劲性支撑穹顶结构张拉成型的可能性与体系的合理性. Levy型劲性支撑穹顶结构在预应力初始态时阻尼比在0.0081～0.0132之间．

表4 劲性支撑穹顶自振频率试验值与理论值

Tab.4 Test and theoretical values of self-vibration fre-quency of the rigid bracing dome

表5 劲性支撑穹顶试验模型实测阻尼比

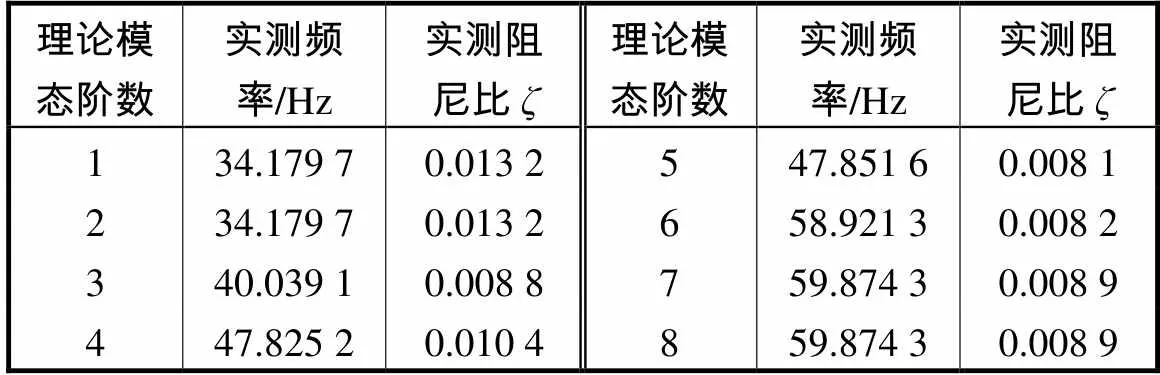
Tab.5 Measured damping ratio of the rigid bracing dome test model

3.2 全跨加载模态试验

试验中，荷载的加载方式采用挂沙袋法，将荷载加载于撑杆上节点，加载荷载值见表6，加载位置见图5(a)．荷载施加完成后需静置10min，以保证结构能够在荷载作用下进行充分的应力重分布．在图3所示位置布置加速度传感器来测得测点的加速度值，通过分析计算求得两者结构的自振频率与阻尼  比[11]，将两者结构的自振频率试验值与理论值列于表7，将其实测阻尼比列于表8．

表6 加载荷载值

Tab.6 Load values for loading

由对比可以得到如下结论：全跨荷载下，Levy型劲性支撑穹顶结构自振频率试验值与理论值误差不大，基本在5%以内；低阶自振频率随荷载增大而增大，且高阶频率有一定的减小趋势；Levy型劲性支撑穹顶在全跨荷载作用下，阻尼比在0.0084～0.0128之间．

图5 加载位置

表7 全跨荷载下劲性支撑穹顶自振频率试验值与理论值

Tab.7 Test and theoretical values of self-vibration fre-quency of the rigid bracing dome under full-span load

表8 全跨荷载下劲性支撑穹顶试验模型实测阻尼比

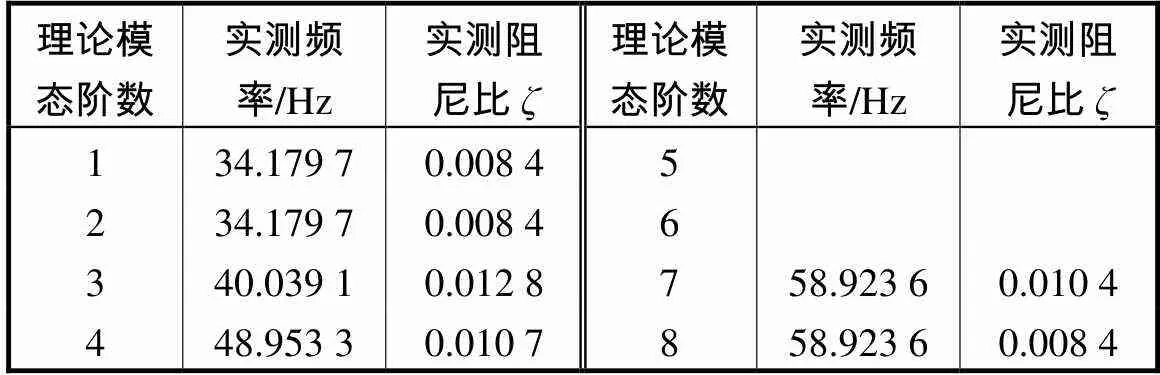
Tab.8 Measured damping ratio of the rigid bracing dome test model under full-span load

3.3 半跨加载模态试验

对Levy型劲性支撑穹顶按照图5(b)所示的加载位置施加半跨荷载，荷载大小见表6．在图3所示位置布置加速度传感器来测量测点的加速度值，通过分析计算求得两者结构的自振频率与阻尼比，将结构的自振频率试验值与理论值列于表9，将其实测阻尼比列于表10．

由对比可知，半跨荷载下Levy型劲性支撑穹顶结构自振频率的试验值与理论值误差基本在5%以内．劲性支撑穹顶低阶自振频率较预应力态有所增大，高阶自振频率较预应力态有所减小．说明半跨荷载作用改变了结构的各刚度分布，同时表明外荷载的作用并不完全等效于结构质量的增加，其对结构刚度也有一定的影响．Levy型劲性支撑穹顶在半跨荷载作用下，阻尼比在0.0088～0.0120之间．

表9 半跨荷载下劲性支撑穹顶自振频率试验值与理论值

Tab.9 Test and theoretical values of self-vibration fre-quency of the rigid bracing dome under half-span load

表10 半跨荷载下劲性支撑穹顶试验模型实测阻尼比

Tab.10 Measured damping ratio of the rigid bracing dome test model under half-span load

4 结 论

本文采用激振器正弦激励法完成了跨度为6m的Levy型劲性支撑穹顶结构模态特性试验，将试验结果与理论模拟分析结果进行对比，得出如下结论：

(1)该Levy型劲性支撑穹顶结构在3种不同荷载状态下的自振频率均较为密集，与索穹顶结构相似，验证了劲性支撑穹顶结构张拉成型的可能性与体系的合理性；不同状态下该Levy型劲性支撑穹顶自振频率理论值与试验值误差较小，均在±6%以内；

(2) 全跨荷载和半跨荷载作用下，低阶频率随荷载增加而增大，高阶频率随荷载增加而有一定的降低趋势；

(3) 该Levy型劲性支撑穹顶结构阻尼比基本在0.0081～0.0132之间，建议具有与该Levy型劲性支撑穹顶试验模型相似结构形式的Levy型劲性支撑穹顶在实际动力响应分析过程中阻尼比取0.01．

［1］ 薛素铎，高占远，李雄彦，等. 一种新型预应力空间结构：劲性支撑穹顶[J]. 空间结构，2013，19(1)：1-7.

Xue Suduo，Gao Zhanyuan，Li Xiongyan. A new prestressed spatial structure：Rigid bracing dome[J]. Space Structures，2013，19(1)：1-7(in Chinese).

［2］ 薛素铎，何永发，李雄彦，等. 劲性支撑穹顶结构模态性能参数分析[J]. 世界地震工程，2015，31(1)：1-7.

Xue Suduo，He Yongfa，Li Xiongyan，et al. Modal characteristics parameter analysis of rigid bracing dome [J]. World Seismic Engineering，2015，31(1)：1-7(in Chinese).

［3］ 陈志华，郭 云，李 阳. 弦支穹顶结构预应力及动力性能理论与实验研究[J]. 建筑结构，2004，34(5)：42-45.

Chen Zhihua，Guo Yun，Li Yang. Theoretical and experimental study on the prestress and dynamic performance of a string-supported dome[J]. Building Structure，2004，34(5)：42-45(in Chinese).

［4］ 张爱林，王冬梅，刘学春，等. 2008奥运会羽毛球馆弦支穹顶结构模型动力特性试验及理论分析[J]. 建筑结构学报，2007，28(6)：68-75.

Zhang Ailin，Wang Dongmei，Liu Xuechun，et al. Dynamic performance experiment and theoretical analysis on the suspend-dome structure model of the badminton gymnasium for 2008 Olympic Games[J]. Journal of Building Structure，2007，28(6)：68-75(in Chinese).

［5］ 张晓燕. 索穹顶结构的静自振特性研究[D]. 北京：清华大学土木水利学院，2004.

Zhang Xiaoyan. Static and Dynamic Analysis of the Cable Dome[D]. Beijing：School of Civil Engineering，Tsinghua University，2004(in Chinese).

［6］ 王振华. 索穹顶与单层网壳组合的新型空间结构理论分析与试验研究[D]. 杭州：浙江大学建筑工程学院，2009.

Wang Zhenhua. Theoretical and Experimental Research on a New Spatial Structure Composed of Cable Dome and Singlee-Layer Lattice Shell[D]. Hangzhou：College of Civil Engineering and Architecture，Zhejiang University，2009(in Chinese).

［7］ 何永发，薛素铎，李雄彦，等. 肋环形劲性支撑穹顶结构动力特性分析[C]//第15届空间结构学术会议论文集. 上海，中国，2014：181-186.

He Yongfa，Xue Suduo，Li Xiongyan，et al. Analysis of dynamic characteristics of ribbed elastic support dome structure[C]//Proceedings of the 15th Academic Conference on Space Structure. Shanghai，China，2014：181-186(in Chinese).

［8］ 包红泽. 鸟巢型索穹顶结构的理论分析与试验研究[D]. 杭州：浙江大学建筑工程学院，2007.

Bao Hongze. The Theoretical and Experimental Research of Biro-Nest Cable Dome[D]. Hangzhou：College of Civil Engineering and Architecture，Zhejiang Univer-sity，2007(in Chinese).

［9］ 刘晶波，杜修力. 结构动力学[M]. 北京：机械工业出版社，2005.

Liu Jingbo，Du Xiuli. Structural Dynamics[M]. Beijing：China Machine Press，2005(in Chinese).

［10］ 李可娜，殷志祥. Kiewitt型弦支穹顶结构自振特性研究[J]. 空间结构，2011，17(1)：21-26.

Li Kena，Yin Zhixiang. Natural vibration characteristic of Kiewitt suspendome[J]. Spatial Structure，2011，17(1)：21-26(in Chinese).

［11］ 刘 伟，高维成. 单层短程线网壳结构模型试验研究[J]. 实验力学，2006，21(4)：519-526.

Liu Wei，Gao Weicheng. Experimental study on the model of single-layer short-range reticulated shell structure[J]. Journal of Experimental Mechanics，2006，21(4)：519-526(in Chinese).

Experiment on Self-Vibration Characteristics of Levy-Type Rigid Bracing Dome

Sun Guojun，Li Xiaohui，Xue Suduo，Ren Jingying

(College of Architecture and Civil Engineering，Beijing University of Technology，Beijing 100124，China)

The rigid bracing dome is a new type of structural system proposed based on the cable dome in recent years. It replaces the cables in the lower part of the cable dome with high-strength steel tie rods，which not only retains the advantages of attractive appearance and lightness of the cable dome，but also overcomes the difficulty of bar positioning in the process of cable dome construction and forming. The problem that the structure has no integral stiffness due to no prestress of the bar is also solved. To investigate the self-vibration characteristics of the Levy-type rigid bracing dome，a Levy-type rigid bracing dome with a 6m span was designed and stretched and formed at the test site. The error is within 1% between the measured actual internal force and the designed internal force. Taking this experimental model as the research object，the self-vibration characteristics at three kinds of load conditions(the initial pre-stress，full-span load and half-span load of structure) were measured by the sinusoidal excitation method. The variation of the self-vibration characteristics of the structure under different load conditions was obtained. Results indicate that the self-vibration frequency of the Levy-type rigid bracing dome was relatively dense，which is similar to the cable dome. This proves that the structural form is reasonable and can be formed by means of tensioning. The difference between the theoretical value of the Levy-type rigid bracing dome and the experimental value was within ±6% under different conditions. Under the condition of full-span load and half-span load respectively，the low-order frequency increases with the increase in the load，and the higher-order frequency decreases with the increase in the load. The damping ratio of the Levy-type rigid bracing dome was basically between 0.0081 and 0.0132. The recommended damping ratio should be 0.01 in the actual dynamic response analysis process when a structure has a similar structural form to the Levy-type rigid bracing dome test model.

Levy-type rigid bracing dome；self-vibration characteristics；self-vibration frequency；damping ratio

10.11784/tdxbz201811031

TU394

A

0493-2137(2019)07-0719-06

2018-11-12；

2019-01-10.

孙国军（1984—  ），男，博士，讲师.

孙国军，sunny2369@163.com.

国家自然科学基金资助项目(51878013)；国家自然科学基金青年基金资助项目(51408016).

the National Natural Science Foundation of China(No.51878013)，the National Natural Science Foundation Youth Fund Project(No.51408016).

(责任编辑：樊素英)