老年人中医药服务健康效用的赛斯通量表度量

张天懿

(天津中医药大学管理学院，天津 301617)

中医药服务和健康方面，许多客观的措施用于监测患者健康结果或评估健康干预，但也有主观的措施。对于后者，很难获得度量数据，这些数据需要量化健康结果，如功能障碍、副作用的严重程度和健康状况等。本研究利用赛斯通量表和模型对京津地区的老年人进行了实证分析，重点研究了健康状态的价值。

1 资料与方法

1.1资料来源 通过天津中医药大学第一附属医院和天津中医药大学附属保康医院门诊患者和北京昌平区回龙观地区中医门诊患者(65～85岁，男412例，女409例)共计822份问卷调查。

1.2研究方法 中医药服务健康主观度量的核心活动是数据产生的信息。扩展模型包括简单和直接的问卷，只要提供了足够的信息以达到定量的度量，这些任务很容易执行。基本上，人们有2个判断的标准。更简单的方法是一组实体，例如，健康状态。另一种基于成对比较的方法，要求受访者从中选择自己喜欢的状态。对备选方案进行成对比较通常是可行的。如果呈现的实体很难区分，或者度量的维度不容易理解，可以进行缩放，变换模型和进行联合分析。其中最基本的是赛斯通模型。

赛斯通提出了“比较判断法则”，并讨论其潜力和局限性。选择是由“甄别过程”来调节的。赛斯通将此定义为生物体识别、区分或对刺激做出反应的过程。考虑任意两个健康状态i和j的判别过程的理论分布，在比较判断法则(LCJ)模型中，与给定的健康状态相关联的分布的标准偏差称为该健康状态的判别离散度〔1〕。不同的健康状态可能不同。让μi和μj对应于两个健康状态的刻度值。区别(μi-μj)是用μij写的，用区别性的单位来度量。完整形式LCJ如方程①：j表示之间的相关性辨别过程i和j，Zij是单位正常偏离理论对应比例的时候，健康状态j判断大于健康状态。

①

在赛斯通缩放的标准方法中，成对比较方法用于收集响应数据。根据该法则，老人被迫表达对一种状态的偏爱。所有可能的配对都通过配对比较来评估。这与理论上的推导是一致的。另一种响应模式是秩和检验数据，它也能够生成适合赛斯通缩放的数据，赛斯通量表的LCJ定义了这类模型。

2 结 果

2.1原始数据分析 在n(n-1)/2对健康状态已经满足前提假定条件下，原始数据的每一个健康状态的次数被其他健康状态所选择。这些观察到的频率可以放在方阵f中。第k行和第l列中出现的一般元素fij表示观察到的健康状态的次数，比健康状态j更好或更差。矩阵P是由矩阵f构成的，元素Pij是健康状态i在健康状态j中被观察到的比例。矩阵P用于构造矩阵Z，即基本的变换矩阵。元素Zij是与元素Pij相对应的正常单位偏差。元素Zij对所有Pij值小于0.5的值都是正的。在对角线上输入0；因为我们通常可以假设μi-μj=0。将量表值作为列总数的平均值，用Z矩阵的所有非缺失元素进行计算。

数据来自于2017年北京回龙观地区和天津南开区万兴街的EuroQol(EQ)-5D估值研究。EQ-5D分类根据5个属性描述健康状况：流动性、自理、日常活动、疼痛/不适、焦虑/抑郁〔2〕。每个属性有3个级别。健康状态描述是通过为每个属性取1级而构建的。EQ-5D属性和水平允许243种不同的健康状态描述，研究可以分成几个部分的面对面访谈〔3〕。受访者填写带有社会经济和背景问题的调查问卷后，用标准的EQ-5D描述自己的健康状况。然后，他们将健康状态列在卡片上，然后把卡片放在EQ-5D视觉模拟量表上。最后用健康经济学中常见的估值技术视觉模拟评分法(VAS)即时间权衡法进行评估。

在对原始数据进行了模拟之后，选取了17个健康状态，以“11111”和“死亡”作为补充。数据输入赛斯通量表中。被调查者将19张卡片放在1个EQ VAS上，健康状态的位置之间的间隔与他们感知到的差异相对应，标准的20 cm EQ VAS通常被称为EQ温度计。它的端点是100，最好的健康状态是100，最差的是0。

2.2健康状态的分析评价 分析LCJ适用于大多数的研究情况。不管刺激物的数量如何，通常有更多的未知参数，而不是观测方程。两个前提假设是老年人们正在考虑他们喜欢的每个健康状况，和假设每个状态可能显示相同的变化。

用1个基本的数学方程，奇异值分解(SVD)来测试VAS数据的单维性。SVD与因子分析(FA)密切相关。SVD方程与FA的主要区别在于后种方法是基于相关性或协方差分析，而SVD是基于对原始数据的分析。数据的原始度量结构(范围、方法)不会被SVD改变，因此该技术可将原始数据分解为其主要特性。与因子分析一样，SVD也试图识别潜在的维度或因素。在计算Z矩阵列的均值后，进行转换，以达到与健康状态“11111”在1.0和“死亡”为0.0时的比例。这是健康经济学的基本要求。用SPSS19.0计算描述性统计和SVD分析及赛斯通缩放计算(矩阵模块)。

表1给出了所有健康状态的平均值和标准误，并给出了排名和VAS数据的“死亡”。1个健康状态(“11131”)的平均秩值为8.77，与平均VAS值不相同。这可能是由于这个状态的VAS值的1个非正态分布。VAS中没有观察到这种不一致。在极端状态下，平均VAS值和平均秩的标准误更小。这是1个常见的可解释的特性。SVD分析支持原始VAS数据的单维性，94%的方差由1个维度解释。平均秩和均值VAS值之间存在明显的逆线性关系，在平均VAS值之间找到了类似的关系，在平均等级和得到的赛斯通值之间也发现了类似的关联性。

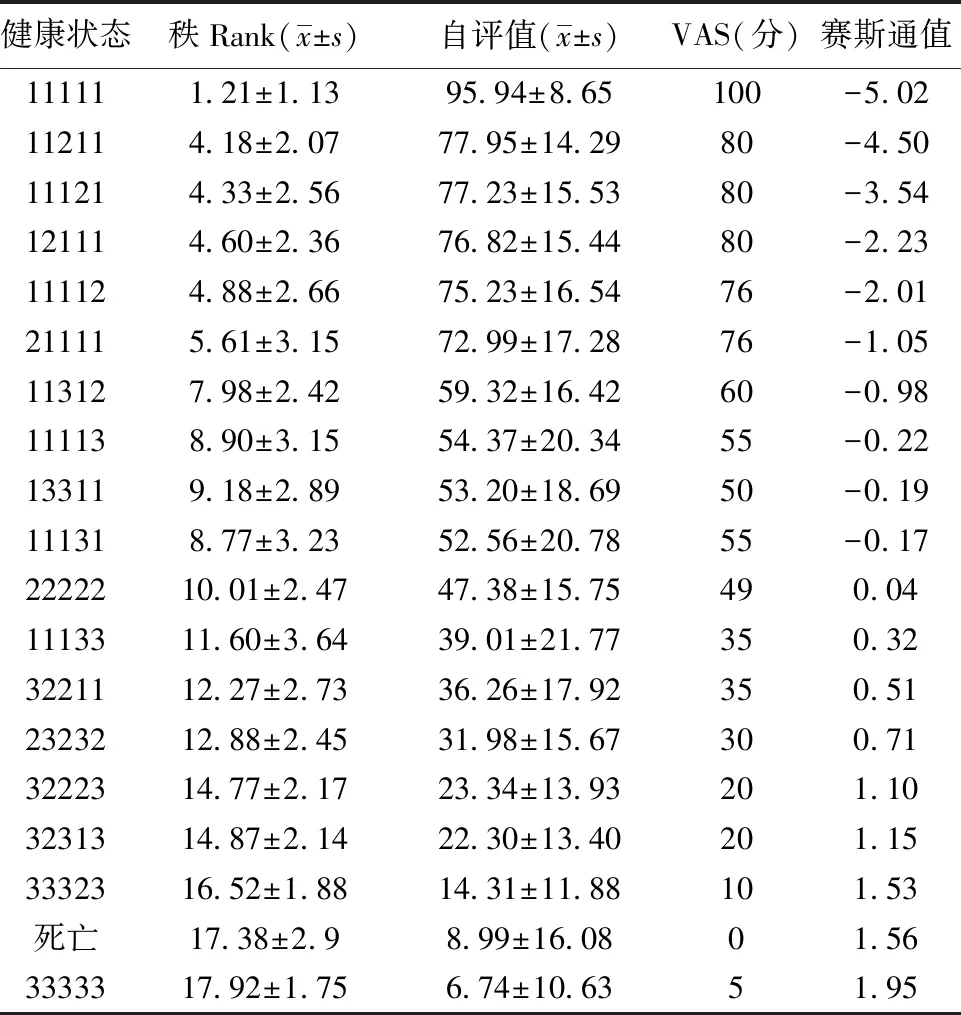
表1 健康状态赛斯通的缩放结果与VAS值比较(n=822)

3 讨 论

3.1中医药服务相关健康测量分析 样本患者年龄从65～85岁，看中医和保健康复的居多。一般来说，中等状态群的赛斯通值略低于VAS值。在VAS和赛斯通规模上，京津两个地区的位置几乎相同。特别是“死亡”和“11111”是VAS和赛斯通同规模的，因此定义上是相同的。与VAS值相比，在赛斯通量表中，中间状态的比例有所不同。鉴于课题经费和样本限制，研究结论有待进一步探讨。

研究利用中医药服务中健康相关数据，说明了赛斯通模型的潜力，可以推导出主观健康结果的度量值，对赛斯通模型的各种计算步骤进行了解释。在这种情况下，主观的健康结果由一组健康状态的描述组成，这些描述受到模型的计算步骤的影响。由于VAS也由相同的受访者执行，因此可以检查平均VAS值与派生的赛斯通值之间的一致性。研究发现，赛斯通模型产生的值与VAS值非常相似。在健康状态评估的背景下，尽管VAS是1个基于不同判断任务的更有认知要求的过程，但是在总体水平上，VAS和赛斯通的量表产生的结果几乎相同。因此，多项目VAS可能被认为是多重成对比较的复合分析，具有一定的等级。在平均等级和得到的赛斯通值之间也有相似之处。3种不同判断的基本信息过程可能非常相似。然而，赛斯通的缩放比VAS有优势，前者可以消除在VAS中可能发生的任何偏差。在VAS和赛斯通量表之间，并不意味着两种方法都能产生有效的健康状态值。需要更详细的实验研究才能得出这样的结论。

3.2应用建议 赛斯通模型的另一个局限性是基于正态分布，而Rasch模型和其他项目响应模型是基于Logistic函数，它具有计算和理论上的优点。赛斯通缩放的一个相关限制是，它假定但没有提供规模的单一维度的直接证据。在本研究中，通过对VAS数据的SVD分析，间接支持了赛斯通量表的单维性。

简单的数据收集方法在赛斯通模型下，有几个优点。这包括对老年人易于理解和管理及由于减少测量误差而提高可靠性。尤其是在受教育程度和计算能力有限的环境中，一项普通的测量策略可能在更广泛应用的技术上具有相当大的实际优势，对中医药健康服务的发展能够提供一定的支持。