六自由度机械臂轨迹规划算法研究

2019-04-25任伟，江明

安徽工程大学学报 2019年6期

任伟，江明

(安徽工程大学电气工程学院，安徽芜湖 241000)

无论是结构型机器人(机械臂)，还是移动型机器人，想要实现其连续平稳地运行，对于其轨迹的提前规划都不容忽视。近年来，很多工业制造行业中已经大量投入使用工业应用型机械臂。由于应用场景和应用目的不同，使得轨迹规划出现了多种算法。对于比较简单的点到点(PTP)操作，轨迹规划中更多的是使用一些简单的插值方法。文献[1-4]中针对机器人不同的应用场景，采用多项式、S曲线、3次B样条等插值算法，实现了机械臂的轨迹规划。而对于较为复杂目的的轨迹规划，通常采用的是基于分段插值的轨迹规划思想。针对工业机器人运行不平稳问题，文献[5]中采用3-3-3-3-3多项式算法，对搬运机器人实现轨迹规划，但仍存在中间过程较多、复杂度较高的问题。同样基于运行不平稳问题，为了改善算法复杂度，文献[6]中采用5-3-5多项式算法，实现了机械臂的关节角在关节空间的分段插值，完成码垛功能。而对于标准B样条插值算法存在启停位置振动问题，文献[7]中运用了高阶次多项式与B样条优化相结合的插值算法，很好地解决了这一问题。对于机器人在应用过程中出现的问题，还有很多学者进行了一系列的优化研究。

针对PUMA560机器人，分别从运动学建模和轨迹规划两个方面进行探究。首先，对于运动学建模问题，主要是利用D-H参数法和解析法构建其正逆向运动学模型。其次，对于轨迹规划问题，分析讨论了4-5-4多项式分段插值算法原理，并与传统的3-5-3多项式分段插值算法进行了对比研究。最终采用4-5-4多项式分段插值算法实现各关节角度插值，并利用正向运动学获得机器人末端的运行轨迹，实现了机器人平稳、连续运行。

1 运动学分析

机器人的运动学问题，指在不关注力和力矩的前提下，从机器人的几何结构角度去研究机器人在不同空间(关节、笛卡尔)下的运行状况。对于机器人运动学的研究，主要从正向和逆向两个方面进行研究分析，前者是指在已知连杆参数和关节相关变量(角度或位移)前提下，求解机器人末端的位姿；后者是指在已知连杆参数和末端位姿前提下，求解机器人所有的关节变量值[8]。

1.1 连杆关系

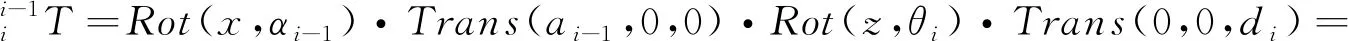
(1)

1.2 PUMA560机器人

PUMA560是一款通用六自由度关节型机器人，末端执行器位置是由前3个关节所决定，末端执行器方位是由腕部的3个关节所决定，其连杆结构图如图2所示。

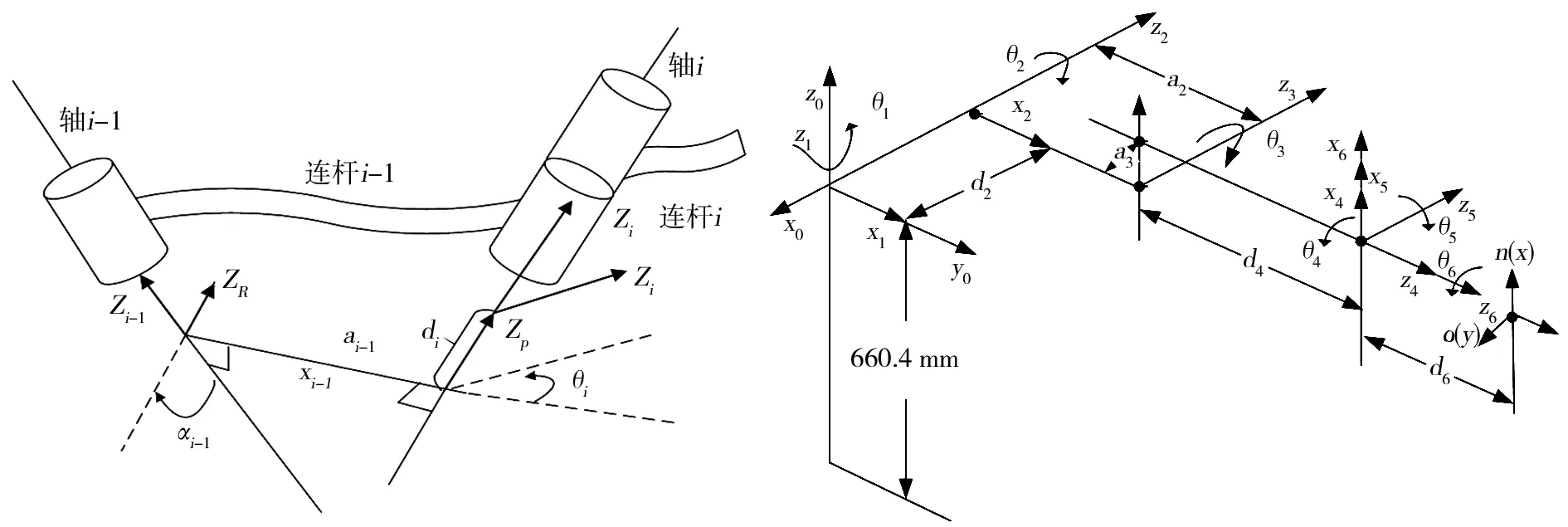
图1 连杆相邻坐标系变换图2 PUMA560连杆坐标系

PUMA560机器人具体的D-H参数变量以及关节角度运行变化范围如表1所示。由表1可知，相关变量参数d2=149.09 mm,d4=433.07 mm,d6=56.25 mm,a2=431.8 mm,a3=20.32 mm。

表1 PUMA560连杆参数

(2)

(3)

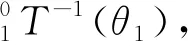
(4)

(5)

2 4-5-4多项式分段插值

机械臂在运行过程中一旦出现不平稳的问题，不仅会影响运行任务的完成，还会影响其本体使用寿命。此项研究设计的目的是使得PUMA560机器人能够在任务空间准确、平稳地完成搬运任务。传统的3-5-3多项式分段插值算法对机器人的启停位置无法很好地控制，且不能对关节角度运行变化的速度和加速度同时进行配置，可能会引起机器人出现运行不连续和不平稳的问题。因此提出一种4-5-4多项式分段插值算法，实现关节空间的各关节角度分段式轨迹规划。具体设计思想：

首先，在任务空间中确定起始点和终止点，并选取两个中间路径点。然后，根据逆向运动学，将任务空间轨迹关键点进行逆解，求出关节空间4组关键点的关节角度值。再利用分段思想，在关节空间中，分别对每个关节的角度变化进行三段式的4-5-4多项式插值规划，从而获得各关节的角度插值序列。最后利用运动学正解将各关节角度插值序列转化为末端位姿，从而获得末端运动轨迹。对4个关键点利用逆向运动学反解，可以得到各关节变量值，具体的空间位置点及其对应关节角度值如表2所示。

表2 空间点及相应关节角度

4-5-4多项式分段插值算法，具体是指对机器人的各关节角度插值运算，在起始点Q0与上升点Q1关节角度间，运用4次多项式进行插值；在上升点Q1与下降点Q2的关节角度间，运用5次多项式进行插值；在下降点Q2与终止点Q3关节角度间，运用4次多项式进行插值。

为了在关节空间实现机器人的4-5-4多项式分段插值，需要对各个关节分别进行三段式的多项式插值分析，设这三段目标轨迹的角度插值函数为[12]:

(6)

式中,qi1(t),qi2(t),qi3(t)为第i关节的第1,2,3段的关节角度插值函数;aijk为第i关节的第j段插值函数的第k项系数，i可取1,2,3,4,5,6;j可取1,2,3;k可取0,1,2,3,4,5。

对式(6)关于时间求导，获得相应关节的角速度以及角加速度插值函数，如式(7)所示。

(7)

为了实现机器人运行的连续性、平稳性和高效性，需要对各关节运行的三段轨迹进行约束：①三段轨迹的起点和末端点的关节角度必须与给定关键点位置保持一致。②各段轨迹起点的角速度、角加速度与前一段轨迹末端点的角速度、角加速度保持一致。③关节运行的第1段轨迹起点和第3段轨迹末端点的角速度和角加速度都为0。④确保整个过程规划的相应关节运行角度、速度和加速度变化保持连续。

对于3个插值区间运行时间的设定，当设定值较小时，会使得关节运行的角速度和角加速度变化过大；当设定值较大时，会增大计算数值，延长运行时间。为了便于算法计算研究，分别将3个插值区间的运行时间都分配为2s。根据上述约束条件以及式(6)、式(7)分析获得各关节在3个阶段角度插值函数求解系数的公式如式(8)、式(9)、式(10)所示。

在0～2 s，第一阶段求系数参数的公式为

(8)

在2～4 s，第二阶段求系数参数的公式为

(9)

在4～6 s，第三阶段求系数参数的公式为

(10)

3 仿真验证

3.1 运动学验证

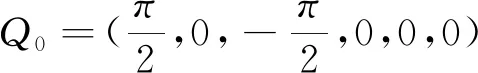
(11)

对于6轴机器人的正逆向运动学模型的验证，主要是借助Robotics Toolbox 9.10，正向求解是运用fkine( )函数，逆向求解是运用ikine( )函数[13],部分程序如下：

robot=SerialLink([L1,L2,L3,L4,L5,L6],'name','puma560');%建立机器人模型

Q0=[pi/2 0 -pi/2 0 0 0];%起始点角度值

T=robot.fkine(Q0);%利用正向运动学函数获得起始点位姿

Q1=robot.ikine(T);%利用逆向运动学函数获得各关节角度

Robot.plot(Q0);%获得机器人在Q0处位姿图

运行结果得到的末端位姿T矩阵与正向运动学推算的结果一致，而得到的Q1与Q0一致，证明了运动学模型的正确性。同样，也可以利用teach( )函数观察各关节角度与位姿的转换关系，仿真结果如图3所示，进一步验证所建机器人运动学模型的准确性。

3.2 任务空间仿真

PUMA560的各关节运行变化范围有限，使得机器人在运行过程中有限定的任务空间，所以使用蒙特卡洛法[14]对PUMA560任务空间进行分析，各关节角度通过式(12)进行计算。

Qi=Qimin+(Qimax-Qimin)*rand(N,1),

(12)

式中，Qi表示第i关节的角度值；Qimin,Qimax表示第i关节角度值的最小和最大值，i可取1,2,3,4,5,6;rand(N,1)随机产成N组(0,1)之间的随机数，N取30 000。

利用式(12)依次对6个关节角度变量取值，然后利用fkine( )函数求解出关节角度对应的任务空间点，MATLAB仿真得到的任务空间散点分布如图4所示[15],仿真得到的散点都是机器人在任务空间中可以到达的点。

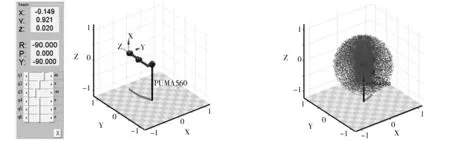
图3 PUMA560在(pi/2 0 -pi/2 0 0 0)处位姿图图4 PUMA560工作空间

3.3 轨迹规划仿真验证

针对PUMA560，基于相同数据和约束条件，分别利用4-5-4多项式分段插值和传统的3-5-3多项式分段插值算法进行轨迹规划，得到前3个关节角度、角速度和角加速度的插值结果如图5、图6、图7所示。由图5、图6、图7对比分析得出：

(1)两种不同算法在第2段(2～4 s)的关节变量控制上采用的都是5次多项式。通过对比分析，这两种算法在第2段控制所起的作用效果差不多。

(2)两种不同算法在第1段和第3段(0～2 s、4～6 s)的关节变量控制上，4-5-4多项式分段插值比3-5-3多项式分段插值算法控制得更好。在第1段和第3段关节变量控制上，如果采用3次多项式，它将无法对关节的角速度和角加速度同时进行配置，即第1段起始位置和第3段结束位置都无法准确同时控制角速度和角加速度为0，这可能会引起机器人振动，影响其正常运行。而利用4次多项式控制可以很好地弥补角速度和角加速度的同时配置问题，且4-5-4多项式分段插值算法控制的关节变量在相应时间段呈现的函数特性要比后者阶次更高，从图5、图6、图7中不难看出，在控制变量变化上呈现出平稳性和柔性更好的特点。

图5 axis1的角度、角速度、角加速度图6 axis2的角度、角速度、角加速度

图7 axis3的角度、角速度、角加速度

通过上面分析得出结论，在控制关节运行的相应变量方面，4-5-4多项式分段插值算法要比传统的3-5-3多项式分段插值算法更有优势。

根据表2中的数据，利用4-5-4多项式分段插值算法对各关节变量分别进行轨迹规划，得到的各关节角度、角速度以及角加速度插值结果如图8、图9、图10所示。得到的各关节变量变化都呈现出连续性和平稳性，且满足所要求的约束条件，仿真结果也进一步验证了4-5-4多项式分段插值算法的可行性。

对于4-5-4多项式分段插值得到的关节角度变化序列，利用运动学正解分析、计算和仿真得到PUMA560末端运行轨迹，机器人将在任务空间按规划轨迹依次通过各个位置序列点，具体如图11所示。

图8 各关节角度变化图9 各关节角速度变化

图10 各关节角加速度变化图11 PUMA560末端运行图

而对于机械臂在任务空间的稳定运行，最重要的就是控制其位置和速度的平稳连续变化。图12和图13分别是PUMA560末端在X/Y/Z 3个方向上的位置和速度变化图。通过分析可以清楚地观察到末端在X/Y/Z 3个方向上的位移、速度曲线都具有平滑连续等特性，能够满足PUMA560运行平稳条件，同时也进一步验证了4-5-4多项式分段插值算法的可行性、可靠性与准确性。