遗传算法在堆垛机路径优化上的应用研究
2019-04-25张新阳
张新阳,陈 玉,王 鹏
(安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
随着自动化生产技术的发展,企业在生产制造方面的竞争加大,产品的运输、检查及存储方面所占的比重越来越高。在产品的存储方面,自动化立体仓库的存储效率主要取决于堆垛机的运行速度、货位的优化存取[1]。有效解决货物在存取中效率低的问题,可以大大提高自动化立体仓库的工作效率。货架作为自动化立体仓库的存储部分,是仓储物流中一个重要环节[2],合理安排货位的出入库分配原则和分配策略,能有效降低搬运过程中的损耗,降低物流业务成本,提高物流行业收益。
1 自动化立体仓库模型设计
货位优化的目的是根据某一种货位分配原则,使得每一个货位能够合理且高效率地放入到合理的位置中。在自动化立体仓库中,货位的分配控制对象主要有3个,即堆垛机、货架和货架货位。通常自动化立体仓库主要由货架、堆垛机、运送工具以及控制台4个部分组成[3]。货架是货物存储的单元格整体;堆垛机是货物存储过程中的执行器;AGV小车或其他运送工具是货物输送桥梁;控制台是立体仓库的操作平台和观察平台。自动化立体仓库结构平面图如图1所示。
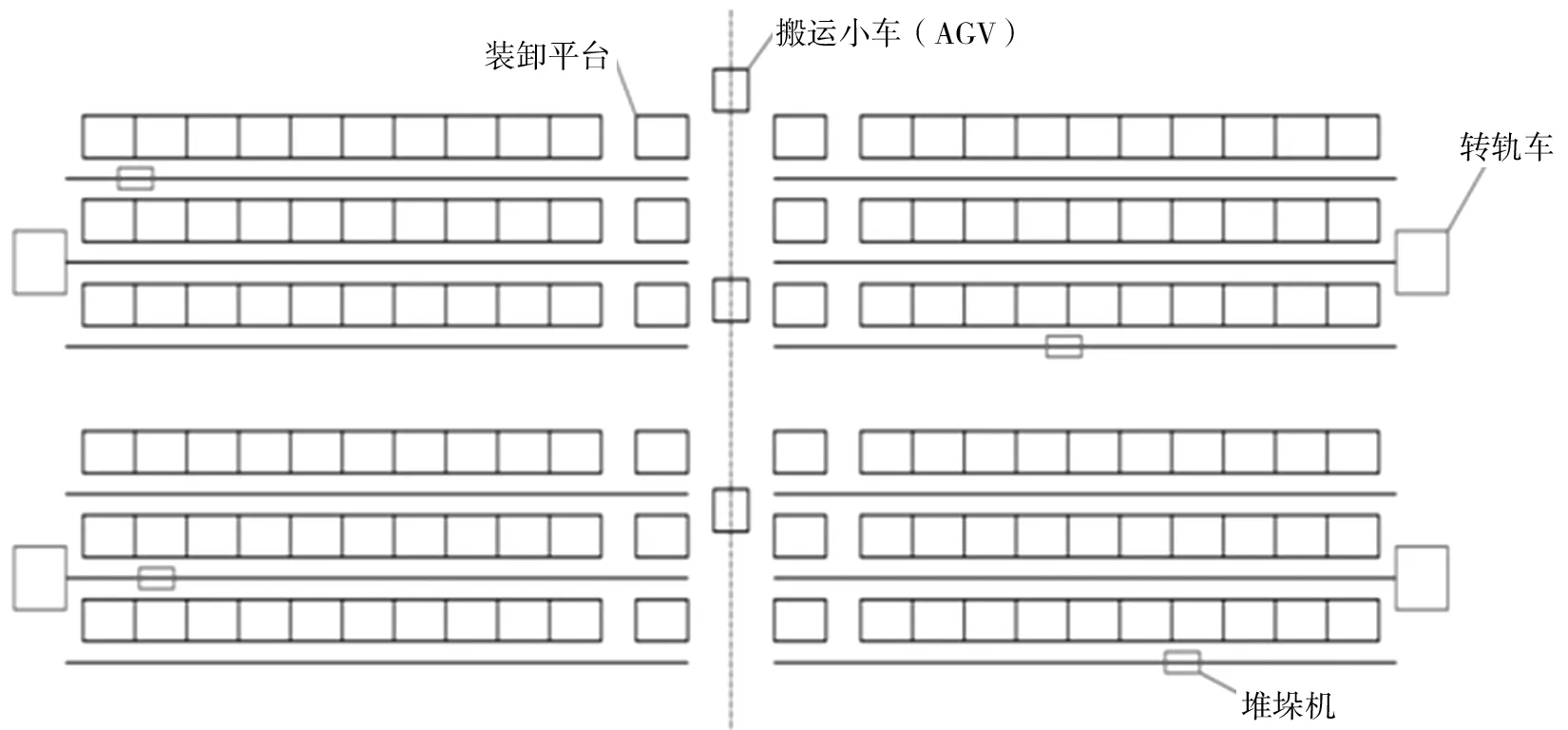
图1 自动化立体仓库结构平面图
立体仓库由计算机控制,先将立体的程序通过PLC输入计算机中,按照操作执行出库、入库等动作。当一批生产任务到达时,计算机按照指令顺序依次来执行出入库任务。由于出入库动作执行的顺序不一样[4],堆垛机路径也不同,因而堆垛机每次执行任务的时间也不同。
目前的自动化立体仓库存取的货物量较大,同时存在入库和出库同时进行的复合作业。复合作业要比单一作业的效率高很多。堆垛机存取路径如图2所示。对于复合作业,O为堆垛机周转平台,A点为储存货物点,B点为取出货物点,堆垛机所走的路径为O→A→B→O。假设自动化立体仓库每排共有m层n列,离地面最近的一层为第一层,离出入口最近的列为第一列。设O、A、B的坐标分别为O(0,0)、A(a,b)、B(c,d)。

图2 堆垛机存取路径
(1)对于货物复合作业,根据自动化立体仓库的出入效率原则,建立数学模型:
(1)
(2)
式中,f1(x,y)为每个托盘上货物的质量与其所在层的乘积之和;tij(x,y)为货物从O点出发执行相应任务后回到O点所需要的时间;vx为堆垛机水平运行速度;vy为堆垛机垂直运行速度;l为货格长;h为货格高;pij∈(0,1)为第i行j列的货物周转效率。
(2)根据货物上轻下重原则,由此可建立数学模型:
(3)
式中,Gij为货架第i行j列的商品重量;m、n表示立体仓库每排共m层n列。
(3)堆垛机存取货物是多目标优化求解问题,通过对两个目标函数赋予权重参数,使得多目标函数变成单目标函数进行求解。为了方便计算求解,两个目标函数权重参数均为0.5。将上述目标函数进行变换可得到函数:
f3=0.5·(f1+f2),
(4)
在赋予权重参数后,可得到堆垛机最终的目标函数:
(5)
2 立体仓库货位优化模型算法设计
自动化立体仓库出入库路径优化通过研究其出入库任务的执行顺序,并为每一个货物分派货位,以提高立体仓库的效率和利用率[5]。
2.1 遗传算法介绍
遗传算法是近几年迅速发展的一种高效的优化算法。算法对目标函数的形状、连续性等无特殊要求,条件要求不严格,且具有很好的全局搜索能力、良好的容错能力以及适应性。遗传算法不只限于局部搜索仅仅记录一个解,而是记录一个群体,它可以同时记录多个解。考虑到遗传算法在小规模的多目标优化项目中具有运算速度和精度上的优势,采用遗传算法对立体仓库的货位进行优化[6]。
2.2 遗传算法设计
通过建立模型、设计编码、确定适应度、遗传操作以及仿真进行立体仓库货物分配算法设计。在整个货位优化过程中,堆垛机在货品和货位之间起着纽带作用,即每一个货品都是通过巷道堆垛机被运送到优化后的货位上。入库货位优化的研究对象就是货品、货位和巷道堆垛机。模型的建立需要将研究对象的客观属性抽象化,从而全面考虑货品、货位和巷道堆垛机三者之间的关系,找出各个实体之间的相关属性。为了求解方便,不考虑货物的大小以及形状。
(1)确定编码。遗传算法编码就是其中的转化方法,编码的好坏将极大地影响立体仓库的响应速度、货位优化的复杂程度以及货位优化的效果等。由于立体仓库属于多目标组合优化问题,通过对比发现整数编码更加有效,因而选用整数编码。具体方式如下:①一组货位的优化由一条染色体代替;②染色体上的每个基因数与立体仓库优化的货位区间中货位数相对应,每条基因可由多个数字组合而成;③染色体上的每个基因代表着一个货位,该基因所在染色体的位置代表货位在该处的编码。研究的货位为单独的一个货架,因此采用两个整数x、y表示行和列。假设目前有4个货物需要存放在优化区间内,相应的编号如表1所示。由表1可知,(1,1)表示将编号为1的货物存放在坐标为(1,1)的货位中。(1,1)(2,3)(3,2)(4,1)表示一条染色体上的基因,把该基因放在一起表示一条染色体,即一组货位的最优解。
表1 货位对应编码

货物编码对应数字编码1(1,1)2(2,3)

货物编码对应数字编码3(3,2)4(4,1)

12345…货物(1,1)(2,3)(3,2)(4,1)(5,2)...货位
(2)种群初始化。种群的数目设定为随机,种群数目越大,遗传算法得到最优解的机会就越小。考虑执行效率和结果,将种群的数目设定为100。
(3)适应度确定。遗传算法中对适应度函数的要求为非负,且适应度要求越大越好。通常会将目标函数作为适应度函数,但由于选择策略的影响,需要适应度函数非负递增。本节所研究的货位优化目标为两个,并且都要求取最小值,且函数值非负。对于求最小值的函数问题,目标函数和适应度函数可以通过以下变化:
(6)
对于Cmax为一个较大的数,∀f(x),Cmax≥f(x)。Cmax取值可以由以下方法取得:①预先设定较大固定值;②当代所得的最大适应值;③当前或几代中最大适应值。
由于要求的目标函数纲量不同,对于目标函数直接进行加权求和显然没有意义。因此解决纲量不同带来的影响,需要对目标函数进行去纲量处理。
对目标函数进行如下的线性变换法转换:
fk=αfk+b
其中a,b的线性比例如下:
(7)
由式(7)得到去纲量后的适应度函数:
(8)
式中,k表示第几个目标函数。
对式(8)取倒数,得到适应度函数:
(9)
为了使得上述函数能够在区间(0,1)中,对于遗传算法通常采用正规标定的方法:
(10)
γ∈(0,1)在此区间内,避免分母为0;将选择方式调整为随机选择。通过去纲量和正规标定处理后,目标函数均为无纲量和映射在(0,1)区间的函数。
将多目标函数取权重wk且权重之和为1,最终将两个适应度函数化为一个适应度函数:
(11)
式中,wk为目标函数纲量;Fk为一个适应度函数。
(4)选择策略。选择算子:遗传算法的选择影响着种群的发展,遗传算法中较常用的方法主要有轮盘赌选择法、随机遍历抽样法等。由于轮盘赌选择法具备操作简单,不同的选择算子会使算法表现不同的性能的特点,采用轮盘赌选择算子。假设种群规模为N,个体的适应度为Fk,那么该个体可能被选中的概率为P。
(12)
由式(12)可以看出,采用轮盘赌的方法与该个体的适应度有关,适应度越大,则越容易遗传到下一代中。
交叉算子:采用较多的单点交叉法对染色体进行交叉运算,交叉原理如图3所示。

图3 遗传算法交叉原理
变异算子:遗传算法通过交叉操作后得到大量相同的染色体,很容易收敛到局部最优解。所以在遗传算法得到的最优解中随机选择两个基因进行位置交换;计算换位后的染色体适应度是否减少或者增加,如若发生减少则取用换位后的个体取代原个体。重复上述两个步骤,达到事先规定的交换次数。
2.3 货位优化仿真及求解
(1)货位优化模型建立[7]。建立的立体仓库货架货位10排10列共计100个货位,每个货物托盘所占货位均为1,同时有5种货物需要入库,相关参数如表2所示。

表2 货物参数
(2)仿真结果对比分析。用Matlab遗传算法求解,所得优化前后结果分别如图4、图5所示。由图4、图5可知,通过不断迭代,优化后的曲线较未优化的曲线下降更为平缓。优化后的货位在240代以后目标函数基本没有变化,迭代完成时的值为4.45×105,迭代时间为104.562 s。优化前的货位目标函数在275代之后基本没有变化,迭代完成时的值为4.68×105,迭代时间为204.529 s。

图4 优化前货位求解结果 图5 优化后货位求解结果
3 立体仓库堆垛机路径优化
堆垛机的作业过程就是从起始点到目标点完成取送货后再回到起始点的过程。堆垛机执行该工作的过程所走的轨迹即为堆垛机拣选路径。立体仓库堆垛机的路径优化[8]即实现堆垛机在拣选货物时行走路程最短。
3.1 立体仓库拣选货物作业建模
对于堆垛机拣选问题的研究,通常将其假设为商旅问题进行描述:有N个城市,一个旅行商从起始城市出发,到另一个城市买货,之后到其余未曾到过的城市买货,最终N个城市全部买完回到起始城市,要求旅行商所走路径最短。用数学模型可表达为:
(13)
式中,Si为城市号;d为城市之间距离。
堆垛机在拣选作业时,程序给予作业任务,堆垛机根据作业任务从起始点处出发,依次将作业清单上的任务拣选完成后回到拣选作业区,以便执行下次任务。
3.2 拣选路径优化计算仿真
利用改进后的遗传算法针对企业要求进行算法求解。拣选货物坐标参数如表3所示。根据表3中的参数,利用Matlab进行求解计算,最终得到优化结果如图6所示。通过Matlab计算得到结论:优化前一批货物从开始拣选到拣选结束所用时间为385.71 s,改进后所用时间为235.69 s。堆垛机的作业时间明显缩短,提高了堆垛机的工作效率。

表3 拣选货物坐标参数

图6 优化前后路径
4 结论
通过对立体仓库的分析,解决自动化立体仓库的货位优化问题和堆垛机路径优化问题[9]。通过算法选择,确定优化目标和约束条件,建立相应的数学模型,结合遗传算法思想,并对遗传算法进行一定的优化,利用Matlab求解。最后,通过对比优化前后的结果,实现了自动化立体仓库的货位优化和堆垛机路径优化[10],提高了自动化立体仓库工作效率。
