基于盲源分离的ICAICA去噪技术在裂缝预测中的应用

2019-04-25王有涛桂志先

数据采集与处理 2019年2期

王有涛桂志先

（1.油气资源与勘探技术教育部重点实验室（长江大学），武汉，430100；2.中国石化胜利油田分公司勘探开发研究院，东营，257000；3.长江大学地球物理与石油资源学院，武汉，430100）

引言

近年来，盲源信号分离在理论研究和算法研发方面都取得了长足的进步，在一些实际生产领域得到了很好的应用[1-4]。但是对盲源信号分离技术的研究尚不成熟，有关理论研究和实际应用需要进一步研究。独立分量分析方法（Independent component analysis，ICA）[5-7]是在盲源信号分离原理的基础上发展而来的多维信号处理方法，简单来说就是通过一定原则建立目标函数，利用优化算法将观测信号分解成许多个相互独立的成分。

地震记录在采集过程中，有效信号和干扰信号均被接收到，因此地震信号处理中去噪过程是重要环节。由于地震记录中有效信号和干扰信号满足独立分量分析技术的非高斯分布，而且统计上保持独立，可以对地震信号利用独立分量分析技术开展噪声消除。许多学者在这方面也开展了相关的研究应用，刘喜武等[8-9]将盲信号分离在地震信号去噪和反褶积中的应用可行性进行了分析；贾瑞生等[10]利用独立分量分析方法对微震信号进行降噪处理，提取微震有效信号；杨宝俊等[11]论述了基于独立分量分析的多次波消减技术；吕文彪等[12]提出了基于独立分量分析的叠前地震资料单频噪声压制的方法，有效保护相同频段范围的有效波，提高资料信噪比。

本文基于盲源分离技术，将地震资料分解为不同级次的背景与储层目标反射响应，进而将能够反映储层裂缝特征的有效信息提取出来，可以较为直观地进行裂缝发育带描述和预测。

1 基于盲源分离理论的ICA去噪技术

盲源信号分离[13]是指从观测的多道混合信号分离并恢复出每个独立源信号的过程。盲源分离技术是对信源和信道毫无任何先验知识或者知道很少的情况下，仅仅通过观测到的信号提取需要的特征信号或者是恢复出观测信号各个相对独立的成分，这也是盲信号处理得到更多关注应用的亮点。在实际情况下获取先验信息是非常困难或者过程耗费大量资源，同时，实际工程中的信号满足盲源分离中要求的源信号最多有一个高斯分布，其余均为非高斯分布的要求。独立分量分析[7,14]是近年来逐步发展起来的信号处理新算法。其过程是将信号分解成许多个独立的成分，实现信号的增强和分析。假设某个信号是由一些独立的信号源混合而成，要将这些信号源分离，单一通道的观察无法做到分解。独立分量分析技术通过多导信号处理的方法，利用信号源混合成的多道同步观察可以做到较好的分离。独立分量分析和盲源分离具有相似的算法，只不过盲源分离研究的范围更广，独立分量分析是盲源分离的核心技术。

独立分量分析是对n个相对独立的未知源信号S(t)=[s1(t),s2(t),…,sn(t)]T，经过未知信道的传输，在m个传感器上获取观测数据向量X(t)=[x1(t),x2(t),…,xm(t)]T。在此假定传输是瞬时的（即为ICA瞬时模型），也就是说不同的信号到达每个传感器的时间差别可以忽略不计，并且传感器接收到的是各个原始信号的线性组合，即认为第i个传感器的输出为

式中：aij为混合系数，sj(t)为第i个原始信号。式（1）可用矩阵表示为

式中：A为n×m维的矩阵，第i行、第j列的元素为aij，称为混合矩阵。则ICA问题就表述为在混合矩阵A和源信号S均未知的情况下，只是利用传感器接收到的信号X，尽量真实地分离出源信号S，即可通过建立一个分离矩阵W=(wij)n×m，使W对混合信号X(t)作线性变换Y(t)=WX(t)，得到源信号S(t)的一个可靠估计，那么，ICA问题的求解就可表示为

式中：G为全局系统矩阵。假设经过学习使G=I（I为n×n单位矩阵），则Y(t)=S(t)，从而实现了对源信号的分离（恢复或估计）。

通过以上建立模型的过程可以发现，盲源信号分离存在多解的问题，即针对一组观测信号X(t)有可能存在多个不同的混合矩阵A与源信号S(t)。为使得ICA问题有确定的解，需要做一些符合实际工程应用的假设和约束条件。在本文研究中，为了达到去除噪声的目的，将非高斯随机噪声也看作源信号的一部分，对它与其他“真实的”源信号的混合信号进行盲分离处理，实现分离噪声和有效信号的目的，且这样的算法适用范围更广、稳健性更强。

随机变量采用ICA分离后，能够使得各个分量间最大限度地接近统计独立，即认为各个分量具有最强的非高斯性。根据极大似然估计的原理，满足非高斯分布的含噪随机变量，在噪声方差较小的情况下，其非高斯性越强则估计越准确。所以先对含噪的资料进行ICA分离，能够有效地增强信号的非高斯性，这样再通过极大似然估计就能达到减少估计误差的目的。基于这些特性，将ICA技术与稀疏编码(Sparse coding,SC)算法结合，简称ICA-SC算法。

含噪ICA模型为X=AS+N，共中N表示噪声且通常假设其为高斯噪声。通过极大似然估计的方法做正交ICA分解，可得到估计的分离矩阵W，可将式X=AS+N转换为

式中：W为正交矩阵，即通过ICA估计混合矩阵A的最佳正交逆矩阵；而干扰项WN仍然满足高斯分布且白化。通过ICA变换能够使得各个分量满足非高斯，故ICA技术与SC理论的交点就在于通过ICA变换使得目标数据满足稀疏分布的要求。值得一提的是拉普拉斯分布就是典型的稀疏分布，这恰恰即为ICA变换的优势所在。

假设目标数据x满足单位方差，则典型的拉普拉斯的概率分布为

式中：s为尺度函数，记为s=E{x2}。

根据目标数据（稀疏分量）的概率分布，求解稀疏惩罚函数的一阶导数，再代入极大似然估计公式得到对应的收缩函数，求解如下

式中l(x)为稀疏惩罚函数。极大似然估计表达式为

将式(5，7)代入式(8)，可以得到拉普拉斯密度模型对应的收缩函数

式中σ2表示目标数据中噪声的方差。

通过式（9）可知，稀疏编码理论去噪的原理是根据有效信号的非高斯性（该模型为拉普拉斯分布）及噪声信号的高斯性中假设了噪声信号满足高斯分布，通过收缩函数达到压制噪声的目的。

ICA-SC算法的计算机实现步骤如下：

（1）采用ICA方法估计一个正交矩阵W，对目标数据x左乘W，使得ICA变换后的数据xˆ=Wx满足稀疏分布；

（3）对正交矩阵 W 求逆，得到 e=W-1。

2 ICA技术在地震资料去噪中的应用

地震资料信噪比是决定数据有效性的基础，而随机噪声是影响资料信噪比的重要因素。真正意义的高斯信号具有良好的性质，一般多用于理论研究，而实际资料中，很少有绝对满足高斯分布的信号。地震资料中有效信号反映地下地质体的信息并具有一定的连续性，而随机噪声则无固定频率与视速度，因此可以认为两者彼此统计独立。根据以上论述，现假设实际地震记录中的有效信号和随机噪声均为源信号，并且两者都有统计独立与非高斯分布的特征。这样就可以通过ICA技术对地震记录中的有效信号与噪声进行分离。

2.1 仿真实验1

图1（a）为随机产生、满足非高斯分布的300个样点，视为反射系数序列。子波设为主频为40 Hz的Ricker子波，子波的长度为81。

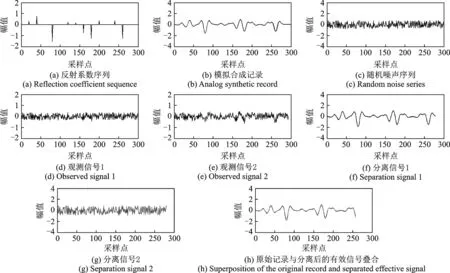
图1 一维仿真信号的ICA去噪效果分析Fig.1 Analysis of ICA denoising effect of one-dimensional simulation signal

通过将反射系数序列与Ricker子波褶积，得到长度为300个样点的模拟地震记录，如图1（b）所示。图1（c）为随机产生、服从非高斯分布的序列，含有300个样本值，将该序列作为随机噪声。将随机噪声序列与模拟的合成记录按随机生成的矩阵进行混合后作为实际记录到的观测信号如图1（d）和图1（e）所示。

采用ICA技术对观测到的两个信号进行信噪分离，结果如图1（f）和图1（g）所示，进一步将分离后的有效信号与模拟生成的原始记录叠合在一起显示，如图1（h）所示。由此可以看出经过分离后的信号较好地保持了原始信号的波形特征，一致性较好。在被噪声淹没的观测信号中实现了信噪分离的目标。根据地震信号的模拟实验结果，表明ICA技术可应用于去除地震资料中的随机噪声。

2.2 仿真实验2

为更好地说明ICA技术的分离性能，使用含噪多道模型来验证，模拟水平层状介质和楔形体褶积模型如图2（a）所示。

对加噪后（SNR=2 dB）的地震记录图2（b）采用ICA技术进行信噪分离，具体处理的过程是：取宽度为5的时窗，对时窗内的5道记录做加权平均，并把加权平均后的结果作为标准道与时窗内的第1道做ICA分离。分离后的结果采用与单道模型相同的操作，与标准道求相似系数，相似系数绝对值大的记为有效信号，并根据结果的正负来判断是否发生极性变化。

将分离出的有效信号作为第1道，以步长为1滑动时窗，重复上述操作，分离的有效信号作为第2道，依此类推，分离出的有效信号和噪声结果分别如图2（c,d）所示。通过对比图2（c,d）不难看出，ICA技术能够有效地分离噪声与有效信号，提高了剖面的信噪比。将该方法的去噪结果与常规去噪方法的效果也进行了对比分析。图2（e,f）分别是利用f-x域去噪技术和小波软阈值去噪技术去噪后的结果。从去噪效果可以看出，图2（c）的去噪效果明显优于图2（e,f）效果，这3种方法去噪后的信噪比分别为6.5,3.5,4.6，说明了该方法的有效性。

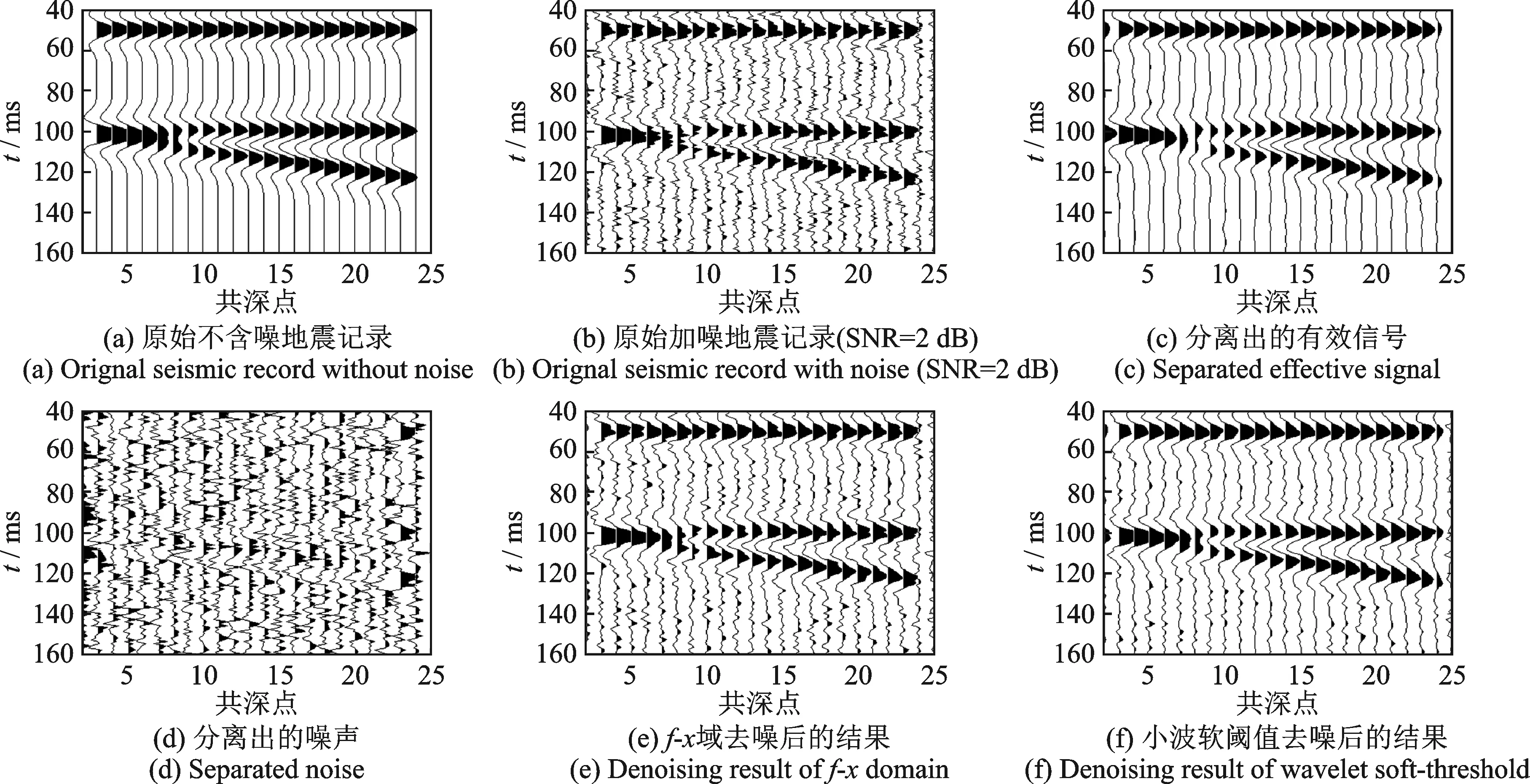
图2 二维仿真信号的ICA去噪效果分析Fig.2 Analysis of ICA denoising effect of two-dimensional simulation signal

3 ICA去噪技术在车排子地区应用效果分析

近年来，准噶尔盆地车排子地区石炭系勘探取得了较好的勘探成果，展示了该区石炭系火成岩储层的勘探潜力，裂缝预测是描述火成岩储层的关键环节。本次研究利用该区三维地震数据体进行了基于盲源分离的ICA去噪处理，并在此基础上开展裂缝预测应用。

图3展示了过P615井测线盲源分离技术的去噪效果。对比图3（a—c）可以看出，随着盲源分离技术多级分离得到的有效信号信噪比明显增强，地震资料反射同相轴变得连续，横向波形特征的稳定性得到提高。对比地震资料的频谱特征图3（e,f）看出，二级盲源分离处理后的地震资料相对于原始地震资料的资料品质得到了较好的提高，增强了地震资料对地质信息的刻画能力。图3（d）为分离出来的随机噪声，基本不含有效信号，从而有效保证了去噪后有效信息基本不受损失。

图3 过P615井测线地震资料去噪效果Fig.3 Seismic data denoising effect of crossing well P615

利用去噪后的地震数据体，采用结构导向梯度属性边缘检测方法开展P6井区裂缝发育带的检测，图4，5分别是去噪前后沿石炭系顶面进行边缘检测结果的对比图。结合地质构造分析，研究区内发育近南北向P61断层和北西向P68断层，断裂附近裂缝相对较为发育，其中P637井钻遇安山岩和凝灰岩荧光显示44.1 m，岩心观察见较多微细裂缝，未被充填；P614井钻遇大套凝灰岩，二级荧光显示24.8 m，岩心观察见较多微细裂缝，少量被方解石充填；P621井钻遇致密凝灰岩，有较多微细裂缝发育，少量方解石充填；在两条断裂附近的P610井钻遇凝灰岩和凝灰质泥岩，受断裂影响，凝灰质泥岩亦发育少量微细裂缝。应用效果表明，在ICA去噪的基础上进行边缘检测的效果优于原始地震数据的检测结果[15-16]，裂缝发育特征特别是具有一定规模的断层，横向定位更加准确，与断裂发育特征一致性较好，在横向展布上连续性更好。

图4 原始地震数据体沿石炭系顶部裂缝检测结果Fig.4 Detection results of the fracture along the top of the carboniferous system by the original seismic data

图5 盲源分离去噪后沿石炭系顶部裂缝检测结果Fig.5 Detection results of the fracture along the top of the carboniferous system by the blind source separation and denoising seismic data

图6 P69井区石炭系顶面裂缝发育带预测Fig.6 Prediction of fracture zone for the top carboniferous system of P69 well field

在ICA去噪的基础上，采用基于倾角扫描的曲率属性[17-18]，对P69井区石炭系顶面裂缝发育带进行了预测，提高了裂缝发育带预测的可靠性。图6是P69井区石炭系顶面裂缝发育带预测结果，其中图6（a—c）分别是基于倾角扫描的大尺度曲率属性（对应的α=0.5）、中尺度曲率属性（对应的α=1）和小尺度曲率属性（对应的α=2）平面分布。对比剖面和平面图可以看出，大尺度曲率属性反映了地层的弯曲以及主要的区域断层分布情况，中小尺度曲率属性则反映了断层、构造上的微妙变化，较好地刻画出研究区裂缝发育带。