基于压缩感知的电能质量压缩采样重构算法

张 锐 吴庭宇

（哈尔滨理工大学自动化学院，哈尔滨，150080）

引 言

随着科学技术的不断发展、进步，智能电网已经成为电网技术发展的必由之路，保障电网安全、可靠、稳定的运行是智能电网的必然要求[1]。这无疑提高了获取高质量的电网电能质量信号数据的要求，由于传统的电能质量信号数据采集受到奈奎斯特(Nyquist)采样定理的约束，使得想要恢复原信号必须要求采样频率为信号最高频率的2倍以上，这样就会采集大量的数据，而且获得的很多数据都是无用的，不仅对采样设备的要求较高，而且对数据的传输也有很大的负担。因此，研究一种低采样率的技术对电能质量信号的检测，分析和处理具有重要的意义和前景。

压缩感知理论(Compressed sensing,CS)正是在这样的背景下由Donoho等人[2-4]提出来的，该理论使得以较少的采样点恢复出原信号成为了可能。CS理论为信号处理领域打开了一扇新的大门，它突破了Nyquist采样定理对传统信号采集的限制，因此该理论一经提出就受到图像处理、医疗成像、地质勘探、雷达探测等领域专家学者的高度关注，而且还被美国科技评论评为“2007年度十大科技进展”[5-7]。

本文主要研究的是电能质量扰动信号的重构算法。在压缩采样匹配追踪算法(Compressive sampling matching pursuit,CoSaMP)[8]的基础上，针对CoSaMP算法预选阶段对候选原子选择过多、测量次数多、重构时间长的问题，提出一种改进的压缩采样匹配追踪(Modified compressive sampling matching pursuit,MCSMP)电能质量扰动信号重构算法。该算法改变了候选集的选择方法，并以感知矩阵与残差的相关度变化阈值作为迭代停止的条件[9]，MCSMP算法不仅可以减少重构时间，而且还可以提高电能质量信号的恢复质量。

1 压缩感知重构算法

1.1 压缩感知理论基础

假设信号x是电能质量原始信号，为了不失一般性，假设x本身不是稀疏的，而是可稀疏化的，其在稀疏基Ψ上的投影为θ，即

式中：x为信号在时间域的表达；θ为其在变换域Ψ上的表示，而且θ中只有Κ个非零项，其他Ν-Κ个项为零。那么就可以认为信号x在稀疏变换矩阵Ψ下的表示是稀疏的，θ的稀疏度为Κ，当使用观测矩阵Φ对x进行观测时，可以得到观测值

式中：Α为感知矩阵。这样就把对原信号x的重构问题就转化成对稀疏信号θ的求解，再通过稀疏反变换得到x。由于Μ＜Ν，因此该式为欠定方程组，没有确定解，是NP-Hard问题。当感知矩阵Α满足有限等距性质(Restricted isometry property,RIP)[10]时有

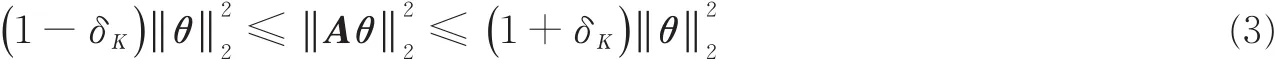
式中δΚ∈(0,1)。上述问题可以转化为l0范数下的最优化问题

若考虑到误差δ，δ为一个较小正常数，则可以写成

或者是转化为l1范数下的凸优化问题

压缩感知理论框架主要由信号稀疏变换基、观测矩阵和重构算法构成，它们分别被看作是压缩感知理论的基础前提、关键和核心。

1.2 信号稀疏基的选择

作为压缩感知理论实现的前提，稀疏变换基的选择主要有离散傅里叶变换基(Discrete Fourier transform，DFT)，离散余弦变换基(Discrete cosine transform，DCT)，离散小波变换基(Discrete wavelet transform，DWT)和冗余字典等[11]，由于原信号为电能质量信号，其在频域上的稀疏性较好，考虑到傅里叶变换的正交性，而且具有构造简单，速度快，表示过程复杂度低的特点，因此，稀疏基选择傅里叶变换基。

1.3 观测矩阵的选择

观测矩阵是压缩感知实现的关键，前面提到压缩感知高概率重构的保证是感知矩阵要满足路由信息协议（Routing information protocol，RIP）条件，实际情况是要验证一个感知矩阵是否满足RIP条件较难，不过已经证明：感知矩阵的RIP条件等价于观测矩阵与稀疏基高度不相关[12]。因为独立同分布的高斯随机矩阵与大部分稀疏基的不相关度很高，具有普适性，所以本文中的观测矩阵选择高斯随机矩阵。

1.4 重构算法的选择

鉴于解决不同范数的优化问题所采用的方法不同，压缩感知的重构算法主要分为：基于解决l0范数最小化的贪婪算法、基于解决l1范数最小化的凸优化算法和一些组合算法。其中凸优化算法的重构效果较好，但是计算比较复杂，运算时间较长，而组合算法重构时间短，但是重构效果不好，贪婪算法凭借其计算速度快，重构效果较好备受广泛使用。贪婪匹配追踪类算法主要有匹配追踪算法(Matching pursuit，MP)[13]，采用了正交化的正交匹配追踪算法(Orthogonal MP，OMP)[14]，以及在它们基础上发展起来的加入了正则化的正则化正交匹配追踪算法(Regularized OMP，ROMP)[15]与带有回溯选择的CoS-aMP等。

由于CoSaMP算法有二次选择原子的能力，可以剔除初次选择中错误的原子，所以选择其作为电能质量扰动信号的重构算法，并且针对CoSaMP算法存在的不足，对原算法进行优化改进，提出了MCSMP算法。

2 基于MCSMP的电能质量重构算法

2.1 CoSaMP算法

CoSaMP算法是以OMP为基础发展的一种贪婪迭代追踪算法，该算法通过对候选集的初步选择，支撑集的二次选择确定，通过最小二乘法对原信号不断估计逼近，完成重构原信号的目的。具体算法步骤如下。

输入：观测矩阵Φ，稀疏变换基Ψ，观测值y，稀疏度Κ。

输出：重构的原信号x。

步骤1初始化，残差r=y，索引值集合C=空集，F=空集，迭代次数t=1。

步骤2计算感知矩阵与当前残差的内积，并在内积的绝对值中选出最大的2Κ项存入集合C，C=

步骤3更新候选原子集合Ft=[Ft-1,C]。

步骤4最小二乘估计

步骤5支撑集的裁剪，从集合b中挑选出绝对值最大的K项存入θ，并且相应更新Ft中的原子。

步骤6残差更新，信号估计，rt=y-Αθ，x=Ψθ。

步骤7循环停止判定，若是满足迭代的停止条件t＞Κ，那么停止迭代并输出重构信号，如果不满足，执行t=t+1，并返回步骤2。

2.2 MCSMP算法

2.2.1 候选原子的选择

CoSaMP算法在每一次循环迭代时，对候选原子的选择原则都是选择残差与感知矩阵内积绝对值最大的2K个原子，而这些原子中大部分都是错误的原子，在支撑集的确定时会通过回溯的方式被裁剪掉，这样不仅增加了计算复杂度，增加了算法重构的计算时间，甚至还会影响到重构精度。对于稀疏度越大的信号影响越大，针对这一问题，受到分段弱阈值共轭梯度算法[16-17]的启发，采用模糊阈值的方法代替CoSaMP算法中对候选集原子选择的固定数量方式

式中：c为模糊阈值，a和b为可设置的模糊阈值参数，rand(1)的作用是生成0到1之间的随机数。因为每次迭代时，由残差新引出的原子数目很小，相比于CoSaMP每次选择2K个原子，采用模糊阈值的选择方式更合理。一般a取0.6～0.8之间的数值，b取0.8～1之间的数值，使用这种选择方式，可以有效减少候选集原子初选时的错误率，而且为后续支撑集原子的裁剪减少了计算量，同时减少了算法的运算时间。

2.2.2 迭代停止条件的确定

CoSaMP算法的终止迭代条件过于依赖稀疏度K，需要循环迭代K次之后才会终止循环，然而实际情况是很多时候，在迭代次数没有达到K时，信号就可以精确重构了，继续迭代不仅增加了迭代时间，而且也有可能影响重构精度。针对这一问题，MCSMP算法采用感知矩阵与残差的相关度变化阈值为迭代停止条件。在每次循环迭代时计算感知矩阵与当前残差相关度的最大值wt，并将其同上一次循环迭代时感知矩阵与残差相关度的最大值wt-1相比较，如果它们的差的绝对值小于一定阈值γ，那么就终止循环，如果不满足就继续循环。这样通过改变迭代停止条件就可以高效地减少循环计算次数，进而提升重构速度。

2.2.3 MCSMP算法步骤

输入：观测矩阵Φ，稀疏变换基Ψ，观测值y，稀疏度Κ。

输出：重构的原信号x。

步骤1初始化，残差r=y，索引值集合C=空集，F=空集，迭代次数t=1。

步骤2计算感知矩阵与当前残差的内积，并根据模糊阈值选出符合条件的项存入C，C={| Αj,rt-1|≥ cmax| Αj,rt-1|},j=1,2,…,N。

步骤3更新候选原子集合，Ft=[Ft-1,C]。

步骤4最小二乘估计bFt=y，=0，其中=(ΑFt)-1。

步骤5支撑集原子裁剪，选出b里面绝对值最大的K项存入θ，并相应更新Ft。

步骤6根据当前残差rt=y-Αθ，计算感知矩阵与当前残差的相关度wt，wt= max| Αj,rt|。

j=1,2,…,N

步骤7如果满足终止条件|wt-1-wt|＜γ，那么停止循环并输出重构信号，如果不满足，t=t+1，返回步骤 2。

3 实验仿真结果及分析

3.1 实验环境

为验证MCSMP算法的正确性和有效性，本文在MATLAB R2013a实验仿真平台上，根据国家标准生成常见的电能质量扰动信号样本，如电压暂升、暂态振荡、电压尖峰、电压凹陷、谐波和电压波动等。并根据MCSMP重构算法步骤编写代码，对生成的各扰动信号样本进行采样重构测试。采样频率参数设置成1 600 Hz，基波频率为50 Hz，样本信号长度为320，观测值的维数为96。由于参数a,b和γ的选择会影响到MCSMP算法重构的质量和重构所用的时间，为了确定合理的参数值，使用不同的参数值对随机生成的不同稀疏度的信号样本进行1 000次实验，实验结果表明：把模糊选择阈值的参数设置成a=0.8，b=0.95，控制停止迭代的参数值设置为γ=10-6时，可以在保证重构效果的前提下有效地减少重构时间，所以，本文中所有实验MCSMP算法的参数设置均如上所述。

3.2 重构波形

上述几种电能质量扰动信号的原始信号波形，重构信号波形和重构误差波形图分别如图1—8所示。

图1 电压暂升信号MCSMP算法重构信号和重构误差Fig.1 MCSMP reconstruction signal and reconstructionerror of the voltage swell signal

图3 电压中断信号MCSMP算法重构信号和重构误差Fig.3 MCSMP reconstruction signal and reconstructionerror of the voltage interruption signal

图2 电压暂降信号MCSMP算法重构信号和重构误差Fig.2 MCSMP reconstruction signal and reconstructionerror of the voltage sag signal

图4 暂态振荡信号MCSMP算法重构信号和重构误差Fig.4 MCSMP reconstruction signal and reconstructionerror of the voltage oscillation signal

由图1—8可知，MCSMP算法能够以较小的误差，良好地质量重构各电能质量扰动信号，其中，电压波动重构误差均值为0.001 2 pu，短时谐波重构误差均值为0.019 6 pu，其余扰动信号重构误差均值则在两者之间。

图5 短时谐波信号MCSMP算法重构信号和重构误差Fig.5 MCSMP reconstruction signal and reconstructionerror of the short-time harmonic signal

图7 电压凹陷信号MCSMP算法重构信号和重构误差Fig.7 MCSMP reconstruction signal and reconstructionerror of the voltage notch signal

图6 电压尖峰信号MCSMP算法重构信号和重构误差Fig.6 MCSMP reconstruction signal and reconstructionerror of the voltage spike signal

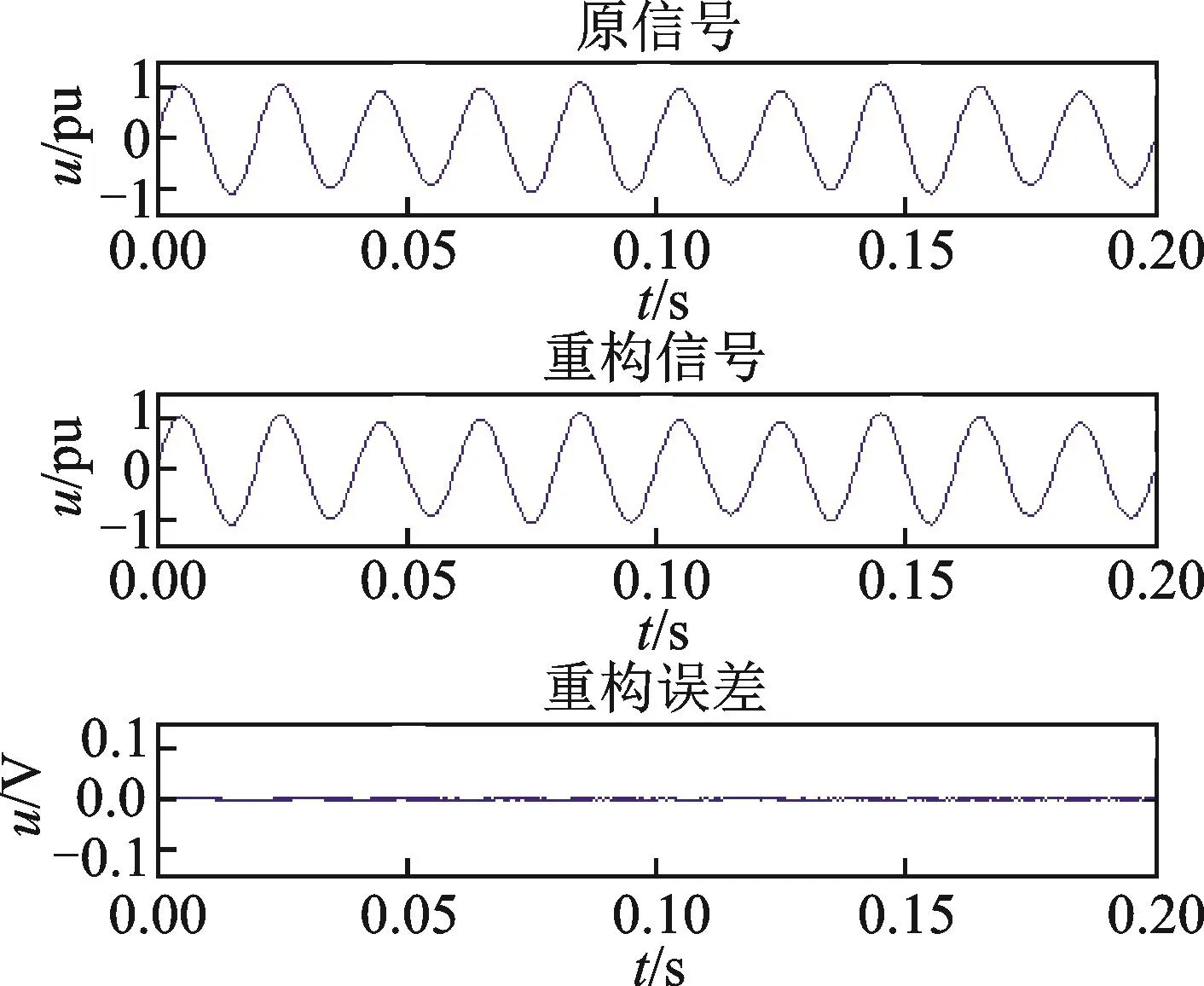
图8 电压波动信号MCSMP算法重构信号和重构误差Fig.8 MCSMP reconstruction signal and reconstructionerror of the voltage fluctuation signal

3.3 评价指标

为了能够更客观科学地分析MCSMP算法的重构性能，利用以下性能指标对各种扰动信号的重构效果进行定性评估。

（1）重构信噪比（Signal-noise ratio，SNR）

式中：x(i)为原信号，xˆ(i)为重构信号，N为信号长度，下同。

（2）均方误差百分值（Mean-square error，MSE）

（3）能量恢复系数（Energy-recovery percentage，ERP）

3.4 MCSMP算法重构结果以及性能分析

使用MCSMP算法对各种电能质量扰动信号样本分别进行100次仿真重构实验，计算各自的平均评价指标，结果如表1所示。从表1中能够明显看到MCSMP重构算法对以上几种电能质量扰动信号样本的重构性能指标较好。除了短时谐波外其他电能质量扰动信号的重构信噪比均在30 dB以上，均方误差百分值都在4.00%以下，能量恢复系数差值均在1.5%以内，能够以很小的能量损失重构原始信号。

3.5 与其他重构算法性能对比

为了验证MCSMP算法在重构速度上的改进效果，采用改进前后的两种算法分别对信号长度Ν=256，观测值维数Μ=150，信号稀疏度为K的随机信号进行采样重构，稀疏度K取10～54之间的数值（稀疏度K大于54之后CoSaMP在N=256，M=150的条件下无法进行有效的重构），每个稀疏度K各进行100次实验，算出每个稀疏度K的平均运行时间。

从图9中可以明显看出，当稀疏度K＜42时，两种算法对信号重构所需要的时间非常接近，MCSMP算法的重构速度稍微慢一点，而当稀疏度K＞42之后，CoSaMP算法重构所需要的时间不仅比MCSMP算法多，而且以较大的速率快速增长，相比之下，MCSMP算法重构所需时间的增长就非常缓慢。也就是说，随着稀疏度增大，MCSMP算法在重构速度上的优势就会越来越明显。而且在本次实验中，当稀疏度K＞54之后，CoSaMP算法无法对信号样本进行有效的重构，而MCSMP算法却依然可以，说明MCSMP算法改进方法有效。

继续对比MCSMP算法与其他同类重构算法对电能质量扰动信号进行重构时的性能表现，以电压暂升信号为样本信号，将MCSMP算法与CoSaMP算法、ROMP算法和OMP算法在相同的实验条件下分别对电压暂升信号样本进行重构仿真实验，各个评价指标均为实验100次的平均值，具体指标如表2所示。

从表2中可以看出，在相同的实验条件下对电压暂升扰动信号进行重构，MCSMP算法的重构信噪比为44.35 dB，比其他3种算法的重构信噪比都高，均方误差百分值是4种算法中最低的，能量损失也较小，在重构速度上只比ROMP算法稍慢，比其他两种算法快。由此可见，改进后的MCSMP算法能以较高的信噪比，较低的均方误差百分值和较快的速度完成对电能质量扰动信号的重构。

进一步分析4种算法对电压暂升信号重构的信噪比与均方误差百分值随观测值变化的变化趋势。每个观测值对应的信噪比与均方误差百分值均为100次实验的平均值。如图10和图11所示，信噪比随观测值的增加而增加，而均方误差百分值随观测值的增加而减小，当观测值低于120时，两者均变化较大，观测值大于120时趋于稳定。对于4种算法来说，当观测值小于120时，观测值的数量对于重构性能的影响较大。从图10与图11两个指标图中能够明显看出，MCSMP算法的重构性能在两个性能指标曲线图中都是最好的。

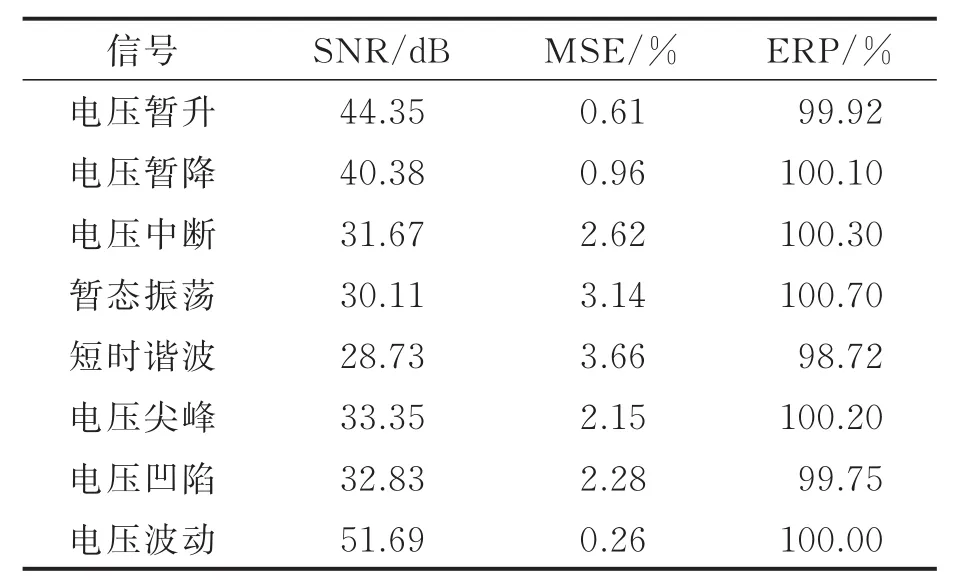
表1 MCSMP对电能质量扰动信号重构性能指标Tab.1 Performance index of power quality disturbance signal reconstructed by MCSMP

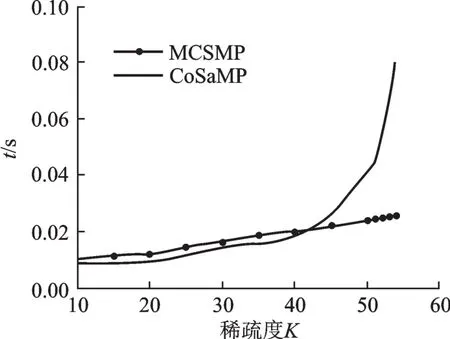
图9 MCSMP算法与CoSaMP算法不同稀疏度下的平均运算时间比较Fig.9 Comparison of the average operation time under different sparsity of MCSMP algorithm and CoSaMP algorithm

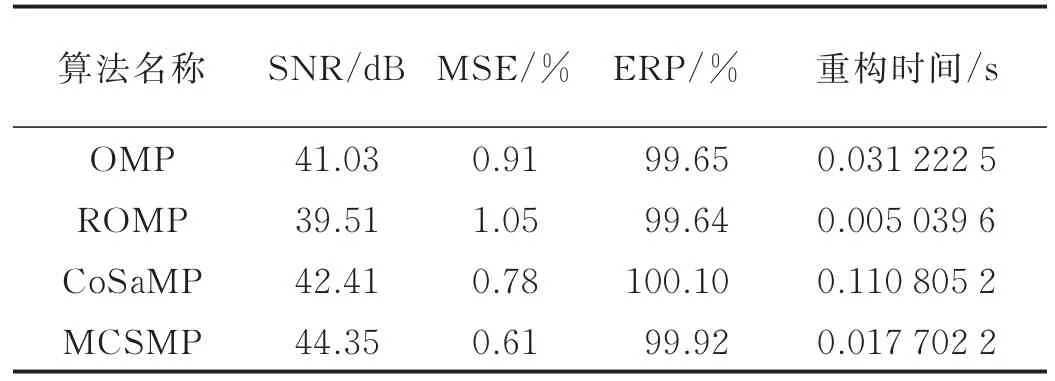
表2 各算法电压暂升重构性能指标对比Tab.2 Reconstruction performance comparison of the voltage swell signal under different algorithms

图10 电压暂升信号在4种算法下信噪比随观测值变化曲线Fig.10 Changing curves with measurements of SNR of voltage swell signal under four algorithms

图11 电压暂升信号在4种算法下均方误差百分值随观测值变化曲线Fig.11 Changing curves with measurements of MSE of voltage swell signal under four algorithms

4 结束语

本文介绍了CS理论基础，并针对CoSaMP算法存在的不足，提出改进的MCSMP重构算法，主要做了两个方面的改进：（1）采用模糊阈值的方法替代了CoSaMP算法中固定个数的原子选择方式，为算法后续的裁剪减轻了负担；（2）使用残差与感知矩阵相关度的变化量作为算法的迭代停止条件，避免了原算法在重构时进行不必要的迭代，进而提高了算法的重构速度。然后将MCSMP算法应用在电能质量信号的重构上，并与同类的其他算法进行重构性能的对比实验,具体结果为：

（1）采用MCSMP算法对常见的几种电能质量扰动信号进行重构测试，仿真实验的重构性能指标结果表明：MCSMP算法能够在满足信号分析要求的条件下高质量重构常见电能质量扰动信号。

（2）分析MCSMP算法与CoSaMP算法的运行速度，实验结果表明：稀疏度较小时两者运行速度差距不大，稀疏度大于42之后，MCSMP算法有较大的速度优势。又对比了同类别的其他算法，MCSMP算法在信噪比SNR，均方误差百分值MSE，能量恢复系数ERP和重构时间上都有较好的性能表现。

电能质量扰动信号具有较大的带宽，按照Nyquist采样定理需要采集大量的数据，给数据的采集、传输增加了负担与成本，鉴于电能质量信号在频域有较好的稀疏性，故将CS理论应用到电能质量信号的采集与重构上。本文提出的MCSMP算法能够以较少的观测点重构电能质量扰动信号，实现信号采样和压缩的完美结合，重构效果较好、速度快，对于电能质量扰动信号重构算法的发展有很大的促进作用。考虑到实际工程应用中电能质量信号的稀疏度通常无法获得，所以研究一种可以自动匹配不同稀疏度的重构算法是笔者下一步的研究方向。