永磁同步电机改进型电流预测控制策略研究
2019-04-25肖海峰
肖海峰
(西安航空学院,西安 710077)
0 引 言
永磁同步电机伺服系统对负载的快速响应取决于电磁转矩响应能力。因此,响应电流跟踪参考电流的能力是电流环性能的重要指标。
永磁同步电机系统的电流控制策略大致采用比例积分控制、滞环控制或先进智能控制。比例积分控制和滞环电流控制都存在着鲁棒性较差的问题[1-4]。神经网络解耦控制、自适应控制算法等先进智能控制策略可以明显改善电流环控制动态性能[5-8],但仍存在转矩脉动和算法复杂等缺点。
电流预测控制具有严谨的数学推导、良好的动态性能及跟踪无过冲特点[9-10],各国学者已对该技术在逆变电源、电机控制等领域的应用做了大量研究。永磁同步电机电流预测控制的思想是利用当前时刻计算出的电压参考预测下一时刻的控制电压,通过价值函数选择最优的控制信号,使下一个采样周期结束时电流误差为零,但该策略的前提是需要一个精准的电机模型,且需要克服电机模型参数失配对预测控制的影响。文献[11]利用在线辨识参数的方法校正电机数学模型,减小电感参数失配对控制性能的影响,但不能避开系统扰动对参数辨识的影响。文献[12]采用平滑输出电压实现电机预测控制,增强了电机模型预测对参数失配的鲁棒性,但削弱了预测控制的部分动态性能[13-14]。
为增强传统电流预测控制的鲁棒性,本文研究了一种改进的永磁同步电机电流预测控制方法,引入电流补偿因子,通过对电机期望参考电压偏差在线修正的方法,抑制了模型参数失配对系统性能的影响,同时改善了电流环鲁棒性。在模型参数感抗失配条件下,对比研究了补偿前后的系统性能,仿真和实验表明,改进后的策略减少了系统对电感参数精度的依赖,提高了电流预测控制精度,增强了系统的鲁棒性。
1 永磁同步电机电流预测控制
1.1 离散状态空间数学模型
表贴式永磁同步电机在同步旋转坐标系中,选择交、直轴电流为状态变量,假设在kT和(k+1)T之间输入电压和反电动势保持不变,因此状态空间表达式如下:
状态方程式(1)的离散通解如下式:
式中:
令t=(k+1)T-τ,则:

x(k+1)=Hx(k)+Mu(k)+N(k)(4)
1.2 电流预测控制
永磁同步电机离散时间模型k时刻的电流方程:
x(k)=Hx(k-1)+Mu(k-1)+N(k-1)(5)
假设在一个采样周期内电机反电动势保持不变,则:
N(k-1)≈N(k)(6)
将式(4)、式(5)代入式(6),有:
u(k)=u(k-1)+M-1[x(k+1)-x(k)]+
M-1H[x(k)-x(k-1)] (7)
当前时刻电流采样值x(k)可直接获得,u(k-1)和x(k-1)可以从上一周期中得到,如果将x(k+1)用参考电流x*(k+1)代替,则可以预测出当前时刻的控制电压:
东南亚既是理论意义上的传统儒家文化圈,也是新老华侨的最大聚集地。儒家文化圈是指文化相近、历史上受中国政治及中华文化影响的覆盖日韩及东南亚部分地区的文化区域。一方面,作为传统的儒家文化圈,主动对东南亚进行体育交流,容易在这一地区产生中国的体育影响力,特别是作为传统文化的武术,更容易为这一地区的人们所接受,从而扩大传播的影响力;另一方面,东南亚又是华人移民海外的最大聚集区。在中国近代史上,中国曾有过四次大的移民潮,分别是蹚古道、闯关东、走西口、下南洋。其中的蹚古道、闯关东、走西口,基本都限制在国内迁徙,唯有下南洋是部分中国人为谋生而闯荡海外。
u(k)=u(k-1)+M-1[x*(k+1)-x(k)]+
M-1H[x(k)-x(k-1)] (8)
将电流参考值作为下一个周期的电流预测值,就可得到定子电压的参考值,电流将在第k+1次采样时刻跟踪上参考状态,即x(k+1)=x*(k+1),实现了电流环的无差拍控制。
2 永磁同步电机模型误差分析
令定子电阻失配值为ΔR,电流预测模型其他参数不变。令直轴电流id=0,得到电机交轴电流的给定值与参考值之间的关系:
(9)
根据离散系统稳定条件,必须满足:
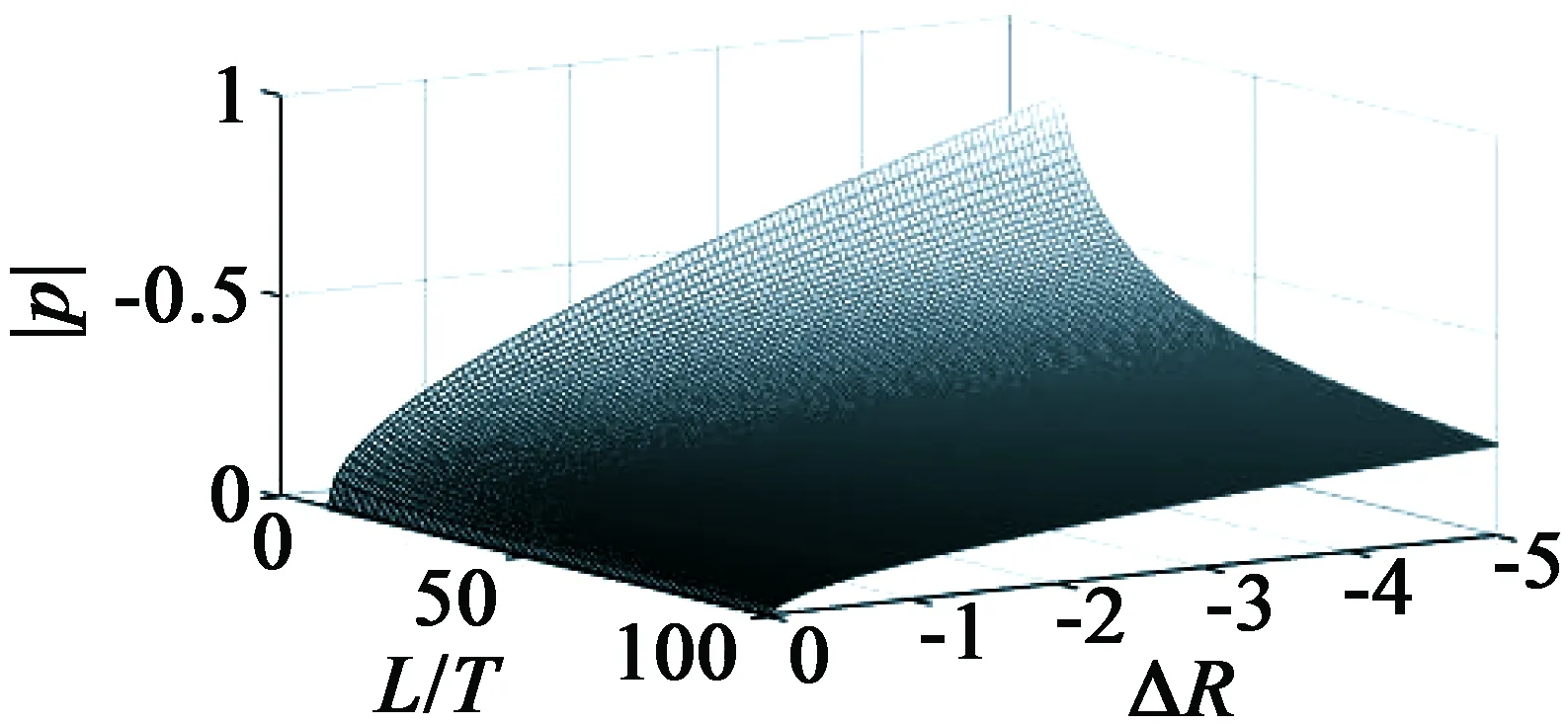
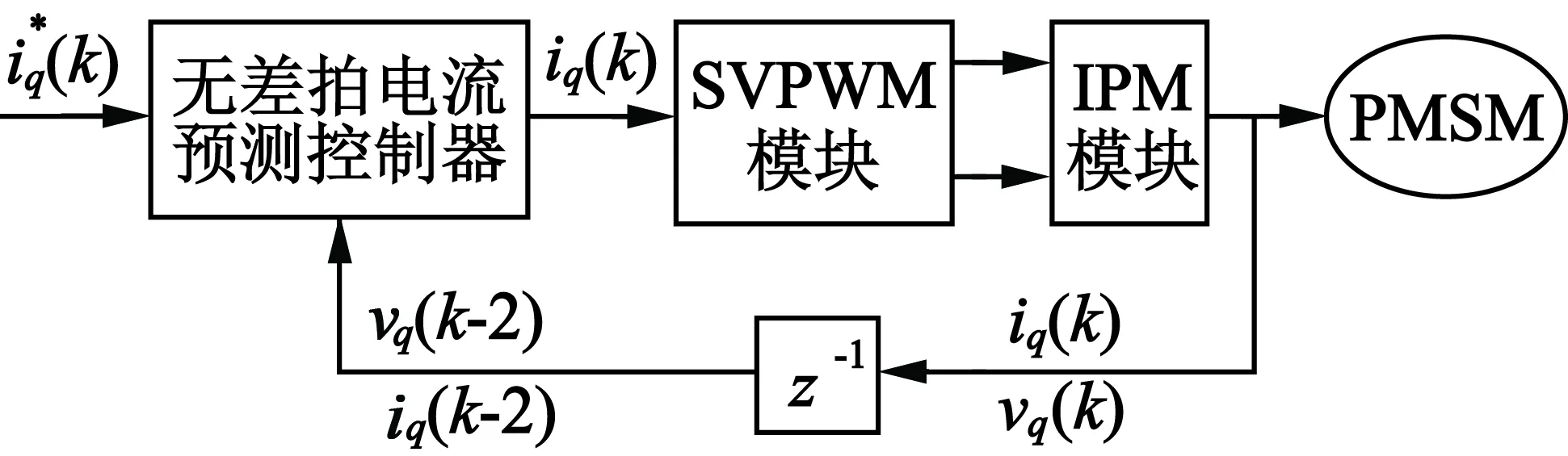
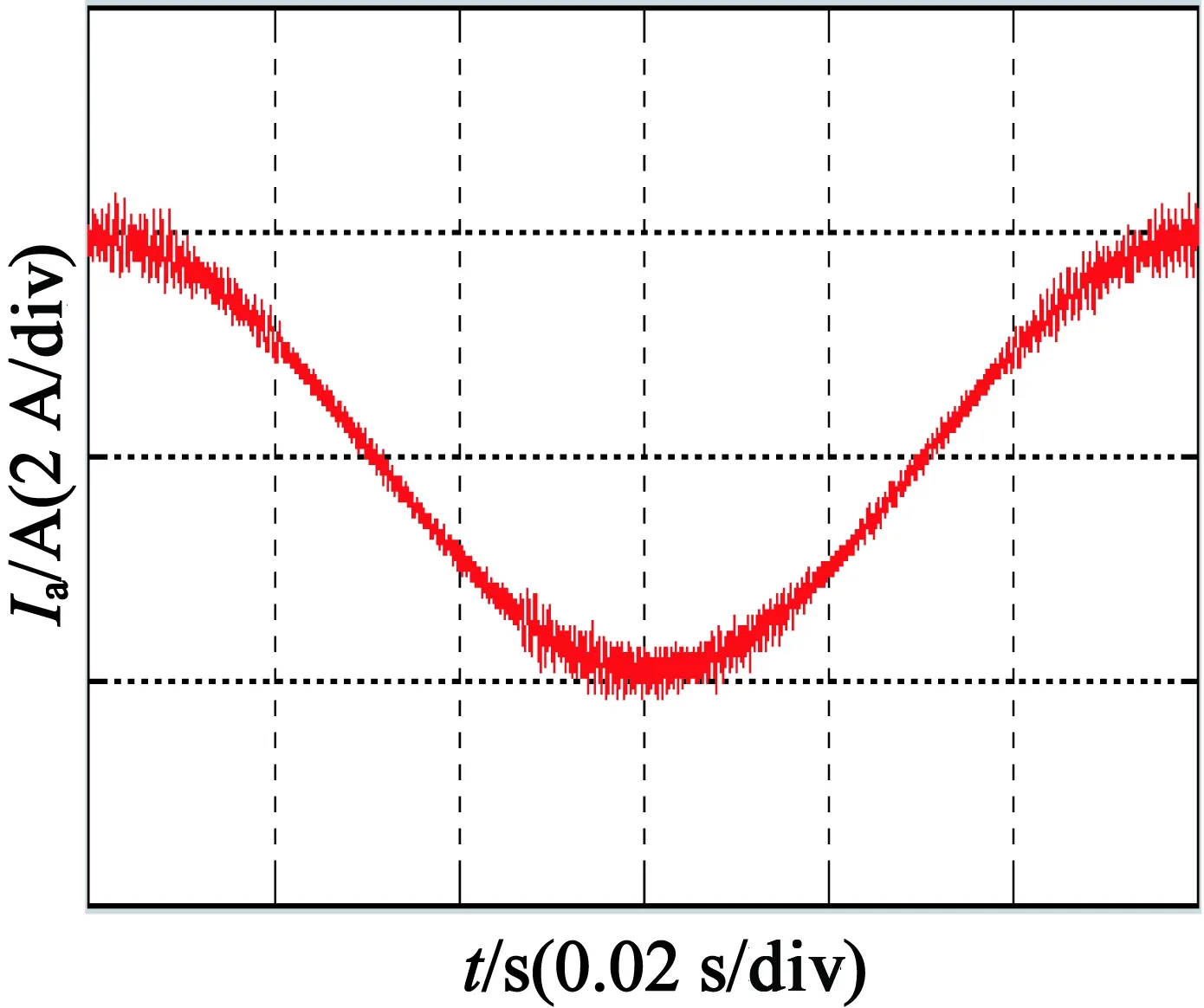
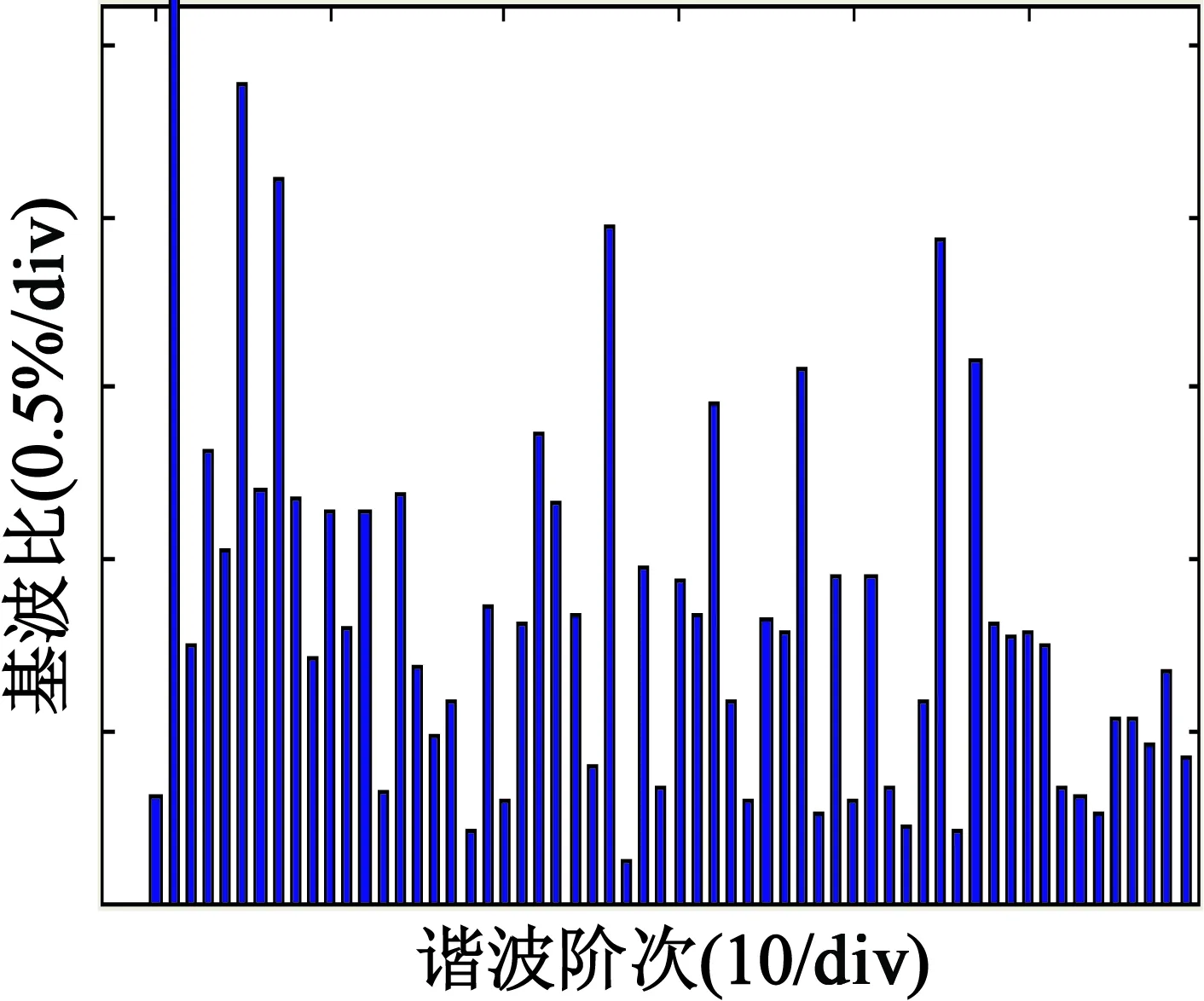
-L/T< ΔR ΔR,L/T与极点p1,p2的关系,如图1所示,系统的稳定性受到ΔR,L/T之间比例关系的制约。如果定子电阻误差增大且接近于L/(2T),主导极点p2将靠近z平面单位圆边界,电流响应将产生较明显的振荡过程;反之,定子电阻误差趋近于零,则电流阶跃响应振荡过程短暂且超调较小。 (a) |ΔR|,L/T与p1的关系 (b) |ΔR|,L/T与p2的关系 当-L/T<ΔR<0时,在z平面单位圆内存在一对共轭复数极点,极点模|p|,ΔR和L/T的关系如图2所示,ΔR和L/T相等时,极点模|p|=1,输出电流信号为等幅振荡序列。如果定子电阻误差绝对值接近于L/T,主导极点接近单位圆边界,电流响应出现较明显的振荡过程并逐步稳定于参考输入;反之,定子电阻误差绝对值趋近于零,则电流阶跃响应迅速且超调较小。 图2 极点模值|p|,ΔR和L/T的关系 (11) (12) 在z域传递函数: (13) 在电机电压方程中引入γ为补偿系数,且满足0<γ<1,对k时刻的电机定子期望参考电压进行偏差修正,故参考电压方程可表示: 补偿后的参考电压与预测参考电压相等,即: (16) 将上述离散模型转换到z域下,其传递函数: (17) 在上述离散域传递函数中,可以利用补偿系数γ抑制定子电感参数变化引起的电流环系统的不稳定,使电流预测控制的鲁棒性增强,其电流控制模型如图3所示。 图3 改进型电流无差拍预测控制模型 忽略逆变器、采样滤波器等硬件系统延迟,仅考虑一个PWM控制周期延时的改进型无差拍电流预测控制模型如图4所示。由于输出电压不大于线电压,因此根据无差拍电流预测算法得到的输出电压矢量必须进行幅值限制,令母线电压为udc,而电流预测控制模型是在同步旋转坐标系中实现的,故最大输出电压值为2udc/3。 图4 电流环控制结构 利用MATLAB/Simulink验证改进型无差拍电流预测控制算法的有效性,选取永磁同步电机为1.5 kW, PWM开关频率为15 kHz。 当L0/L=1.2时,即电感参数估计值大于实际值的20%,引入补偿系数γ=0.8,两种无差拍电流预测控制策略定子电流响应及频谱分析如图5、图6所示。改进前后电流预测模型电流总谐波畸变率变化较小,分别为4.67%和3.40%,通过引入电流预测无差补偿项,抑制了定子电流畸变。因此,当电感参数估计误差较小时,两种无差拍电流预测控制都可以使系统获得较好的稳定性,且电流谐波引起的畸变差别不大。 (a) 传统算法 (b) 改进型算法 (a) 传统算法 (b) 改进型算法 当L0/L=1.8时,图7、图8为两种无差拍电流预测控制策略定子电流响应及频谱分析。当电感参数发生较大偏差时,传统无差拍电流预测控制策略得到定子电流产生明显畸变,转矩脉动较大,严重影响了电机系统稳态性能,如图8(a)所示,电流总畸变率达到10.41%。引入电流补偿因子后,即选取补偿系数γ为0.8,无差拍电流预测控制策略对电感参数失配具有较强的鲁棒性,如图8(b)所示,电流总畸变率达到5.06%,输出电流谐波成分得到有效抑制,改进后的策略有效减小了转矩脉动,提高了系统的鲁棒性。 (a) 传统预测算法 (b) 改进型预测算法 (a) 传统预测算法 (b) 改进型预测算法 永磁同步电机传统无差拍电流预测控制系统性能受到电感参数误差的影响,只有当电感误差较小时电流畸变小,随着电感估计误差增大,系统变得不稳定,通过引进补偿系数的无差拍电流预测控制策略能够有效抑制电流畸变,使系统表现出良好的快速性及鲁棒性。 根据上述内容搭建的永磁同步电机调速系统实验平台,选用的实验电机与仿真模型电机参数一致,PWM控制周期为1/15 000 s,微处理器TMS320F28335的系统时钟频率为150 MHz,电流采样等其他电路均可满足电流预测控制所需的硬件条件。 无差拍电流预测控制电感参数失配比达50%时,传统补偿策略下的电流稳态响应波形如图9所示。补偿后电机相电流畸变依然严重,相电流过零钳位,电机转矩脉动明显,FFT分析得到电流总畸变率达9.3%, 主要是5、7次谐波分量,同时含有系统开关频次噪声。 (a) 电流稳态响应曲线 (b) 频谱分析 在相同的电机电感失配条件下,电流补偿因子γ=0.56,采用改进后的电流预测控制,电流稳态响应曲线及频谱分析如图10所示,电流畸变得到有效抑制,没有明显的电流过零钳位现象,通过FFT频谱分析可知,电流总畸变率为4.5%,其中5、7次谐波分量相对减小,开关频次噪声也得到有效抑制。 (a) 电流稳态响应曲线 (b) 频谱分析 当电机电感参数失配值在较小的范围内,传统电流预测控制策略可以为调速系统提供较好的动态响应能力及稳定性。电感失配比达两倍以上,传统电流预测控制策略将不能满足系统稳定性要求,通过引入电流补偿因子,可提高电流预测控制方法的鲁棒性,削弱了电流预测精度对参数估计误差的影响。 本文在永磁同步电机模型旋转坐标系下,对永磁同步电机的电流预测控制算法进行了研究。传统无差拍电流预测控制方法具有数学结构简单、电流响应快的特点,但对模型参数失配敏感,鲁棒性较差。针对上述问题,研究了改进型无差拍电流预测控制,能够有效地提升系统的鲁棒性,引入的补偿系数能够明显降低电机参数估计误差对系统性能的影响,同时保持了传统无差拍控制算法的优点。仿真分析及实验结果表明,电机电流总谐波畸变率降低,抵抗负载扰动的能力更强,具有更好的动、静态特性。

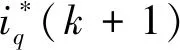

3 无差拍电流预测控制改进算法


4 仿真及实验结果
4.1 仿真验证分析





4.2 实验验证分析




5 结 语
