基于半张量积压缩感知的形变数据重构在航天器结构健康监测中的应用
2019-04-25田引黎杨林华张鹏嵩曹海林
田引黎,杨林华,张鹏嵩,曹海林
(1. 重庆大学 微电子与通信工程学院,重庆 400030;2. 北京卫星环境工程研究所,北京 100094)
0 引言
近年来,航天器结构逐渐趋于大型化和复合材料化,对航天器性能的要求也逐渐提高,安全问题日益突出。航天器工作环境恶劣且难以维护,一旦发生事故,损失惨重,若能对航天器结构故障进行有效诊断,将会减少航天器飞行事故的发生。因此,实时监测航天器的结构健康状况意义重大。结构健康监测(structural health monitoring, SHM)可以实时监测航天器健康状况,及时提示对航天器的损伤进行维护,从而降低发生航天事故的风险。实时SHM主要是从传感器采集大量数据,并提取能够预测结构健康状况的相关特征。随着无线传感网络技术的发展,使得前端不间断采集数据成为可能,然而大量数据的传输和存储成为无线传感网络面临的主要挑战。因此,人们一直在探索新的方法,希望能减少数据的储存和传输量,以减轻无线传感网络的储存压力,从而延长无线传感网络的生命周期。
传统的数据压缩方法采用先采样后压缩的方式,虽然可以减少传输数据的容量,但是并没有减少采集数据的容量。针对这一不足,Donoho[1]提出了采集和压缩同时进行的方法——压缩感知(compressed sensing, CS),可大量节省信号采集占用的储存空间。但CS的应用需要满足2个条件:1)信号满足某种特定的稀疏性;2)观测矩阵满足有限等距性[2]。实际上,大部分自然信号都是稀疏的或者在某种变换基下是稀疏的,因此CS技术一经提出即引起广大研究者的兴趣,被广泛应用于智能电网、电子鼻等各个领域[3-4]。也有相关文献将CS用于SHM:应用CS进行桥梁加速度信号的压缩采样[5];应用CS对无线传感器网络进行数据修复[6];应用CS对振动信号进行监测与诊断,以减小数据的存储量[7];将CS应用在Lamb波SHM中,以降低测量信号的存储量[8]等。由于CS重构必须满足有限等距性,而随机矩阵具备优良的不相干特性[1],所以随机矩阵是目前CS应用的普适观测矩阵。但随机观测矩阵在实际使用过程中,通常具有占用内存多、计算复杂度高等局限性。鉴于此,半张量积压缩感知(semi-tensor product compressed sensing,STP-CS)方法[9]被提出,这是一种泛化的CS,突破了传统CS矩阵相乘时的维数一致限制。
本文应用STP-CS技术,以航天器翼梁形变监测为例,首先采用离散余弦变换(DCT)对形变数据的稀疏性进行研究,然后利用降维的随机高斯矩阵对形变数据进行压缩采样,最后通过正交匹配追踪对采集的数据进行重构,验证该方法的有效性。该方案旨在缩小观测矩阵的存储空间,为解决航天器SHM的储存和传输量过大问题提供理论支持。
1 基于STP-CS的航天器形变数据压缩采样模型
以航天器形变数据为例说明STP-CS的算法流程。
设长度为n的航天器形变信号x∈Rn×1,通过STP-CS模型[10]

测量得到压缩采样后的航天器形变信号y∈Rm×1,其中Φ代表观测矩阵。
如果航天器形变信号在时间域不具有稀疏性,可以通过变换域将其转换成稀疏信号
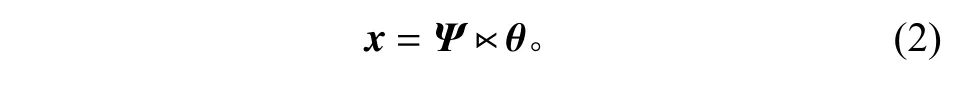
其中:Ψ为变换矩阵;θ为稀疏矩阵。将式(2)代入式(1)可得:
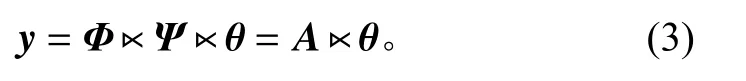
当t=1时,式(3)即为传统的CS模型。
2 航天器形变数据重构
CS重构一直以来都是研究的热点,目前已经有很多成熟的重构方法,大体分为3类:1)凸优化方法,如l1范数,该类方法具有较强的重构性能,但是所需时间比较长;2)贪婪算法,如正交匹配追踪,该类方法相比于凸优化算法,运算时间短,但是重构性能相对较弱;3)迭代阈值算法,该方法运算时间和重构性能都位于前二者之间。考虑到航天器SHM的实时性要求比较高,本文选择正交匹配追踪作为航天器形变数据重构的算法[9]。基于正交匹配追踪重构的航天器形变数据算法流程如下:
1)输入:压缩采样后的航天器形变数据为y∈Rm×1,传感矩阵A∈Rm×n,迭代次数K。

3 实验验证
基于STP-CS的航天器结构监测系统形变数据的采集过程如图1 所示,具体可以分为4步:
2)将采集到的航天器形变数据流ym×1进行无线传输;
3)在接收端即对接收到的数据ym×1进行重构,采用正交匹配追踪算法恢复出变换域的稀疏数据;换,获得重构后的航天器形变数据。
4)对变换域的航天器形变稀疏数据进行逆变
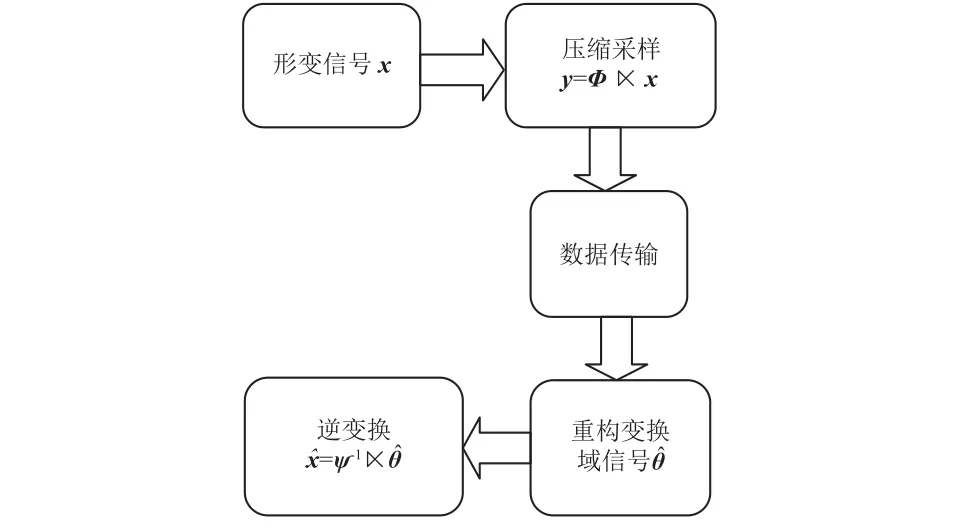
图1 基于 STP-CS 的形变数据压缩采样及重构流程Fig. 1 Flow chart of deformation data compressed sampling and reconstruction based on STP-CS
3.1 基于离散余弦变换的稀疏变换
为了验证该算法在航天器SHM中的可行性,本文选取航天器机翼形变信号作为研究对象,但由于获取实测航天器机翼形变信号较难,本文以桥梁形变信号的挠度信号近似替代进行研究。航天器机翼形变指的是机翼与大气相互作用产生升力时,通过翼梁将所承受的力传递给机体,在力的作用下机翼会发生一定的形变[11]。而桥梁结构形变指的是桥梁结构长期受到外界因素的影响会产生形变[12]。二者都是因为外界影响产生形变,当形变过大时,将会导致灾难发生。因此,桥梁形变信号与航天器机翼形变信号具有一定的相似性。桥梁挠度是指桥之梁在载荷作用下不同位置处所产生的竖向变形[13]。本文选取了1024个桥梁挠度数据进行处理,如图2所示。
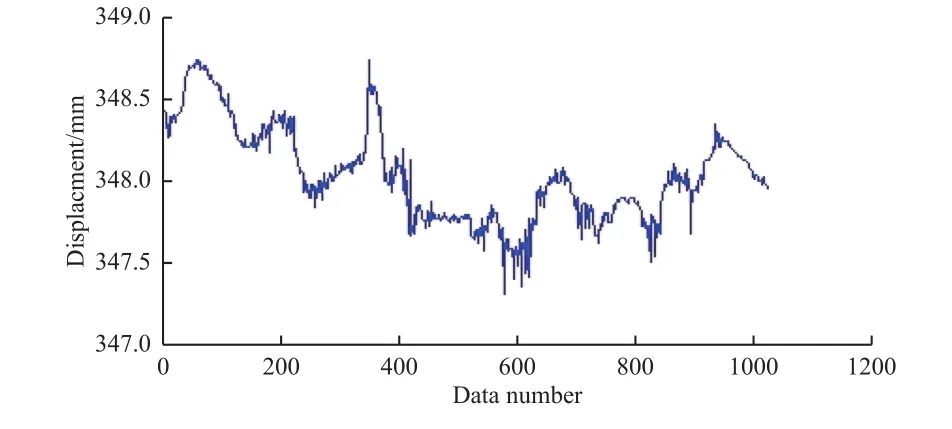
图2 挠度信号Fig. 2 Deflection data
由图2可知,挠度信号在时域并不稀疏,需要找到适合该信号的稀疏基,对其进行变换,使之在变换域是稀疏的。本文采用DCT对挠度信号进行变换,变换效果如图3所示,可见变换后的挠度信号在DCT域具有稀疏性。
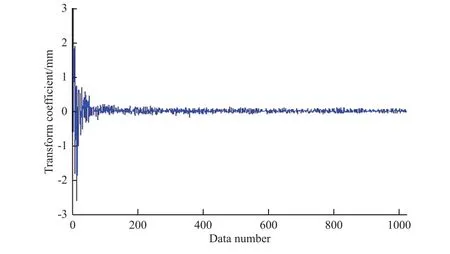
图3 DCT 变换后的挠度信号Fig. 3 Deflection signal after DCT transformation
3.2 重构性能的评估
为了评估重构性能的优劣,本文采用相对误差R作为衡量指标,

由于随机矩阵具有良好的不相干性,本文选取随机矩阵作为观测矩阵。为了验证STP-CS观测矩阵的低储存性,我们分别取观测矩阵维数为传统CS观测矩阵维数的1、1/2、1/4、1/8倍,观测矩阵储存空间为传统 CS观测矩阵的 1、1/4、1/16、1/64,即t=1、2、4、8。当t=1时,该算法等同于传统 CS。重构效果如图4所示,可见随着观测矩阵维数的降低,即观测矩阵存储空间的减小,重构误差有所增大,但并不明显。
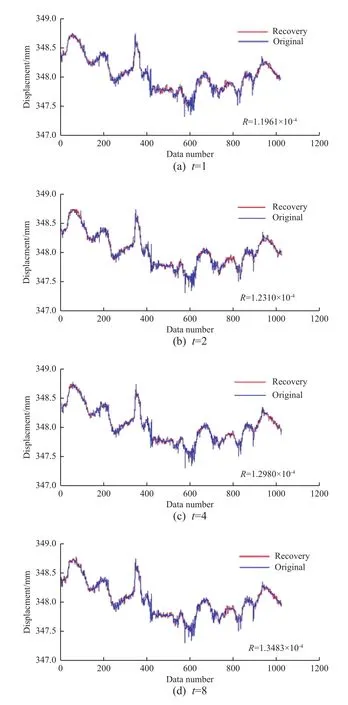
图4 采用不同观测矩阵维数时的信号重构效果Fig. 4 Signal reconstruction by using different observation matrix dimensions
图5所示为基于STP-CS的形变数据重构的重构时间与观测矩阵维数的关系,显然随着观测矩阵维数的降低,重构时间也在不断缩短。

图5 采用不同观测矩阵维数时的重构时间Fig. 5 Reconstruction time in using different observation matrix dimensions
4 结束语
为了解决航天器SHM面临的数据储存和传输量过大问题,本文应用STP-CS模型进行采样数据降维。实验数据验证结果表明:采用该方法在减小观测矩阵储存空间的同时仍能以较高精度重构压缩采样数据,而且随着观测矩阵维数的降低,重构时间也在不断缩短;但随着观测矩阵维数的降低,重构误差会有所增加,换言之,储存空间和重构时间的减少是以增加重构误差为代价的。如果在可接受的误差范围内采用该方法进行压缩采样及重构,可以有效减少采样数据和传输数据量,缩减储存空间和重构时间,提高航天器SHM的效率。
