反射面天线结构振动下的电性能分析方法

邓润然，邹元杰，葛东明，杜敬利

（1. 北京空间飞行器总体设计部，北京 100094；2. 西安电子科技大学 机电工程学院，西安 710071）

0 引言

随着航天技术的快速发展，大型高精度遥感平台的研发需求激增，在资源勘探、环境监测、地产评估、海洋开发、气象预报等领域都有着极为广泛的应用前景。很多遥感平台采用了反射面微波天线，天线在电性能方面对精度、稳定度指标提出了苛刻的要求，有关机电耦合问题也呈现出多样性和复杂化的特点。一方面，卫星平台在轨运行过程中，将受到卫星工作模式、太阳电池阵光照、空间碎片冲击等多种载荷作用，天线的结构形状将发生静态变形或动态结构振动，进而影响天线的电性能指向[1]。另一方面，对于我国正在研制的带大型反射面天线航天器、超大容量通信卫星，为保障通信安全以及观测可靠，对天线的指向精度和稳定度都有极高的要求。然而，航天器姿态机动、太阳电池阵驱动以及进出地球阴影的冷热交变均可能导致天线结构产生振动，严重影响天线的指向精度和姿态稳定度。研究结构振动对天线电性能影响的直接关系可以有效评估天线观测能力，预估天线保形要求或根据电性能影响程度进行结构振动控制与电性能补偿。目前，国内外对反射面天线电性能与结构变形的集成建模与分析开展了很多研究工作，主要针对天线反射面的型面误差或静态变形对天线电性能的影响。对于结构型面系统误差和随机误差，静力载荷作用的结构变形等问题，目前从理论方法到工程软件分析都已有很好的解决方案。Ruze最早对误差影响进行了研究，建立了天线增益下降与反射面表面光程差之间的关系[2]。目前很多研究人员应用这种方法获得型面的变形进而得到天线型面变形后的误差均方根，并采用Ruze公式计算反射面误差造成的天线增益损失。王从思、段宝岩等[3]针对地球引力、热、风等载荷，研究最佳吻合抛物面设计方法，通过求解线性方程组得到最佳吻合抛物面，从而确定系统误差分布；并基于口径场法的反射面型面误差、馈源误差与电性能之间影响关系，推导出一套机电耦合模型。GRASP、FEKO等工程软件都能够很好地完成天线电性能与结构的耦合建模，分析结构变形对电性能的影响[4]。但是，以上处理方法都更加适用于解决静态变形问题[5-7]。而星载反射面天线的在轨工作过程中的振动变形，既不属于无规律的随机误差，也非静态变形，而是与卫星的工作模式关系密切，以上处理方法将无法满足需求。葛东明等[8]给出了带大型天线的卫星在轨集成柔性与姿轨控一体化模型，基于此模型分析振动过程对天线指向的影响，但给出的仅是机械指向，不足以描述振动对天线电性能的影响。杜平安等[9]提出了一种随机振动下的天线机电耦合分析方法，但是未对卫星在轨工作模式下的结构振动对天线电性能的影响进行研究。

本文针对反射面天线振动过程的电性能分析问题，实现了结构振动与电性能集成建模，给出了从反射面天线结构振动到电性能增益的直接近似关系式，可得到振动过程中反射面天线的电性能变化情况，弥补了当前电性能分析仅可针对于单次静态结构变形展开的不足。

1 结构振动与电性能集成建模

1.1 电磁场模态空间离散

天线在轨结构振动在力学分析中是可以按照模态空间展开的，结构振动变形是多种不同频率振动的叠加，以结构各阶模态作为基函数，即可将时域振动离散为频域空间的振动。在工程处理中，可通过相应截取准则对有效模态进行截取，从而降低计算量，同时保证较好的计算精度。按照这种分析思路，如果可以将天线振动过程的电性能在频域空间展开，得到模态坐标对应的基函数，而这种基函数实际可认为是某种静态变形下的天线电性能参数，那么天线振动过程中的电性能则只需要获取结构振动的模态坐标即可求解。

首先，获取天线主轴方向系数对表面节点位移的导数列向量与二阶Hessian阵，将天线主轴方向系数描述为表面节点位移的二次近似关系式

式中：G为天线主轴方向系数；G0为理想状态下的天线主轴方向系数；Δr为表面节点位移；L为天线主轴方向系数对节点位移的一阶导数列向量；H为天线主轴方向系数对节点位移的二阶Hessian阵。L、H可以描述为：

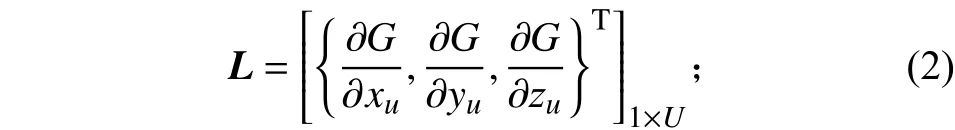
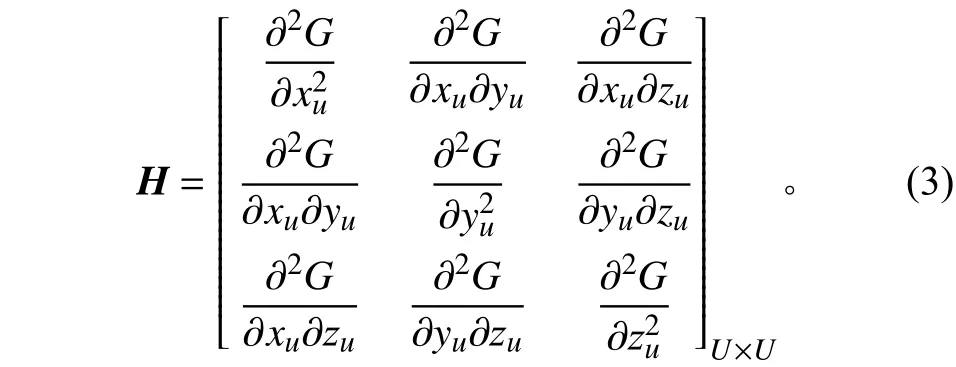
其中：xu、yu、zu分别为反射面节点u的3个方向的坐标；U为节点总数。

又有天线结构动力学分析方程

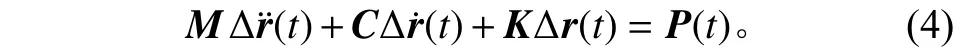
其中：M、C、K分别为结构质量、阻尼和刚度矩阵；、Δr分别为各节点组成的加速度、速度和位移列向量；P为作用在天线结构上的外部载荷列向量；t为时间。

在天线结构动力学分析过程中，由于结构自由度较多，通常采用模态叠加法将结构振动方程转换到模态坐标中进行分析。节点位移可以描述为各阶振动模态的叠加，即采用模态坐标描述天线结构节点位移

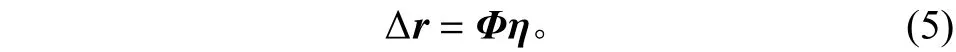
其中：Ф为由各阶模态列向量构成的模态矩阵；η为相应的模态坐标。

将式(5)代入式(1)可以得到天线主轴方向系数与模态坐标的近似关系式

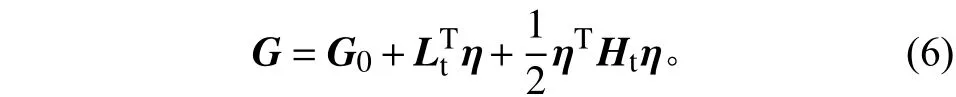
其中：Lt=ΦTL，为天线主轴方向系数对模态坐标的导数列向量；Ht=ΦTHΦ，为天线主轴方向系数对模态坐标的二阶Hessian阵。

至此，建立了网状反射面天线电性能与结构模态坐标的关系式。

1.2 工程建模分析方法

在工程实现过程中，可以借助天线电性能分析软件求解一阶导数向量Lt与二阶导数阵Ht，具体方法如下：

1）确定式(6)中的常量矩阵G0：通过工程软件，按照未发生变形的反射面天线计算得到天线辐射场强。

2）确定式(6)中的常量Lt、Ht：针对天线第i阶频率变形，选择合适的模态坐标振幅变形，按照前述静态分析的方法，计算得到多个不同模态坐标变形情况下的静态天线辐射场方程组，模态坐标趋近于0时，可确定因子Lt、Ht的极限常值。

3）获取天线、太阳电池阵等的柔性振动对整星柔性耦合系数矩阵[10-11]，建立天线在轨振动与电性能集成模型：

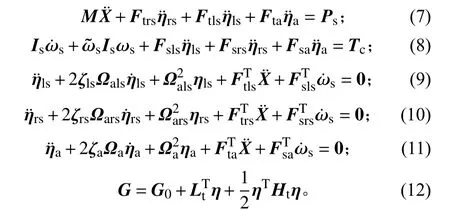
至此，建立了天线在轨振动与电性能集成模型，可以在此基础上进行反射面天线在轨工作工程中结构振动对电性能影响的分析。

2 仿真分析

2.1 反射面天线模态分析

以简单圆抛物反射面模型为例，基于本文方法计算时域振动过程中天线的电性能表现。反射面天线有限元模型如图1所示。模型划分采用三角形网格，固定约束反射面底部，对其展开固定边界下的模态分析，模态频率见表1，主要模态振型如图2所示。

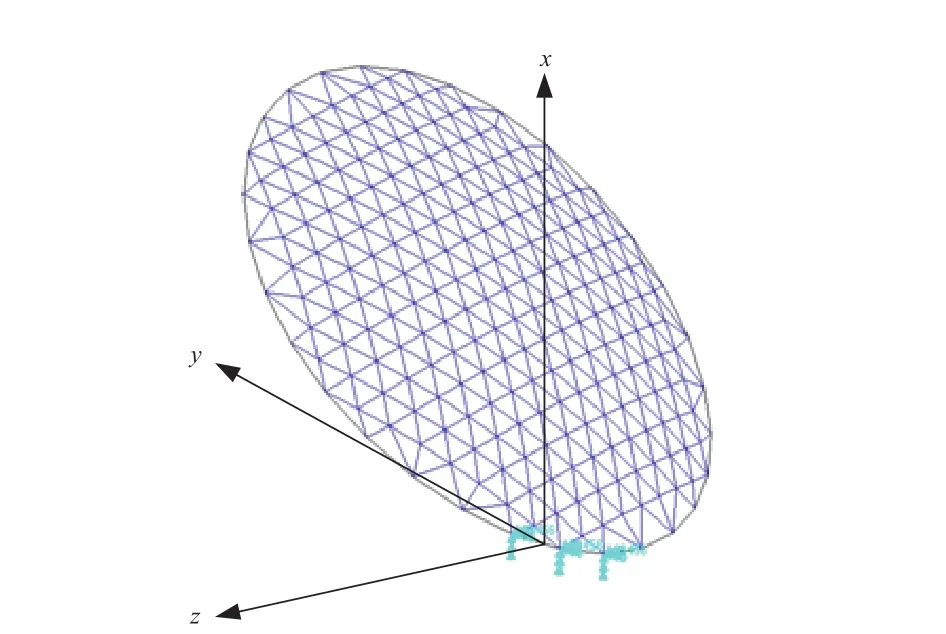
图1 反射面天线有限元模型Fig. 1 The FEM model of a reflector antenna

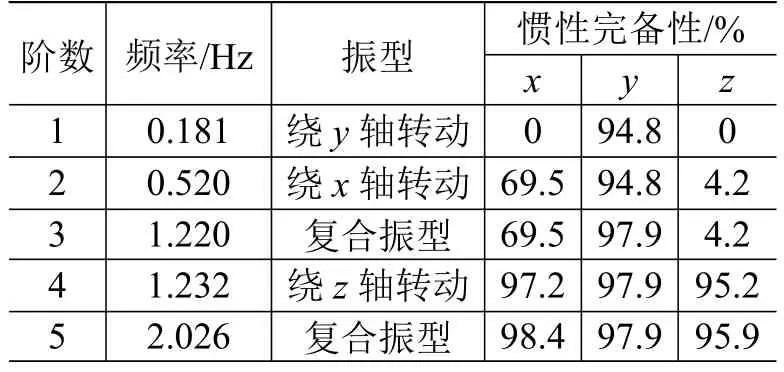
表1 反射面各阶振动频率Table 1 The vibration frequency of the reflector

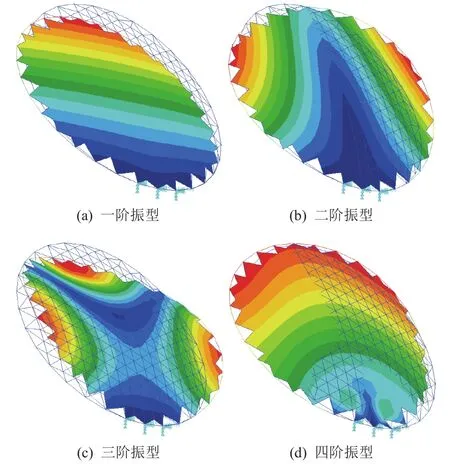
图2 天线反射面主要模态振型Fig. 2 The vibration modes of the reflector

对天线增益进行一阶展开，分析本文提出方法的对比情况。首先，根据结构动力学对系统的振动变形作模态空间离散

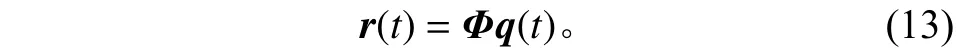
式中：r(t)表示天线所有节点在t时刻的变形量；Φ表示振型矩阵；q(t)表示t时刻的模态坐标。式(13)的展开形式为

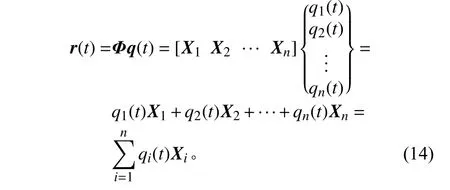
其中Xi表示第i阶模态的主振型向量。

由系统的惯性完备性准则可见，反射面天线振动前4阶的惯性完备性已经达到95%，因此仅考虑前4阶模态。

2.2 近似因子确定

在物理坐标下的任一时刻的位移 {r(t)}可以表示为4个主振型的线性组合，而线性组合系数就是模态坐标 {qi(t)}。那么按照第1章所述的方法，一阶近似表达式为

其中：gi为模态坐标qi对应的变形反射面产生的增益；g-i为模态坐标-qi对应的变形反射面产生的增益。lti因子的计算方法有3种：

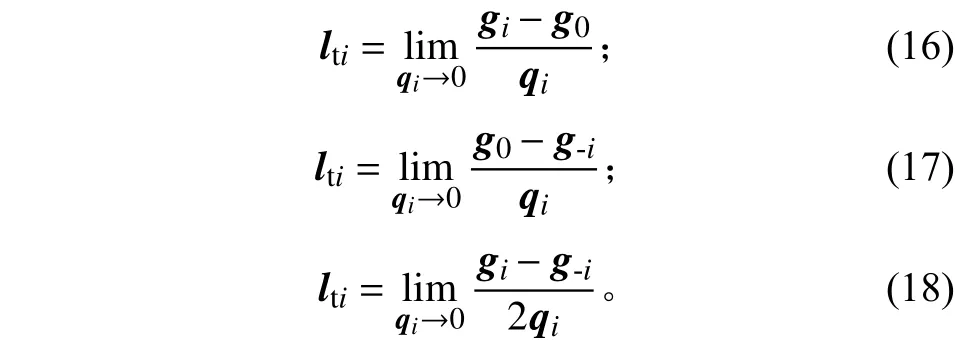
当qi→0达到一定程度时，式(16)～(18)将同时趋近于一常值，此时即认为得到了对应模态坐标qi量级的较精确的因子lti。

首先，求解未发生变形的反射面增益情况（见图3）[12]。

然后，按照表达式(15)依次减小模态坐标，对比一阶因子lti的变化情况（图4）可见，当模态坐标取0.01时，近似式的一阶因子lti趋近常值，认为此时的lti精度足够。

当模态坐标振动变形时，对比此物理变形下直接求得的增益情况与近似分析方法得到的增益情况。随机选取2组模态坐标(0.042, 0.016, 0.063,0.037)与 (-0.012, 0.006, -0.073, 0.006)，给出未变形的反射面、近似方法计算与直接使用软件计算得到的天线方向图对比情况（图5）。由图可见，采用近似方法可以得到增益主方向的偏差情况。那么，通过计算得到时变的模态坐标，则可以由近似方法得到时域内变化的天线主方向增益情况。此外，也可由一阶因子lti的量级分析影响天线增益的主要模态。

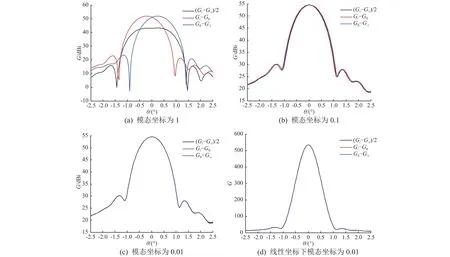
图4 不同模态坐标下的一阶因子变化Fig. 4 The first modal factor in different modal coordinates

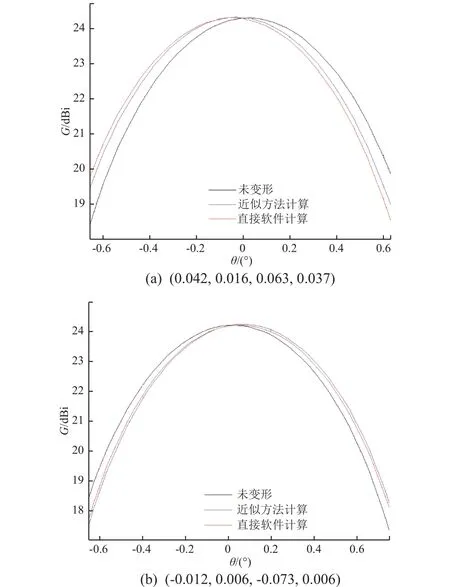
图5 天线方向图对比Fig. 5 A comparision of modal coordinates

2.3 在轨振动过程仿真分析

采用本文方法对某卫星开展振动载荷对电性能影响分析，并与传统分析方法进行对比。建立卫星有限元模型如图6所示。对整星开展自由状态模态分析，获得模态频率及振型如表2所示。

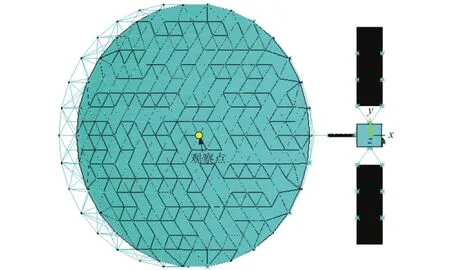
图6 整星有限元模型示意图Fig. 6 The FEM model of the satellite

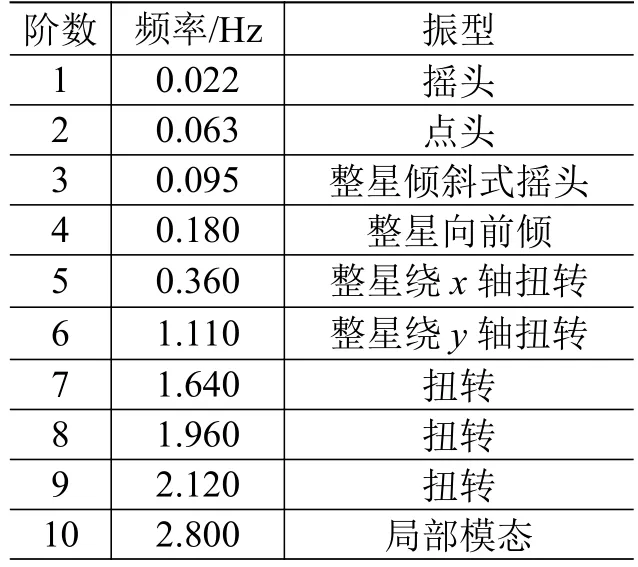
表2 天线各阶模态频率和振型Table 2 The vibration frequencies of the reflector

获取天线在轨激励下振动100 s的数据，因为主要关注天线薄膜面的振动情况，所以选取反射面中心点为观察点。获得100 s内观察点的振动情况如图7所示，其傅里叶变换曲线如图8所示。由图8可见，x方向振动主要响应位于0.06 Hz和0.17 Hz处，分别与天线的二阶和四阶固有频率吻合；y方向振动主要响应位于0.02 Hz处，与天线的一阶固有频率吻合；z方向振动主要响应位于0.02 Hz和0.06 Hz处，分别与天线的一阶和二阶固有频率吻合。因此，影响天线振动变形的主要是一阶、二阶、四阶模态振动。

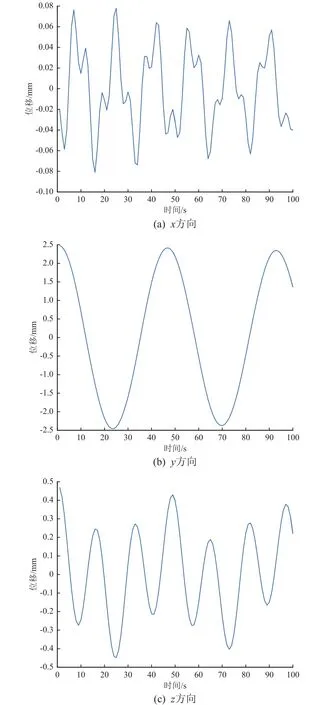
图7 天线反射面中心点变形Fig. 7 The vibration of the center of the reflector

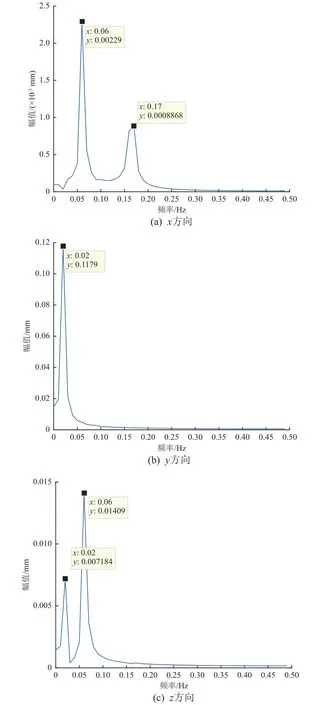
图8 天线反射面中心点变形的频率分析Fig. 8 The FFT for vibration of the center of the reflector

由本文所提分析方法可知，模态坐标是连接天线结构动力学与电性能的桥梁。各时刻模态坐标变化如图9所示。因其他阶模态坐标基本为0，所以此处只绘制了主要的一阶、二阶、七阶模态坐标变化图。

最后用本方法求出天线的主轴方向系数随时间变化曲线，并且与GRASP软件计算结果进行对比（见图10），发现两者差异较小。对此方向系数进行傅里叶变换（见图11），可见此时的结论与前面振动变形分析一致，一阶、二阶、四阶模态对于天线主轴方向系数的影响是主要的。

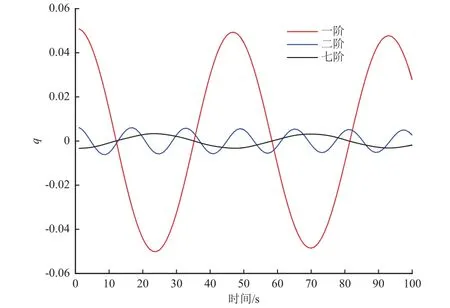
图9 主要模态坐标变化Fig. 9 The main modal coordinates

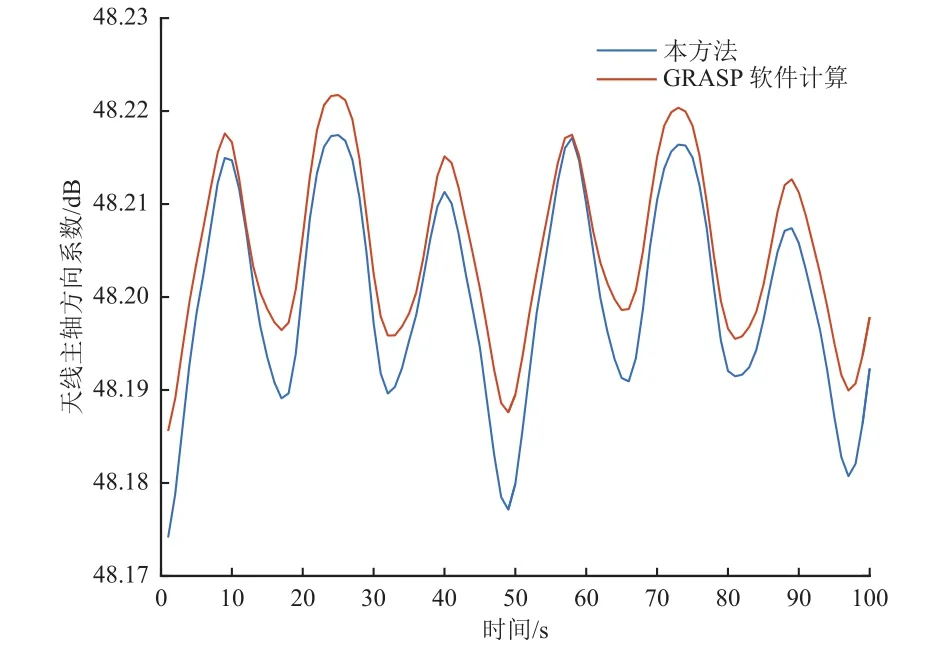
图10 本方法与GRASP软件计算所得天线主轴方向系数（时域）对比Fig. 10 The directivity obtained by our method as compared with that obtained with GRASP

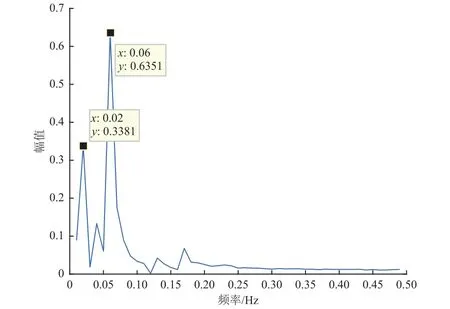
图11 天线的主轴方向系数（频域）Fig. 11 The FFT for the directivity

3 总结与展望

本文给出了一种反射面天线结构振动与电性能集成建模方法，针对带反射面天线卫星在轨情况建立动力学−控制−天线电性能集成模型，并结合反射面天线模型进行了计算应用。分析结果表明：本文方法能够给出从结构振动到天线电性能指向的直接近似关系式，进而得到振动过程中反射面天线的电性能变化情况，可用于分析天线在轨振动过程的电性能情况以及影响电性能的主要振动模态，弥补了当前电性能分析仅可针对单次静态结构变形展开的不足。研究同时发现，静态分析精度将决定近似因子的精度，并直接影响振动过程中天线电性能分析的精度。

此外，后续需进一步开展的研究工作包括：

1）应用静态分析方法对比验证模态空间近似展开法的误差情况；

2）确定模态空间展开式阶数，研究高阶数近似式的工程实现方法。