极化码的原理及分析

［］

1 引言

信道编码技术是无线通信物理层的最核心的基础技术之一，它的主要目的是使数字信号进行可靠的传递。信道编码技术通过在发送信息序列上增加额外的校验比特，并在接收端采用译码技术对传输过程中产生的差错进行纠正，从而实现发送信息序列的正确接收。为了实现可靠的信号传输，编码学家在过去的半个多世纪提出多种纠错码技术如RS码、卷积码，Turbo码等，并在各种通信系统中取得了广泛的应用[1]。我们知道LDPC是码长足够长时，是逼近香农极限的。香农极限即香农第二定理通俗来说就是，在码长R不大于信道容量C的情况下，存在一种能够实现信息的绝对可靠传输的编码方案。而所谓香农限就是同时满足绝对可靠、R逼近C的理想情况。香农第二定理并没有告诉我们如何进行信道编码，但是它指导着我们去寻找更加符合这种理想状态的编码方案，从turbo码到LDPC码，越来越逼近这一理想，而极化码的出现，在理论上实现了这一理想。2008年在国际信息论ISIT会议上，Arikan首次提出了信道极化的概念[2]，这种理想的编码方案使我们能够在一个噪声信道中以理论上最小的差错率和最快的速度进行信息传输。极化码的编码长度设计都是2的N次方，而目前航天器与地面计算机系统都是32位的比特计算与存储，所以极化码的特性也适合应用于未来的卫星领域。Polar码具有明确而简单的编码及译码算法。该编码因为拥有结构简单，译码复杂度低，而被国际移动通信标准化组织3GPP确定为5G eMBB(增强移动宽带)场景的信道编码技术方案，其中，Polar码作为控制信道的编码方案。本文将对极化码的原理进行阐述，研究其在二进制信道下码长，信道索引和信道极化现象的关系，并对连续删除SC译码基于matlab下进行了仿真实现，同时引入LDPC码中BP译码和最小和BP译码，将这三种译码方式进行了仿真对比。

2 信道极化

2.1 信道的参数与符号

极化码是基于二进制GF（2）构造的，其中Px表示X的概率分布，Px,y表示联合概率分布。表示行向量；表示由N个合成信道；表示将分解成N个子信道第i个子信道；信道转移概率W(y|x)[3-4]。定义在二进制DMC下信道容量和巴氏参数分别为I（W）和Z(W):

I(W)表示无错误传输的最大信息速率，Z(W)表示信道的可靠性。

2.2 信道的组合

信道组合就是将二进制DMC信道递归操作组合起来形成WN,其中N=2n，n>=0。

当n=0时，信道复制一次，有W1=W。当n=1时，信道进行组合得到信道W2，如图1所示：

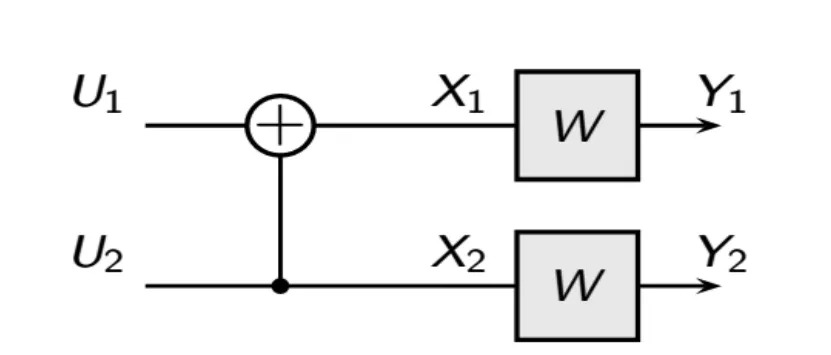
图1 W2的信道组合

当n=2时，信道进行组合得到W4,如图2所示：

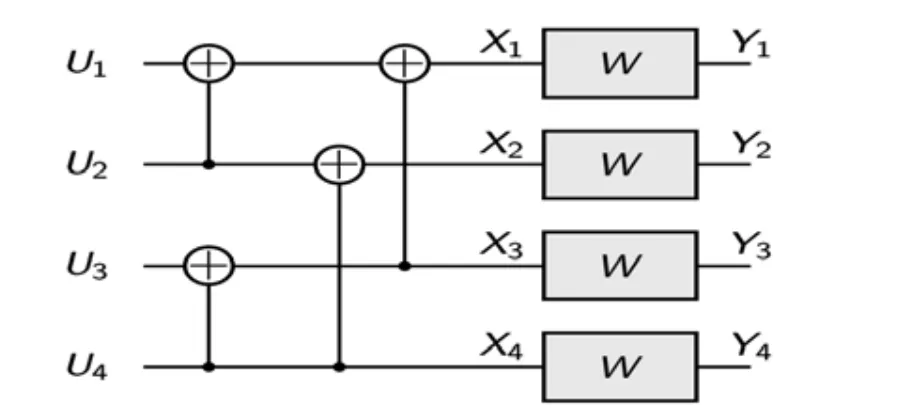
图2 W4的信道组合

当n=3时，信道进行组合得到W8，如图3所示：

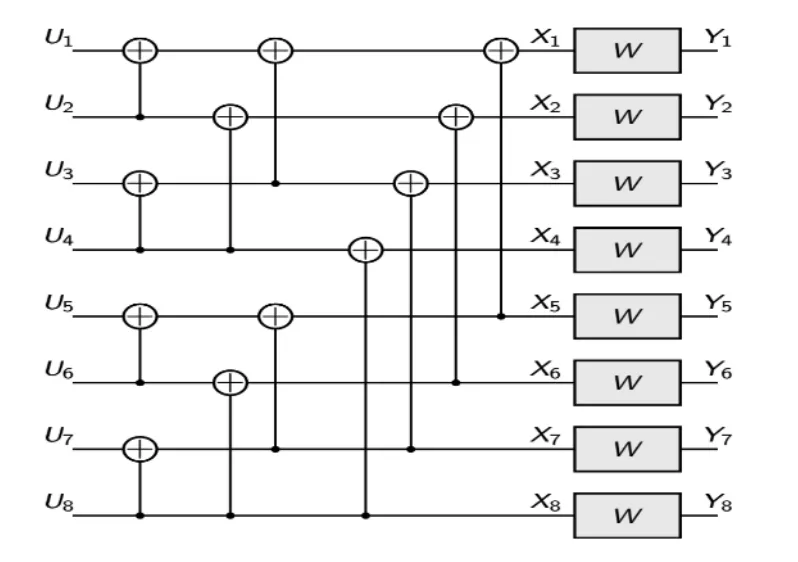
图3 W8的信道组合示意图

以此类推可以得到n=n-1时，组合信道WN,如图4所示：

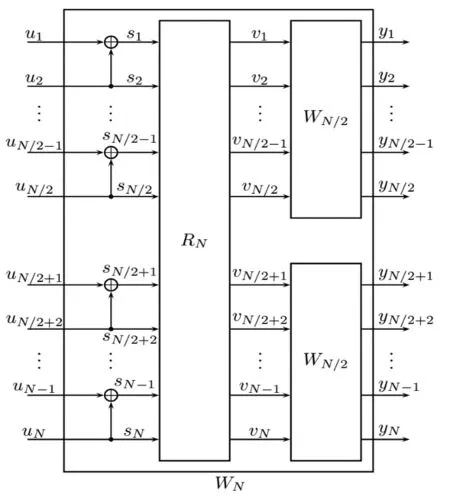
图4 WN的信道组合示意图

对输入序列u进行线性变换后可得到编码序列x，其变换过程可用生成矩阵GN来表示

此时其信道的转移概率为：

2.3 信道分裂

信道分裂是信道组合的逆过程，将合成信道WN再分解成N个二进制输入信道，其对应的转换概率为：

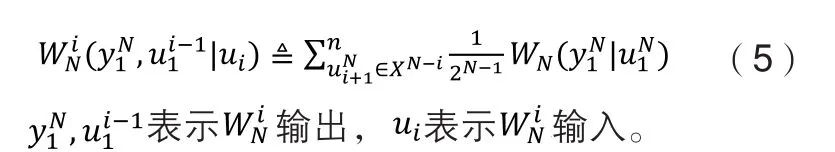
2.4 信道极化

信道极化是信道合并与信道分裂两种信道操作的结果[4]。在上述两种操作下，原本相同的N个W信道产生了极化现象，其中一部分信道容量趋于1，另一部分信道容量趋于0。

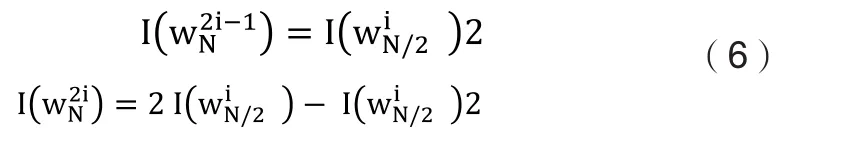
从图可以看出当删除概率为0.5时，随着编码长度N的增加，信道极化形象越加明显，图中所有点呈中心对称，当信道索引号很小时，对称信道容量趋近0；当信道索引号很大时，对称信道容量趋近于1。

由柱状统计图（6）中可以看出，当N比较小时，趋于0或1的个数占总个数比例不高，当N=32768时，信道容量0和1的数目比例都分别占到了大约49%。这就是信道极化现象。

3 极化码的原理

3.1 极化码编码

首先声明定义Kronecker(克罗内克积)：

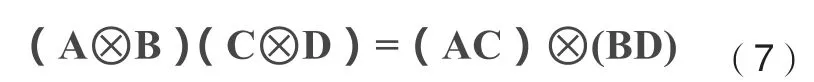
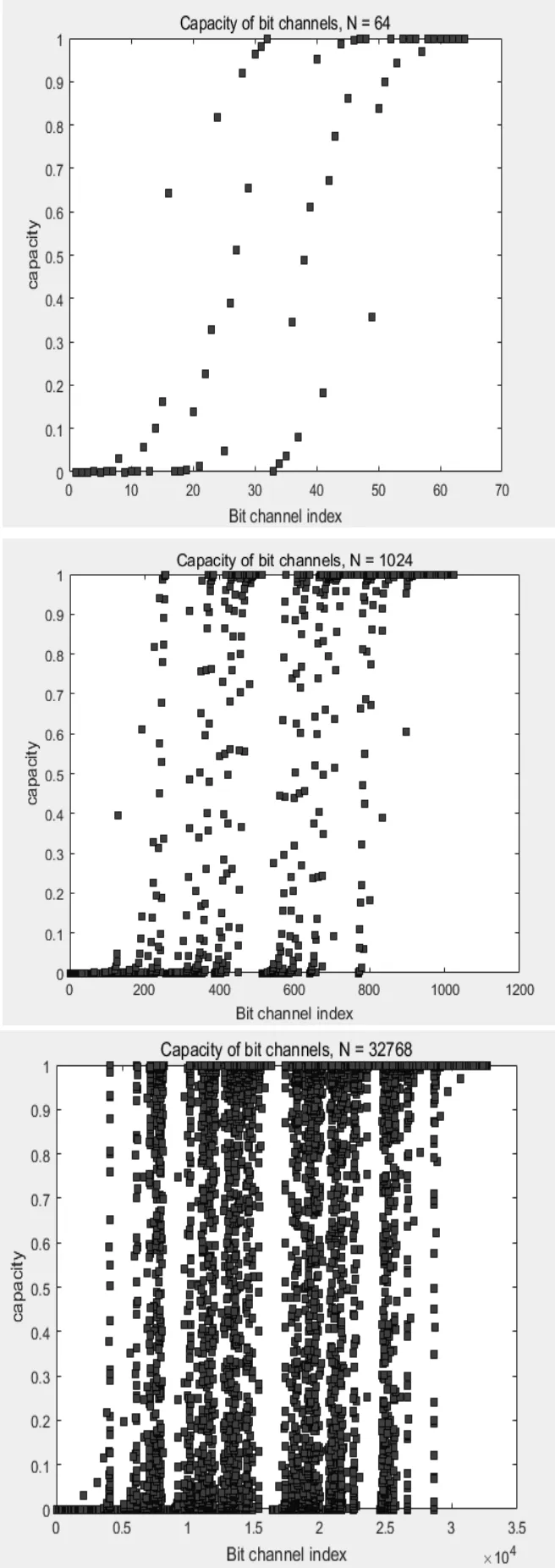
图5 N=64，1024，32768时的信道容量

将式（8）带入，可得：

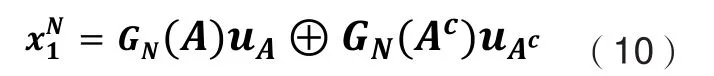
3.2 SC译码

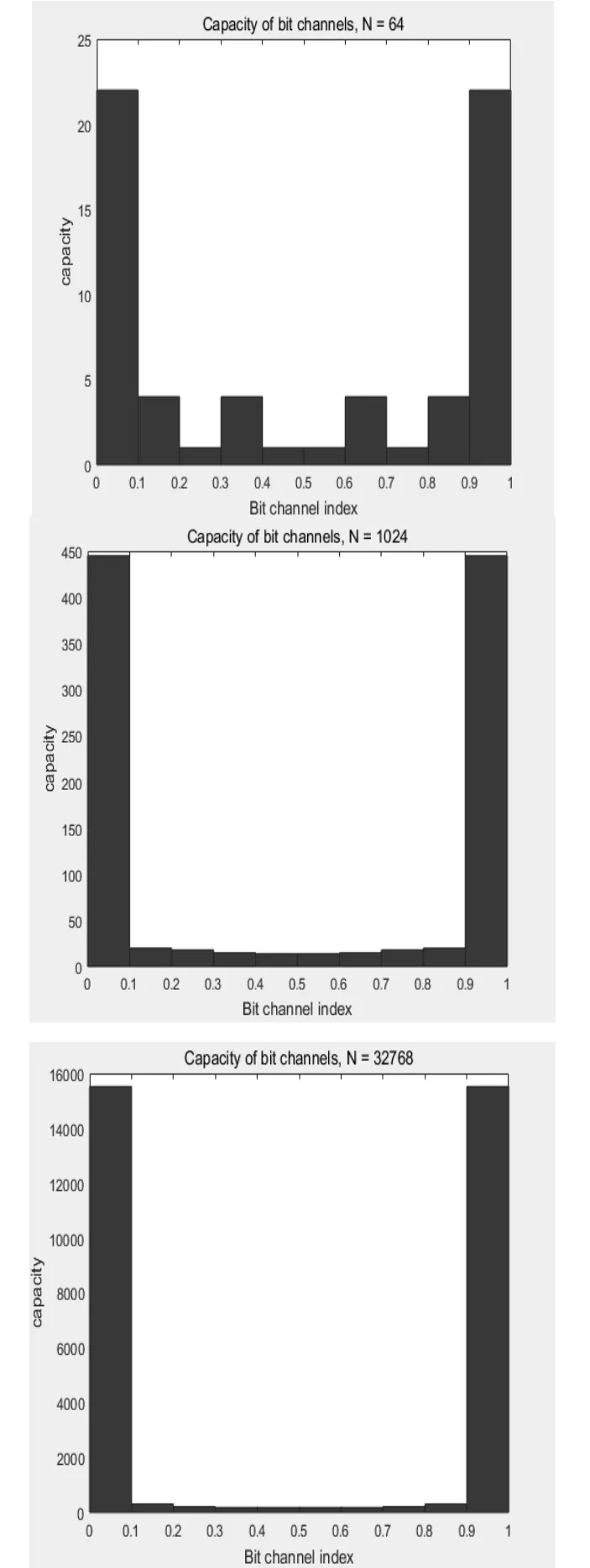
图6 信道极化现象的柱状统计图

设定第i个信息比特ui对应分裂信道为，通过该信道发出的信息，在接收端宜采用软判决译码，计算对数似然比：

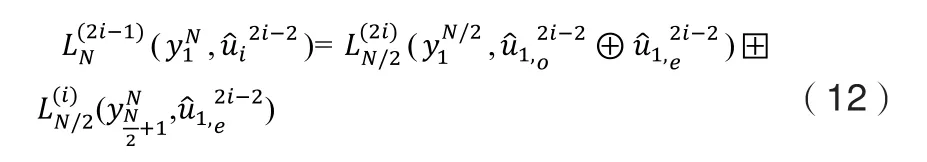
从上面推导过程中可以看出似然值的复杂度为N（1+logN）。

3.3 BP 译码

极化码生成矩阵可以 用因子图来表示，这样就可以使用BP译码算法对其进行译码【6,7,8】。BP译码就是通过节点之间相互传递信息，每个节点的更新公式如下：

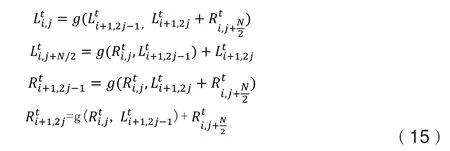
其中g(x,y)=ln((1+xy)/(x+y))，从信源端发出的信息,与信息集和固定比特值选取有关：

最后一层信道端的信息，接收到的信息设置为：

达到最大迭代值时，停止迭代，并做出判决：

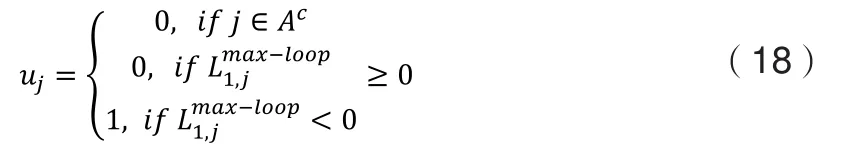
由以上译码过程可以看出，极化码的BP译码算法作为一种并行的译码算法具有不错的译码性能。

3.4 最小和BP译码

虽然BP译码具有不错的性能，但在LDPC码中我们可知其复杂度还是相对较高，因此，我们引入BP译码的改进方式，最小和BP译码。其译码时的节点更新公式依旧如式（15）一样。只是令其中g(x,y)=sign(x)sign(y)min(|x|,|y|),当y时，sign(y)=0,否则sign(y)=1。其译码算法迭代过程如下：

输入：接收矢量y;

迭代更新：对式15进行迭代更新每个节点先从右向左进行更新，到达最左侧后再从左向右进行更新，到达迭代最大值时停止更新。

最小和BP译码与BP译码方式最大的区别，在于判决处，BP的判决条件是否则。

4 仿真结果分析

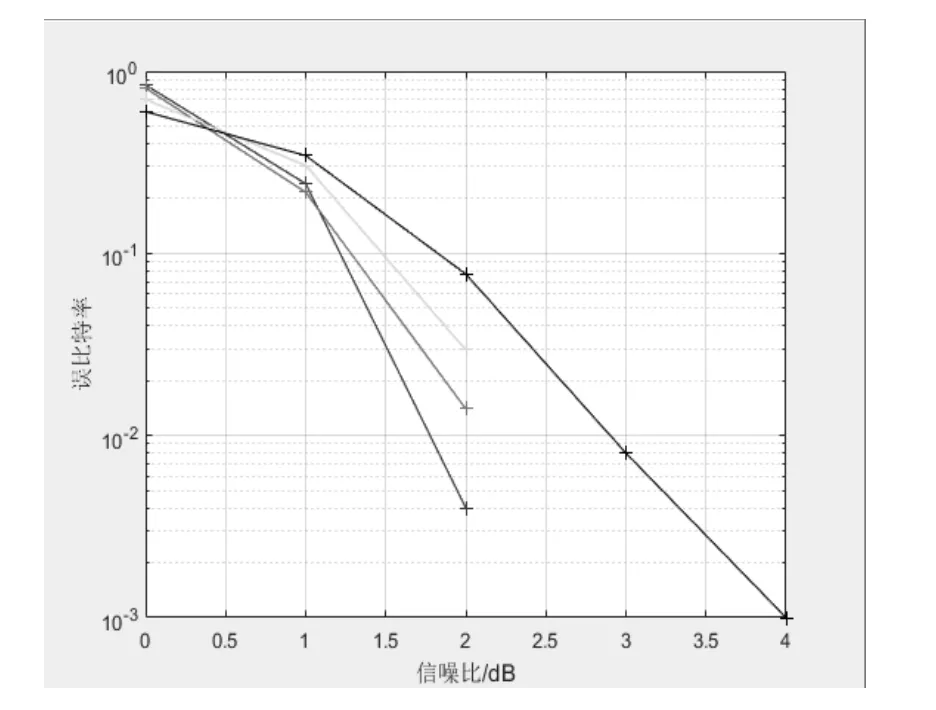
图7 不同码长下极化码的性能

在AWNG信道下，选取码率为0.25，采用SC译码方式，分别选取不同码长的极化码，在matlab下对其进行仿真，得到图4.7.其中黑色的为码长256，绿色为码长512，红色为码长1024，蓝色为码长2048.从图中可以看出，码长越长性能越好。随着SNR的逐渐增加，越加明显。这是因为码长越长，有前面信道极化仿真可知，信道极化越加明显，无躁信道的个数和比例都会显著提高，所以性能就越加好。

在AWNG信道下，选取码长为512，采用SC译码方式，分别选取不同码率的极化码，在matlab下对其进行仿真，得到图4.8.其中绿色为码率0.25，黑色为码率为0.5，红色为码率0.75。从图中可以看出，码率越小，极化码的性能就越好，说明编码效率直接影响码字的好坏。因为码率越低，信道编码对信道信息增加的冗余就越多，使得信息受到的保护就越多，因而性能就越好。所以编码速率不同时，发送的信息越多性能越差，因为信道极化，其中一部分信道是完美的无噪信道，当发送的信息多于好的信道个数时，就会导致其余部分信息在完全噪声信道下发送，最终出现这种情况。所以，信息位的选择很大程度上也与编码速率有关，码率越高，有效性越高，但可靠性就低；码率越低，有效性就低，但信息传输可靠性就高。

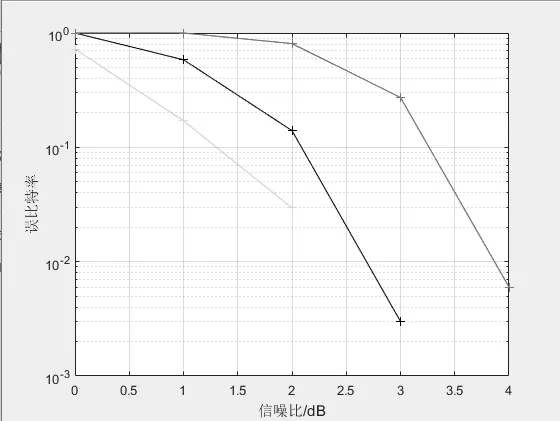
图8 不同码率下极化码的性能

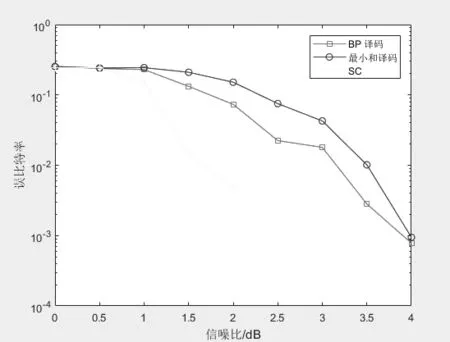
图9 不同码长下极化码的性能

在AWNG信道下，对极化码采取不同译码方式，将LDPC码中的BP译码和最小和译码方式引入，分别对其仿真，得到如图4.9所示。在SNR约小于3.5时，SC译码性能好于两种BP译码方式。当SNR大于3.5时，两种BP译码性能优于SC译码。而BP译码性能始终优于最小和BP译码方式。因为SC译码是一种串行译码，而BP译码方式是一种并行译码方式，在码长较大时，BP性能会优越一些。但BP译码一般在硬件上实现比较复杂，所以一般都用最小和BP译码来近似，虽然降低了BP复杂度，但译码性能却打了折扣。

5 总结

从代数编码和概率编码的角度来说，极化码具备了两者各自的特点。首先，只要给定编码长度，极化码的编译码结构就唯一确定了，而且可以通过生成矩阵的形式完成编码过程，这一点和代数编码的常见思维是一致的。其次，极化码在设计时并没有考虑最小距离特性，而是利用了信道联合（Channel Combination）与信道分裂（Channel Splitting）的过程来选择具体的编码方案，而且在译码时也是采用概率算法，这一点比较符合概率编码的思想。

SC译码算法以LLR为判决准则，对每一个比特进行硬判决，按比特序号从小到大的顺序依次判决译码。当码长趋近于无穷时，由于各个分裂信道接近完全极化（其信道容量或者为0或者为1）， 个消息比特都会获得正确的译码结果，可以在理论上使得极化码达到信道的对称容量,而且SC译码器的复杂度仅为O(NlogN)和码长呈近似线性的关系。然而，在有限码长下，由于信道极化并不完全，依然会存在一些消息比特无法被正确译码。当前面i-1个消息比特的译码中发生错误之后，由于SC译码器在对后面的消息比特译码时需要用到之前的消息比特的估计值，这就会导致较为严重的错误传递。因此，对于有限码长的极化码，采用SC译码器往往不能达到理想的性能。

为进一步提高有限码长极化码的性能，相继也提出了很多其它译码算法，SCL译码，CRC辅助SCL译码。通过多保留候选路径筛选来保证译码的正确性，但相对SC译码，其复杂度会提高很多，消耗更多存储空间。基于并行译码的置信传播（BP）译码，在低时延条件下可以获得比SC更好的性能。

极化码想要得到更多应用还要克服高速率通信下的时延和吞吐率问题，这是polar codes应用上最大的问题。