琴键堰水力特性数值模拟
2019-04-24侯冬梅
胡 晗,杨 伟,侯冬梅
(长江科学院水力学研究所,武汉 430010)
1 研究背景
近年来,由于气候变化导致极端洪涝灾害频发,加之社会经济的快速发展,水利工程的泄洪及防洪安全日益成为广泛关注的重要课题。许多国家,包括国际大坝委员会都在制定新的洪水标准,普遍将原来大坝的洪水标准提高1到2个量级,除了传统的最大可能洪水(MPF)外,甚至还要考虑极端致灾因子如溃坝等的影响,这就使得许多已建工程普遍存在泄洪能力严重不足的问题。因此,寻找一种高效、安全、经济,既可用于新建工程,又可用于已建工程提升改造的泄流设施就成为一个非常迫切的课题。
溢洪道是水库中用来泄洪、控制水库水位的建筑物。在洪水发生时,为了保障水库安全,溢洪道需要拥有较强的泄流能力,许多水利工程选用自由出流式的溢洪道,而不是闸门控制式的溢洪道。溢流堰通常可以分为直线型、曲线型和折叠型。在折叠型的溢流堰中,迷宫堰通过在固定宽度的情况下提供更长的溢流前缘总长,从而达到增强泄流能力的目的。迷宫堰可以建造为不同的形式,其中采用对称梯形设计的迷宫堰泄流能力要高于矩形设计的泄流能力。
琴键堰作为迷宫堰的一种全新形式,平面形状和传统迷宫堰类似,但采用向上游和下游悬出的结构(如图1)。相比于传统迷宫堰,琴键堰得益于向上下游悬出的结构,从而得到更小的生根面积。对大多数水库溢洪道来说,受地形等因素限制,单纯加宽溢洪道提高泄量一般很难办到,也不经济。而琴键堰能在较小水头下显著提升泄流能力,且改造容易实施,因此被认为是目前水库大坝溢洪道升级改造最有效的办法,在病险水库的除险加固方面有着广阔的应用前景。

图1 琴键堰Fig.1 Piano key weirs
在进行前期的试验之后,Lempérière和 Ouamane[1]对琴键堰作了如下定义:堰的结构为矩形,和钢琴的琴键类似;进水宫室和出水宫室底部分别向下游和上游倾斜;采用向上下游悬出的结构。图1为法国电力公司建造的琴键堰。
世界上第1个琴键堰建造于法国的Goulours大坝[2],鉴于其良好的实际效果,接下来陆续建造于St.Marc和Gloriettes大坝[3]。目前世界上已经新建了多座琴键堰溢洪道,有法国的Etroit(2009)、Gloriettes(2010)、Escouloubre(2011)、Malarce(2012),瑞士的Emmenau(2012),英国的Black Esk(2013),越南的 Van Pongh dam(2011),斯里兰卡的 Giritale(2013)等大坝[4]。目前在中国存在大量窄河谷、大泄流量要求的水利工程,在面对超标洪水时存在较大风险,迫切需要琴键堰这样能显著提高溢洪道泄流能力的工程手段,但国内尚无琴键堰的工程应用案例,因此其极具研究价值和应用前景。
近十几年来,围绕琴键堰的各个方面进行了广泛的研究。其中,Machiels等[5]通过模型试验研究了矩形琴键堰过流时的流态特征;Marcelo等[6]研究了琴键堰的水力设计;Karaeren和 Bozku[7],Anderson和Tullis[8]将琴键堰和迷宫堰进行了比较,认为琴键堰更有优势。中国水利水电科学研究院(以下简称中国水科院)耿运生与孙双科[9]对这种琴键堰进行了基本的试验研究,2014年中国水科院的郭新蕾等[10]在搜集国外试验数据的基础上,给出了琴键堰泄流能力的一个拟合公式;2015年,李国栋等[11]通过数值模拟方法,研究了琴键堰不同溢流前缘泄流特性,获得了琴键堰出水口、进水口及侧向3个溢流前缘上的泄流量,分析了出水口、进水口及侧向泄流在总泄流中所占的比例及泄流效率随水头升高的变化规律。
琴键堰过流时,部分水流越过侧堰进入出水宫室,与出水宫室的水流发生碰撞,流场复杂,呈现出明显的三维特性。因此其流量计算无法直接套用经典的堰流流量计算公式。
多名研究者在琴键堰流量计算方面进行了探索。Leite等[12]通过定义琴键堰的流量比系数r来描述琴键堰的泄流能力。Abdorreza等[13]提供了琴键堰在自由出流和淹没出流工况下的流量系数。Machiels等[14]通过一系列的试验,研究了单个参数对琴键堰水力特性的影响。琴键堰的单宽流量被分为了3部分分别计算,有明确的物理意义。然而,公式中由于未考虑到进水宫室内的水头损失,其计算结果与 Lempérière的试验结果[1]相差较大。
在之前的研究与应用中,最初琴键堰的设计方法是基于现有的从缩小比例模型的理想化试验结果得出的,其主要几何参数由对比例模型的几何尺寸外推放大确定。根据这个几何形状,对缩小尺寸的模型进行测试,以确认它的效率。琴键堰的结构从最初的几何结构经过工程师们一步一步修改之后最终设计成形。直到目前,综合各方面因素进行的琴键堰优化设计工作还处在探索阶段,且尚无从机理上分析影响琴键堰的泄流效率的研究。本文作者筛选出了对琴键堰泄流效率产生显著影响的几何特征,并提出了物理意义明确且精度高的琴键堰流量计算方法,以期为琴键堰的设计提供可靠的依据。
2 琴键堰的结构
琴键堰的几何结构可以看作不同结构单元的结合:基本结构、护墙和上游端导流结构。进水宫室是一个琴键堰单元中开口朝向上游方向的“键”,由2个侧堰和下游端堰顶限定。出水宫室是一个琴键堰单元中开口朝向下游方向的“键”,由2个侧堰和上游堰顶限定。琴键堰的基本结构由若干个“琴键堰单元”组成。由给定的基本结构可以确定的参数有:溢流前缘总长度L、琴键堰总宽度W和琴键堰单元数目Nu。
琴键堰单元代表完整的最小琴键堰结构,由一个完整的进水宫室、2个侧堰和位于两侧各一半的出水宫室组成。为了使表达更直观,给琴键堰单元中进水宫室的各个参数定义下标“i”;出水宫室的各个参数定义下标“o”;侧堰的各个参数定义下标“s”。
定义琴键堰单元几何形状的结构参数有单位宽Wu,进/出水宫室宽度 Wi和 Wo,琴键堰堰高 P,进/出水宫室坡度Si和So,向上游和下游方向悬出结构的长度Bo和Bi,侧堰长度B。
由于琴键堰主要建于大坝坝顶,琴键堰以下大坝的高度定义为Pd。

图2 琴键堰结构Fig.2 Structure of piano key weir
Lempérière和 Ouamane[1]指出相对溢流前缘长度L/W是影响琴键堰泄流能力最主要的几何参数,该观点也被 Marcelo等[6]所证实。而 Lempérière指出,L/W的值等于5时,琴键堰的泄流能力和其工程造价能达到最佳的平衡。本文在系统研究其他几何参数造成的影响时,相对溢流前缘长度L/W的值取为由 Lempérière等[15]提出的最佳值“5”。
3 数值模拟方法及其验证
3.1 数学模型及边界条件
本文以Flow-3D软件为计算工具,选用VOF模型对琴键堰的三维流场进行模拟。其控制方程如下。
连续性方程:
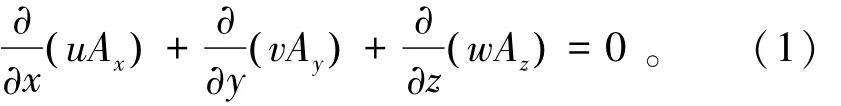
动量方程:

式中:u,v,w分别为 x,y,z方向的流速分量;Ax,Ay,Az分别为计算单元x,y,z3个方向上可流动的面积分数;t为时间;VF为各计算单元内液体的体积分数;ρ为液体密度;p为作用在流体微元上的压力;Gx,Gy,Gz分别为 x,y,z方向上的重力加速度;fx,fy,fz分别为x,y,z3个方向的黏滞力。选择标准k-ε模型封闭方程。
首先按照 Lempérière的试验[1]建立了相同尺寸的琴键堰数值模型,其几何参数如表1所示。在计算模型中的琴键堰上游方向设置了10 m的行进段,以确保琴键堰中水流的流态不会受到上游边界条件的影响。

表1 Lempérière琴键堰试验模型尺寸Table 1 Geometrical parameters of the piano key weir from Lempérière’s experiment
在设置计算网格时,垂直于固体表面的网格间距,为保证数值计算的精度,要求在贴近固体表面的层流中必须有至少一个计算网格节点。总体选择10 cm的均匀网格进行计算,网格形状为立方体,x=y=z,对关键的结构特征处进行网格加密处理。
进口边界条件设置为固定水面高度的边界条件;上部边界条件设置压力为0的压力边界条件;琴键堰结构的表面设置为无滑移的固体边界条件;在两侧,即进水宫室和出水宫室中间,采用对称边界条件。为了确保琴键堰中的流态区域达到稳定,每个数值模拟工况运行时间设置为30 s。
3.2 数学模型的验证
Lempérière等人提供了很大水头范围的单宽流量试验数据(表2),可以供本研究的数值计算结果进行对比。琴键堰的运行效率可以定义为,在给定上游水位的情况下,通过琴键堰排向下游的总单宽流量q,即单位堰宽的泄流量。
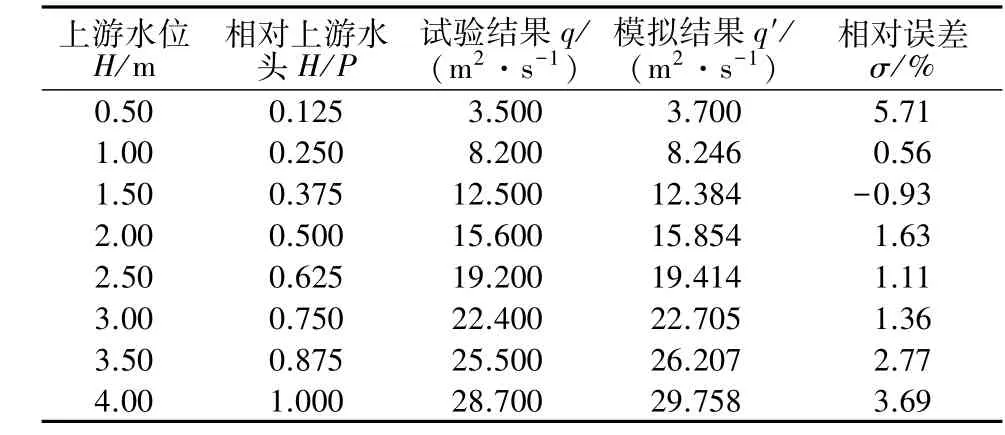
表2 数值计算误差分析Table 2 Comparison of specific discharge between physical and numerical model
与试验结果比较发现,数值计算结果平均相对误差为2.22%,最大相对误差为5.71%。证明采用VOF模型的计算结果是可靠的,能准确反映琴键堰内的流动特性。
4 溢流前缘流量分布
由于本研究采用数值模拟的方法,因此可以将流过琴键堰溢流前缘的流量分为几个部分,进行精细化分析。为了定量分析琴键堰溢流前缘各部位在不同上游水头工况下流量分布情况,本文用曲线坐标s来标识半个琴键堰单元的溢流前缘。
由于琴键堰为对称结构,半个单元的琴键堰中的流态就可代表整个琴键堰中的流态。本研究将半个单元的琴键堰的堰顶分为3段(见图3和图4):出水宫室上游端堰顶(AB)、侧堰(BC)和入水宫室下游端堰顶(CD)。这3部分堰顶的过流量之和即为半个琴键堰单元的总泄流量。

图3 琴键堰单元的堰顶划分Fig.3 Division of the crest of piano key weirs
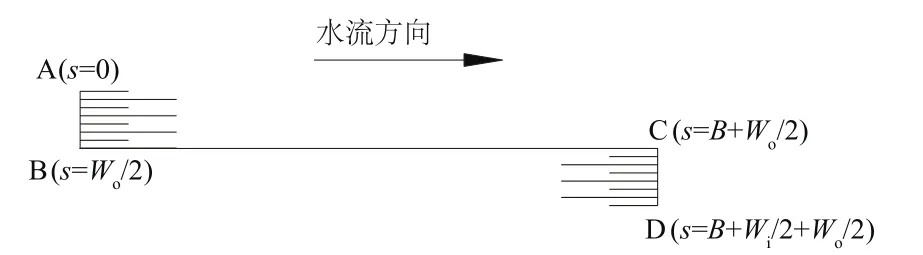
图4 曲线坐标s平面图Fig.4 Curvilinear abscissas
出水宫室上游端堰顶(AB)、侧堰(BC)和进水宫室下游端堰顶(CD)的过堰流量分别为

式中:u为出水宫室上游端堰顶(AB)上方垂直于上游堰顶的流速分量,同样垂直于进水宫室下游端堰顶(CD);v为侧堰(BC)上方垂直于侧堰的流速分量。
本研究对按照Lempérière的试验同尺寸的琴键堰数值模型在不同的上游水头工况进行了模拟。得出了不同上游水头工况下 (0.5,1.0,2.0,3.0,4.0 m),琴键堰溢流前缘各部位的单宽流量分布曲线,如图5所示。

图5 琴键堰溢流前缘各部位的单宽流量分布曲线Fig.5 Discharge per unit width at the crest of a piano key weir unit for various H values
图5 清楚地表明各流量工况下,出水宫室上游端堰顶(AB段)的过堰单宽流量分布均匀,并接近于同等水头下薄壁堰的单宽流量;由于受到侧堰和出水宫室上游端堰顶(AB段和BC段)过堰水流交汇影响,在出水宫室上游堰顶靠近侧堰处(B点附近)单宽流量显著减小;侧堰(BC段)过堰单宽流量小于出水宫室上游端堰顶(AB段),同样受到过堰水流交汇影响,而且靠近两端的部位(B点和C点附近)单宽流量显著减小;进水宫室下游端堰顶(CD段)的过堰单宽流量大小介于出水宫室上游端堰顶(AB段)和侧堰(BC段)之间,在进水宫室下游端堰顶靠近侧堰处(C点附近)单宽流量显著减小。
表3概括了琴键堰过堰总流量中溢流前缘各部位流量的占比。

表3 一个琴键堰单元中溢流前缘各部位单宽流量分布Table 3 Distribution of discharge per unit width along the crest of a piano key weir unit
从以上分析可以发现,在较低上游水头的工况下,琴键堰进水宫室内主流方向的流速较小,自由水面趋于水平,各部分堰顶的流态都接近于薄壁堰,琴键堰主要的泄流量由侧堰提供(在0.5 m水头工况下占总体流量的82.00%),此时琴键堰通过较大的相对溢流前缘长度L/W来提高泄流量的优势得以充分发挥。随着上游水头的提高,琴键堰上游端堰顶的流态由于不受其他因素干扰几乎保持不变。而侧堰过堰水流由于会受到进水宫室中主流流速和出水宫室另一侧过堰水流的正向干扰这2个因素的影响,导致侧堰过堰流量占比相对下降。琴键堰下游端堰顶的流量,由于进水宫室中不断增大的水头损失,其占比也相对下降。在4 m上游水头的高水头工况下侧堰流量只占整体泄流量的一半左右,因此琴键堰通过较大的相对溢流前缘长度L/W来提高泄流量的优势被大幅削弱。
5 流量计算方法
5.1 总流量分析
琴键堰的泄流能力定义为某一水头工况下的单宽流量,其表达式为

式中:Q为一个琴键堰单元的总流量;Wu为一个琴键堰单元的宽度。
一个琴键堰单元的总流量可以被看作由3部分构成:出水宫室上游端堰顶流量Qu、侧堰堰顶流量Qs和入水宫室下游端堰顶流量Qd,即

结合琴键堰的结构(图2),出水宫室上游端堰顶,侧堰堰顶和入水宫室下游端堰顶的平均单宽流量分别为

于是琴键堰在某一上游水头工况下的单宽流量为
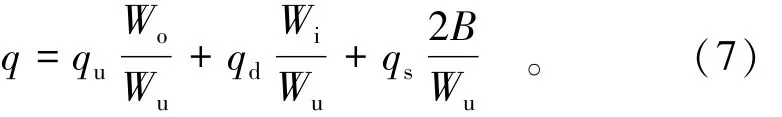
接下来本研究将分别讨论出水宫室上游端堰顶,入水宫室下游端堰顶和侧堰堰顶的平均单宽流量(qu,qd,qs)的计算方法。
qu,qd,qs的值都与上游水头H和琴键堰的结构参数相关。为了找出影响琴键堰堰顶各部分的单宽流量(qu,qd,qs)的主要影响因素,本研究采取了正交试验的研究方法。
在琴键堰中,对出水宫室上游端堰顶,入水宫室下游端堰顶和侧堰的平均单宽流量(qu,qd,qs)产生影响的因素一共有2方面:一方面是上游水头H;另一方面是琴键堰的结构参数,包括 Wu,Wi,Wo,P,B,Bo,Bi。这7个结构特征参数能够确定琴键堰单元的结构。
为了让研究更具一般性,本研究对琴键堰的结构参数和上游水头作了无量纲化处理。固定琴键堰单元宽度Wu=4.8 m,其他几个参数取为和琴键堰单元宽度的相对值。

式中Lu为1个琴键堰单元的溢流前缘总长。
在此条件下描述琴键堰结构参数和运行工况的一共有4个因素:相对堰高、进/出水宫室宽度比上/下游悬出长度比相对上游水头

表4 不同工况下的琴键堰结构参数Table 4 Geometric parameters of piano key weirs simulated under different conditions
本研究考虑以薄壁堰单宽流量的计算公式为基础来确定 qu,qd,qs的计算方法。
5.2 上游端堰顶流量
由于过堰水流存在相互干扰现象,因此在同样上游水头工况下,和普通向上游端倾斜的薄壁堰相比,琴键堰的上游端堰顶的流速在两端靠近侧堰主流方向的流速均有所减小。因此琴键堰上游端堰顶的单宽流量qu略小于薄壁堰在同样工况下的单宽流量qsharp-crested。
假设:
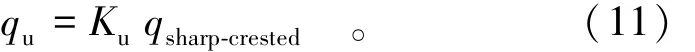
式中Ku为比例系数。
薄壁堰的流量计算公式为

其中,薄壁堰的流量系数Cs为
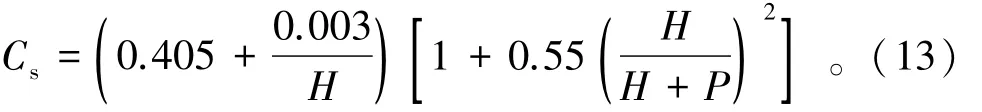
在这里为了计算堰高PT,必须考虑琴键堰下方的水坝高度Pd。则有

因此,

正交试验结果显示任意体型的琴键堰在不同水头工况下 qu/qsharp-crested的值都接近于常数 0.932。因此,有

5.3 下游端堰顶流量
由于总水头在进口处的局部损失和在进水宫室内的沿程损失,如果将琴键堰下游端堰顶看作一个向下游倾斜的薄壁堰,则在同样上游水头的工况下,琴键堰下游端堰顶单宽流量qd小于向下游方向倾斜的薄壁堰的单宽流量q′sharp-crested。
假设:

式中Kd为比例系数。
因此,

本研究采用由Boussinesq[16]提出的计算方法,来计算倾斜薄壁堰的单宽流量。即在薄壁堰的流量计算公式中加入坡度修正系数Ki。

式中i为薄壁堰的倾斜角度。
在琴键堰中Ki为
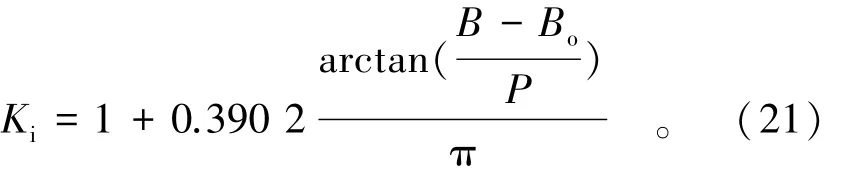
代入普通薄壁堰计算公式可得
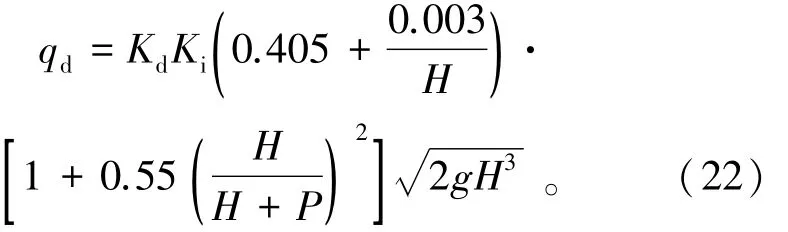
根据数值模拟结果可得知Kd是上游水头和琴键堰体型参数的函数。正交分析的结果显示的值只与相对堰高和相对上游水头著相关。
通过最小二乘法得出了Kd为

5.4 侧堰流量
同样假设:

式中:Ks为侧堰流速修正系数,用于考虑相对堰高和相对上游水头对侧堰单宽流量q产生的影响;KW为堰宽修正系数,用于考虑进/出水宫室宽度比对侧堰单宽流量q产生的影响。
代入普通薄壁堰计算公式可得

式中Pe为琴键堰侧堰的平均堰高。由琴键堰的结构可知

通过最小二乘法得出了Ks和KW的计算式为:
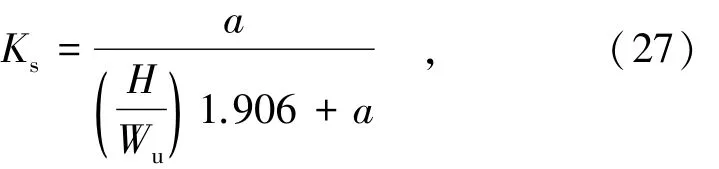
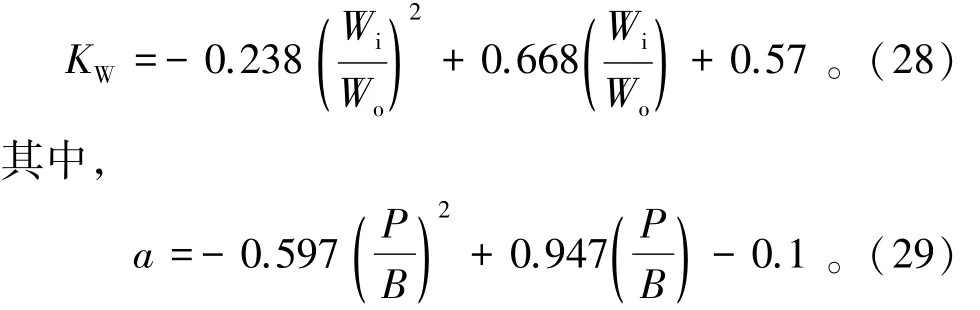
5.5 误差分析
为了验证式(7)的计算精度,本研究将式(7)的计算结果与Lempérière的试验成果进行了对比,并将Machiels公式和Kabiri-Samani公式的结果一同进行了对比,如图6所示。

图6 琴键堰单宽流量计算值与试验结果的对比Fig.6 Comparison between experimental and calculated discharge per unit width of piano key weir
在不同工况下用式(7)计算的最大相对误差为6.7%,平均相对误差为3.7%。而Kabiri-Samani公式的计算结果最大相对误差为23.6%,平均相对误差为11.9%;Machiels公式的计算结果最大相对误差为16.3%,平均相对误差为10.1%。因此,式(7)的计算结果能够满足设计参考和进行优化设计时的流量计算精度要求。
6 结 论
通过对不同几何结构的琴键堰进行的正交数值试验,确定了影响琴键堰泄流效率的主要几何参数对水力特性的影响:相对上游水头H/Wu对琴键堰上游端堰顶的单宽流量qu产生显著影响;相对堰高P/Wu和相对上游水头H/Wu对琴键堰下游端堰顶的单宽流量 qd产生显著影响;相对堰高 P/Wu、进/出水宫室宽度比 Wi/Wo和相对上游水头H/Wu对侧堰堰顶单宽流量qs产生显著影响。针对影响琴键堰泄流效率的主要几何参数,进行了数值仿真计算,基于水力学理论,推导了琴键堰的流量计算公式,并验证了流量计算公式的精度较高。
