梁动力分析的集中质量矩阵严格生成方法

高岱恒，郭宏伟，郑 宏

（1.北京工业大学建筑工程学院，北京 100124；2.中国科学院武汉岩土力学研究所，武汉 430071）

1 研究背景

梁作为工程结构中基本的构件，被广泛地应用于工程建设当中。对于梁结构的静力、动力学研究始终是土木工程领域的重点问题。

目前，对惯性特性的合适表述可以显著地降低计算开销并得到精度较高的结果。有许多学者对质量矩阵生成方式进行了卓有成效的研究［1-4］。有限元中，常用的2类质量矩阵为一致质量矩阵（CMM）和集中质量矩阵（DLMM）。

Archer［5-6］在使用一致质量矩阵进行动力学分析方面取得了非常好的成果。但使用一致质量矩阵的缺点很突出：①无论是用显式积分算法求结构瞬态反应还是对自由振动的广义特征值求解，采用一致质量矩阵的效率很低；②在接触问题和波的传播动力学中，采用一致质量矩阵时，求出的解会出现震荡现象。

基于此，在动力分析中，采用集中质量矩阵会是一个更好的选择。

然而，对于二维问题，以板单元为例，用广为采用的row-sum［7］方法形成的集中质量矩阵，其转角自由度对应的质量为0，这样会导致集中质量矩阵正定性丧失，从而无法直接用于Newmark法和子空间迭代法，这样不仅使实现变得困难，而且牺牲了很多数值特性。而HRZ方法［8］——对角缩放方法对任意单元（如三角形单元、八节点等参元等）都可以生成正定的集中质量矩阵，但是却没有严格的数学基础。尽管HRZ方法在结构力学、固体力学以及热传导等方面得到了成功的应用，但是由于其理论基础不严格，始终值得警惕。根据现有的实践表明，HRZ方法在流体计算中效果不佳。

本文基于数值流形方法（numerical manifold method，NMM），提出了一种基于严格数学理论的对角化集中质量矩阵的生成方法，并将其应用于梁动力分析中。

2 梁振动分析的有限元方法

2.1 梁振动的变分提法

本文采用均质等截面欧拉-伯努利（Euler-Bernoulli）梁来对结构进行分析。为了叙述上的方便，以简支梁为例，其受迫振动的变分提法为

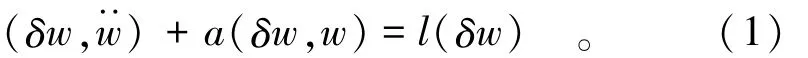
式中：（δw，w··）为惯性力所做的虚功；a（δw，w）为广义力做的虚功；l（δw）为分布荷载所做的虚功。展开形式为：

式中：w（x，t）为梁的横向位移；ρ为梁的密度；A为梁的截面面积；L为梁的长度；E为材料的弹性模量；I为梁的惯性矩；q（x，t）为分布荷载；x，t分别为沿梁轴方向的坐标和时间；δw中的δ表示变分符号。

2.2 空间离散

假设梁单元被离散成ne个单元和n个节点。对于每一个单元e，梁挠度的一阶Hermite插值形式为

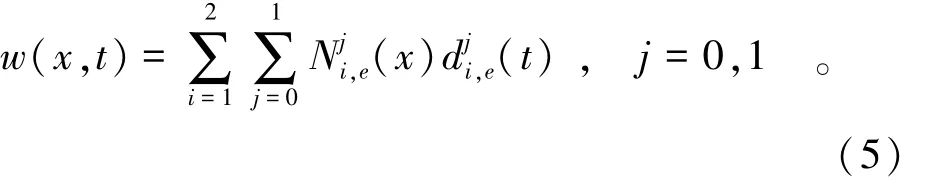
其中：

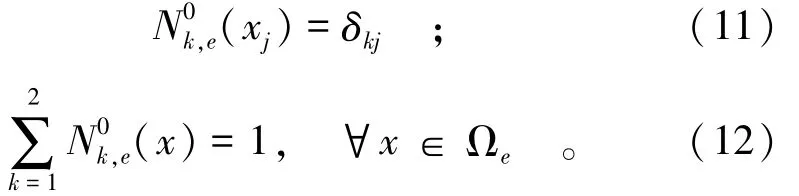
将式（6）代入式（1）中，可以得到半离散形式的微分方程组，即

式中：M为整体质量矩阵；K为整体刚度矩阵；f为整体载荷向量，都是由相应的单元矩阵组集而成；d为所有结点自由度组成的向量。

对于式（13）的求解，有2种普遍的方法：振型叠加法和对时间的直接积分法。按照计算每一时刻的动力反应是否需要求解耦联方程组，可以将直接积分法分为隐式算法和显式算法2类。当采用显式算法时，对自由度数目很大的情况，采用对角化集中质量矩阵，对节省计算资源开销和内存占用来说意义重大。此外，在一些场合还可消除解的伪震荡现象。

同样，当使用振型叠加法求解问题时，如果M为对角化矩阵时，可以将问题形式从广义特征值降为常义特征值，这同样降低了计算开销（因为质量矩阵是稀疏的）。相比使用一致质量矩阵，采用集中质量矩阵会更容易找出结构的更多高阶模态来进一步完善分析。

3 基于数值流形法（NMM）的集中质量矩阵生成

3.1 数值流形法（NMM）的提出

NMM是石根华博士［10］于1991年首次提出，它基于2套覆盖（数学覆盖和物理覆盖）和接触环路来建立。对于求解岩体的不连续变形和节理裂隙扩张的模拟等问题非常有效。

数学覆盖（Mathematical Cover）可以视为一系列数学片的集合，与有限元不同：数学覆盖通常大于实际结构的物理区域，物理覆盖（Physical Cover）是物理区域内所有物理片的集合。物理片是由物理区域上如边界、裂缝等不连续面切分数学片后得到的，其中每个物理片都定义一个权函数［11］和相应的局部逼近。

数值流形法是一种可以统一处理连续问题和非连续问题的计算方法，目前在岩土工程中大量使用，将来有望在更广阔的领域得到应用。

3.2 集中质量矩阵生成

本方法的理论［12-13］是一种关于高阶等参元的对角质量矩阵的生成方法，但是，用于四阶问题所采用的Hermite插值并不在单位分解框架内，所以在应用文献［12］的方法之前，需要从Hermite插值中取出片上的权函数及其局部逼近。

为此，先从NMM的角度出发，审视梁问题的有限元法。

由图1可知，梁由3个梁单元组成。这里，物理片1、物理片2、物理片3、物理片4可以用点1，2，3，4来表示，这4个点都是拓扑星点。

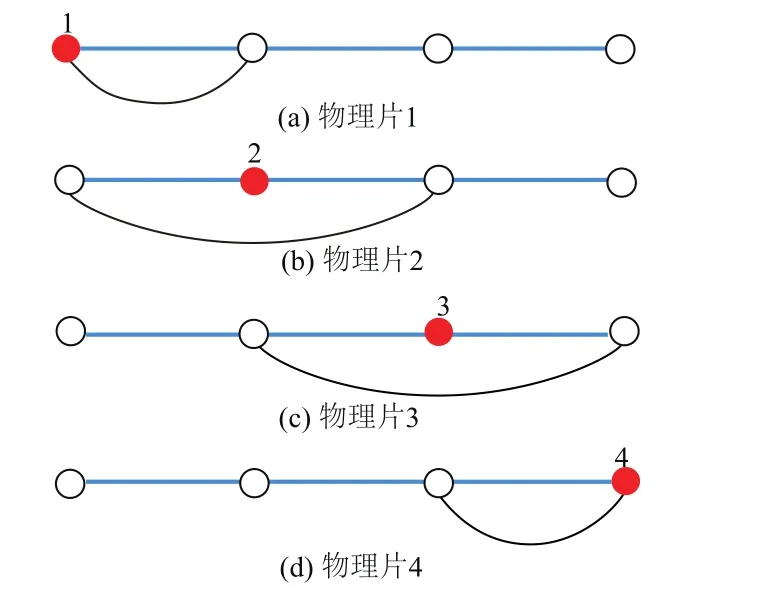
图1 结构物理覆盖Fig．1 Physical cover of structure

在本文这个特例中，流形单元即为普通单元，是该单元的2个节点所对应的物理片的公共部分。即：流形单元1为物理片1和物理片2的共同部分，流形单元2和3同样为对应物理片共同部分。流形单元1和2的形成如图2所示。

图2 流形单元的形成Fig．2 Formation of manifold elements

本文3.1节中提到了每个物理片都有对应的权函数，取物理片上2个单元的Hermite插值的零阶插值函数来组成权函数是很自然的选择。图3为各个物理片对应的权函数的形状。

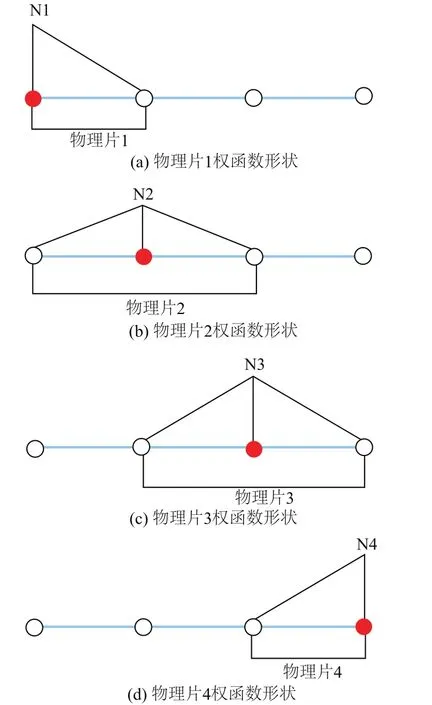
图3 各个物理片对应的权函数形状Fig．3 Shape of weights function on each patch

集中质量矩阵的组装方式有2种：一是按物理片的方式组装；二是按流形单元的方法组装。本文采用按物理片的方法说明组装集中质量矩阵的过程。

惯性力虚功一般形式为

式中：ωi为patch-i所对应的区间；pi为其上的权函数，并满足

其中，

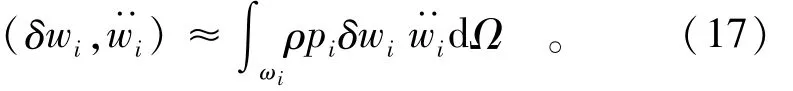
式中：δwi和w··i分别为ωi的虚位移和虚加速度，即ωi上的局部逼近。下面，将从Hermite插值中产生权函数{ pi}和局部近似 {wi}。

设流形单元e由物理片i和j覆盖，其中，来自物理片i的局部近似对挠度w的贡献可表示为

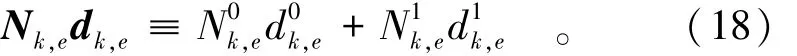
也可以写成

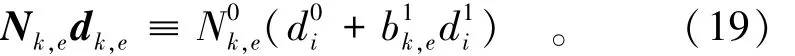
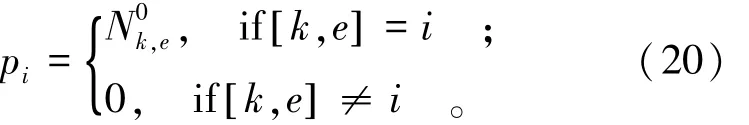
相应的局部逼近为

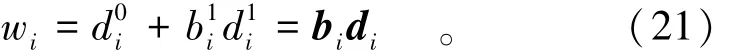
式中 k，e[ ]表示单元e的第k个节点所对应的整体码。相应地有：

将式（23）、式（24）代入式（17），得到

将式（26）代入式（16），得到近似惯性力虚功为

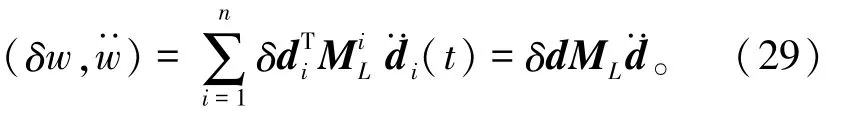
对梁而言，由于有限元网格上的每个结点同时有平动自由度和转动自由度，所以生成的ML为块对角化的质量矩阵，即

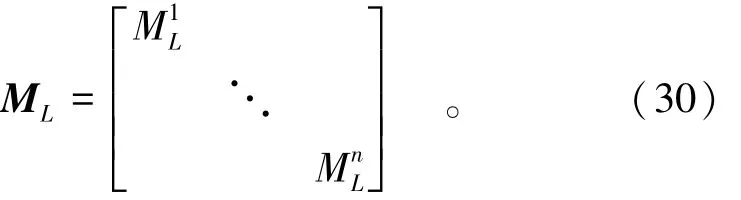
现在，可以直接用块对角化的质量矩阵来求解微分方程组式（13）。然而，为了更好地利用ML这个对称正定的块对角化结构，进行了如下扩展，即将式（30）变换成对角化矩阵。

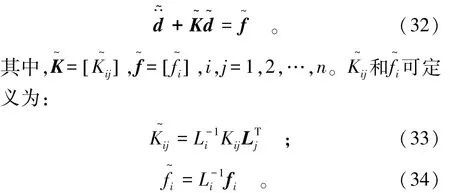
显然，求解新形式的微分方程组（32）相比求解原来的方程组（13）效率要更高。

4 算 例

4.1 欧拉-伯努利（Euler-Bernoulli）梁模态分析

两端简支的Euler-Bernoulli梁，其弹性模量为E＝210 GPa，长度为 1 m，密度为 ρ＝7 860 kg／m3（单位改为正体），截面高和宽都为0.2 m（图4）。将结构划分为40个单元。

图4 等截面梁示意图Fig．4 Rectangular cross-section beam

表1给出了等截面Euler-Bernoulli梁有限元法分别采用一致质量矩阵和集中质量矩阵的前5阶固有频率。在实际测试中发现，随着对单元划分得越细，用本文方法的集中质量矩阵求解速度显著高于用一致质量矩阵。图5为用本方法计算的前5阶模态图。

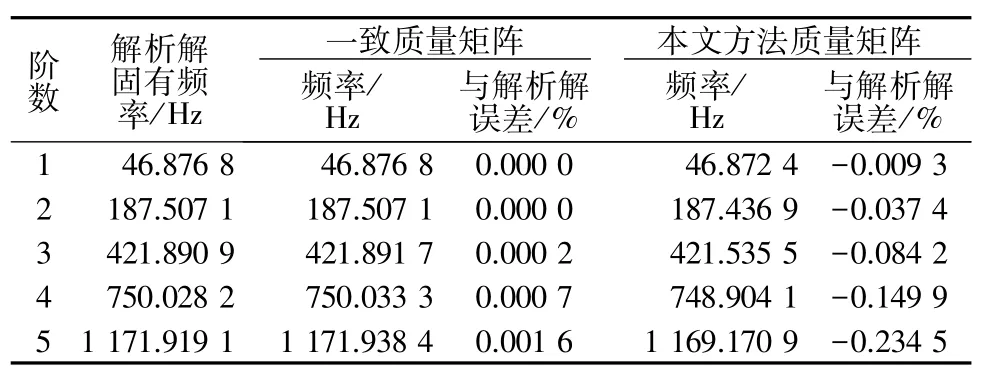
表1 一致质量矩阵与本文集中质量矩阵计算固有频率的对比Table 1 Comparison of natural frequencies for simply supported rectangular cross-section beam between consistent mass matrix and diagonally-lumped mass matrix

从模态分析结果可以看出，使用本文集中质量方法得出的梁结构的前5阶模态和解析解的误差变化在可接受范围内。另外，比较分别采用500个单元和1 000个单元时，用一致质量矩阵和本文方法的速度（计算使用的电脑配置：Intel Core i5-6500＠3.20 GHz，4 GB内存）。结果显示，当将结构划分为500个单元时，后者比前者快约21%；当将结构划分为1 000个单元时，后者比前者快约2倍。显然，计算速度随着结构划分单元数的增加，采用本方法计算高阶模态效应的速度显著高于采用一致质量矩阵方法。

4． 2 Euler-Bernoulli梁的时域分析

两端简支的Euler-Bernoulli梁，参数同本文4.1节，不考虑阻尼的影响。分析在结构中间受到一个简谐荷载F＝F0sin（4πt）作用下的结构中心位置的位移变化情况。

其中，0≤t≤td，计算总持续时间td为1 s，时间步取0.001 s。这里，分别使用时域逐步积分法中的中心差分法和Newmark-β法来求结构中点的位移变化。

图6（a）是采用一致质量矩阵的结果，图6（b）是采用本文提出的对角化集中质量矩阵的结果。由图6、表2可以看出，使用本文集中质量矩阵方法得出的梁结构的时域反应和采用一致质量矩阵的时域反应相差很小。

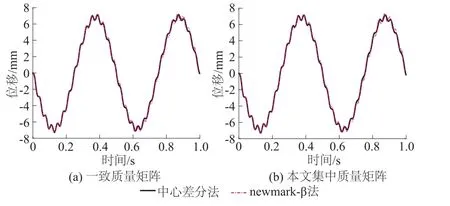
图6 时域计算的结构中点的位移变化情况Fig．6 Variations of displacement of center block of beam with step-by-step methods using consistent mass matrix and diagonally-lumped mass matrix

表2 一致质量矩阵与本文集中质量矩阵计算简谐荷载作用下梁中心点位移的对比Table 2 Comparison of center displacement under harmonic load for simply supported rectangular cross-section beam between consistent mass matrix and diagonally-lumped mass matrix

5 结 语

从算例可以看出，在流形上积分，构造的数学严格的集中质量矩阵的方法不仅能够有效地提高运行效率，对二维问题中的8节点等参元，用本方法克服了一般的集中质量矩阵不满足角点正定性要求。更可贵的是，本方法有着严格的数学基础和力学基础。可以预见的是，本方法对于二维乃至三维结构（以板壳结构为典型代表）的动力计算有着天然的优越性。

因此，无论是直接积分法中显式方法，还是隐式方法，无论是时域分析，还是频域分析，都可用本文所建议的集中质量矩阵代替一致质量矩阵。