重力坝多滑面深层抗滑稳定计算的优化方法
2019-04-24彭文明
彭文明
(中国电建集团成都勘测设计研究院有限公司勘测设计分公司,成都 610072)
1 研究背景
混凝土重力坝依靠自重抵抗上游水推力,其坝基抗滑稳定是重点关心的技术问题,尤其是深层抗滑稳定,往往成为大坝安全的控制因素。经过一个世纪的演变发展,形成了以刚体极限平衡方法为基础的重力坝深层抗滑分析多种计算方法[1]。深层稳定计算的滑移模式一般以单滑面和双滑面为主,多滑动面在工程实践[2-5]中也经常遇到。
为解决工程实际问题,美国陆军工程师团和我国国家能源局发布的重力坝设计规范中都给出了多滑面抗滑稳定计算公式[6-7]。多滑动面抗滑稳定计算以刚体极限平衡方法为基础,不考虑滑块力矩平衡,对每个滑块进行条分,并定义各滑块抗滑稳定安全系数,或采用分项系数设计方法的各滑块抗力作用比。按照潘家铮的“最大最小原理”[1],各滑块可通过调整滑块之间的作用力ΔQi,以发挥最大的抗滑能力。此时,滑动体系达到极限平衡,各条块具有同等的抗滑稳定安全度,即坝基整体抗滑稳定安全系数FS或抗力作用比η。
根据上述计算原理,滑块之间的未知作用力ΔQi对于坝基抗滑作用体系至关重要。随着滑块数量增多,稳定计算的未知变量增多,其求解难度也进一步提升。为此,我国规范[7]在给出计算公式的同时,给出了方程求解思路。由于计算公式较为复杂,而求解思路过于简单,在工程实践中的指导作用不大,计算理论体系的不严谨甚至可能会误导工程师。美国规范[6]虽然给出了详细的求解方法,但由于其计算公式中假定滑块抗力合力为水平方向,与我国规范有一定差异,不能简单套用。
鉴于规范方法存在的不足,本文在刚体极限平衡理论框架基础上,寻求坝基多滑面深层抗滑稳定计算的优化方法。
2 规范方法及其不足
2.1 规范中的多滑面计算方法
本文主要针对中国规范方法[7]展开分析,并对美国规范的计算方法[6]进行简要阐述。
2.1.1 中国规范方法
我国国家能源局发布的《混凝土重力坝设计规范》[7],给出了采用分项系数法的重力坝多滑面深层抗滑稳定计算公式(以下简称中国规范方法)。图1(a)为坝基抗滑稳定计算剖面,单个条块受力如图 1(b)所示。
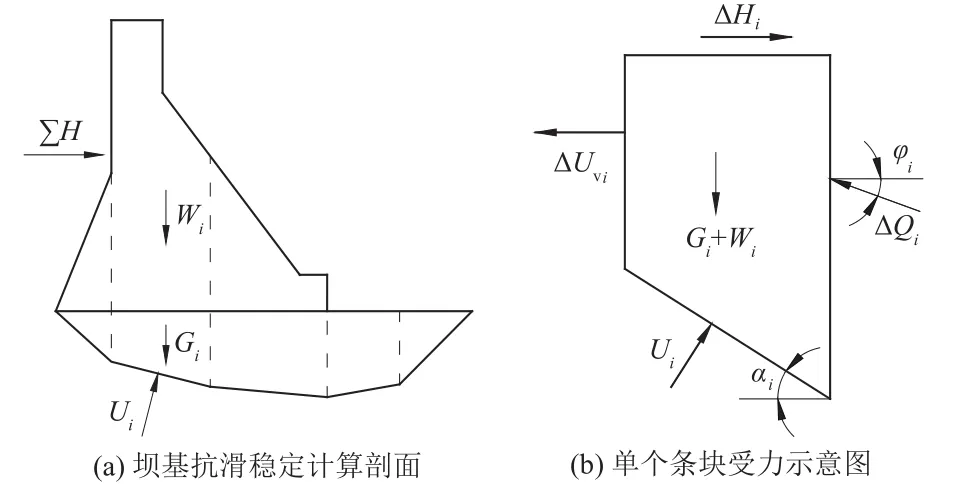
图1 中国规范方法坝基抗滑稳定计算示意图Fig.1 Sketch of slide-resistant stability solution for dam foundation in Chinese standard
图1 中:ΣH为坝面水平推力;Wi为滑块上覆坝体重力;Gi为滑块重力;Ui为滑块底滑面所受水压力;αi为底滑面倾角,以倾向下游为正;ΔHi为滑块所受其他水平向荷载;ΔUvi为滑块两侧面水压合力;ΔQi为该滑块两侧剪力合力,以指向上游为正;φi为ΔQi与水平向夹角,假定为已知。
单个滑块的抗力函数R(·)和作用函数S(·)可分别表示为:
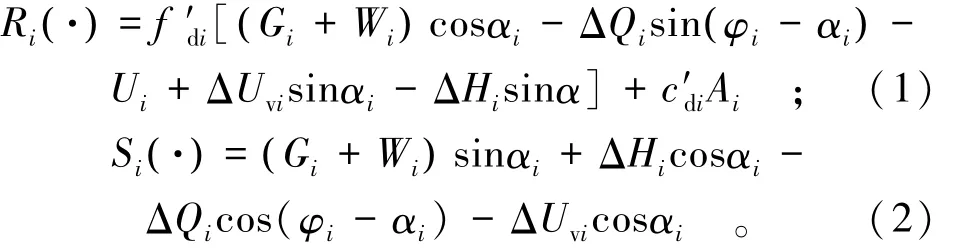
式中:f′di为底滑面的抗剪断摩擦系数;c′di为底滑面的抗剪断凝聚力;Ai为底滑面面积。
式(1)和式(2)中的荷载和材料性能均采用设计值计算。
定义各条块抗力作用比ηi如式(3)所示,滑动体系各条块具有同等的抗力作用比η,此时滑动体系达到极限平衡,即坝基整体抗力作用比η。
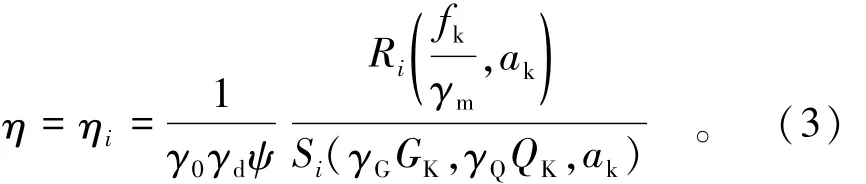
式中:γ0为结构重要性系数;γd为承载能力极限状态的结构系数;ψ为设计状况系数;fk为材料性能的标准值;γm为材料性能的分项系数;ak为几何参数的标准值;γG为永久作用的分项系数;GK为永久作用的标准值;γQ为可变作用的分项系数;QK为可变作用的标准值。
对于同一坝基断面而言,γ0,γd,ψ三者的数值相同,式(3)可简化:
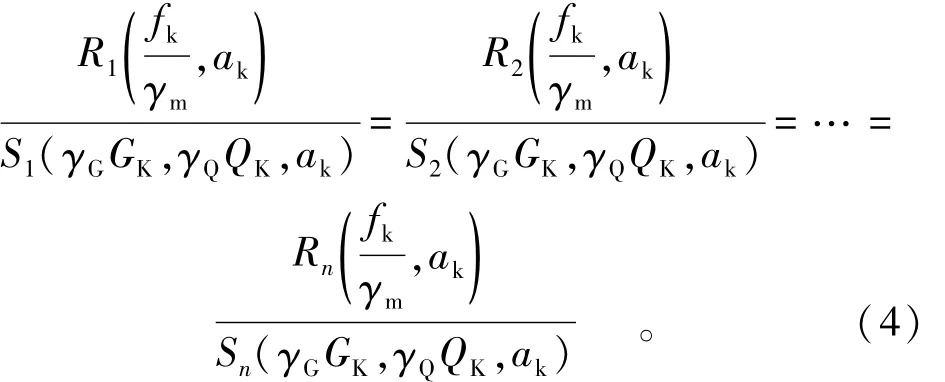
由式(4)可得到n-1个方程,其中含有n个未知数ΔQi,再由坝基体系内力平衡条件可得
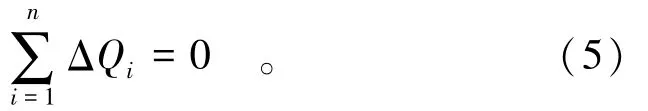
规范[7]提出,由式(4)和式(5)联立求解得到各滑块侧向接触面间的剪力ΔQi,再返回代入式(3)可得到抗力作用比η,从而完成抗滑稳定计算。当η≥1时,即认为满足稳定要求。
2.1.2 美国规范方法
美国陆军工程师团的重力坝设计规范[6]采用单一安全系数法进行重力坝多滑面深层抗滑稳定计算(以下简称美国规范方法),其安全系数Fs计算表达式为:
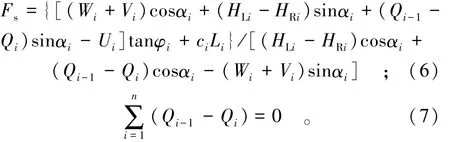
式中:Vi为外部竖向力;HLi和HRi为左侧和右侧接触面顶部以上及底部以下的外部水平力;Wi为滑块自重;Ui为滑面扬压力;Qi为滑块之间抗力(规定为水平向);φi和 ci分别为滑面的抗剪断摩擦角和凝聚力;Li和 αi分别为滑面长和倾斜角度。条块受力示意图见图2所示。
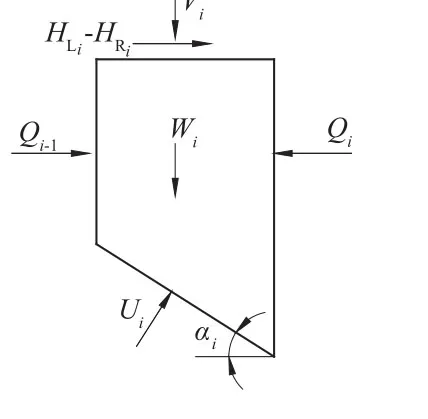
图2 美国规范方法计算单个条块受力示意图Fig.2 Force diagram of single sliding block in US standard
美国规范给出了具体求解过程,主要步骤为:
(1)假定 Fs初始值。
(2)由式(6)计算各滑块抗力合力 Qi-1-Qi。
(3)由式(7)判定Fs是否为方程的解。
(4)若不满足式(7),则调整 Fs,返回步骤(2)重新迭代计算。
(5)若满足或近似满足式(7),则计算终止。
2.2 规范方法的不足之处
中美规范均采用条块两侧抗力的合力(以ΔQi表示)为未知量进行计算求解,其中中国规范假定ΔQi与水平向有一夹角φi,美国规范假定ΔQi为水平向,即 φi=0。
进一步分析可知,上述处理存在2个不足:未知变量ΔQi的物理意义不清晰和对变量ΔQi进行标量求和值得商榷。
2.2.1 未知变量ΔQi的物理意义不清晰
合力ΔQi及其作用方向φi,隐含了滑块两个侧面上的抗力Qi-1和Qi的大小及方向信息。由于计算公式为标量表达式,未知变量ΔQi无法完整表达两个侧面上抗力的物理意义。比如计算出Qi为负值时,可以通过分析该接触面是否允许出现拉应力来判断求解结果是否具有物理意义;但是当ΔQi为负值时,工程师无法确定其是否具有物理意义,即解的合理性无法判定。
美国规范假定ΔQi为水平向,求解确定的是刚体极限平衡条件下水平作用力平衡的整体安全系数Fs。事实上,滑块之间的接触面方向是不固定的,滑块往往沿薄弱层面剪切破坏。当坝基节理裂隙发育时,沿裂隙的方向错动破坏更符合实际情况。与此同时,影响抗力Qi作用方向的因素也较多。根据工程经验,取接触面竖直且Qi为水平方向,通常更不利于坝基抗滑,安全系数相对较小[8-9]。美国规范采用的简化处理偏于保守,计算公式缺乏灵活性,在特定条件下难以真实模拟实际情况。
2.2.2 对变量ΔQi进行标量求和值得商榷
中国规范方法以ΔQi为变量,其作用方向为φi(与水平向夹角,指向上游为正)。很显然,各滑块的ΔQi作用方向不相同。由于每个滑块之间的抗力为内力,应满足ΔQi水平向和竖向的分量求和均等于0。美国规范假定Qi为水平向,采用式(7)进行标量求和是可行的;而我国规范采用式(5)对ΔQi进行标量求和缺乏物理意义。当φi各不相同时,所有内力ΔQi平衡应采用矢量表达式,即
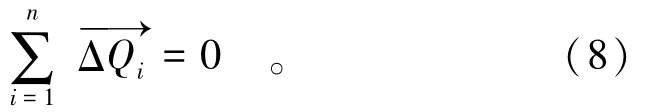
对于二维计算,式(8)为水平向和竖向2个平衡方程。若以式(8)替换式(5),与式(3)联立,则方程数为n+2,多于未知数,也无法完成计算,问题在于计算中假定ΔQi的作用方向φi均为已知。事实上,n个滑块相互作用时,已知n-1个滑块的ΔQi及作用方向φi时,可以求出第n个滑块的ΔQi及φi。所以,规范方法假定n个φi均为已知,存在冗余假设。
因此,中国规范方法以作用方向不为水平的ΔQi作为未知变量求解多滑面抗滑稳定安全系数(抗力作用比),其理论体系不严谨。在φi不相等时,求解得出的结果可能是错误的。
3 多滑面抗滑稳定计算的优化方法
由于多滑面计算中,式(3)—式(5)以滑块两侧抗力之和ΔQi为未知变量,同时假定ΔQi的方向φi均为已知数,存在诸多问题,可能导致错误的计算结果。为此,本文提出优化解法。
3.1 计算方法优化
本文提出用滑块之间接触面上的抗力Qi代替ΔQi,还原滑块受力的物理本质意义,其他计算条件不变,按照如下步骤修正规范公式。
(1)定义条块i与条块i+1之间的抗力Qi及其与水平向夹角 φ′i,则有:
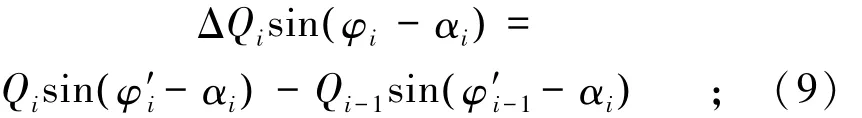
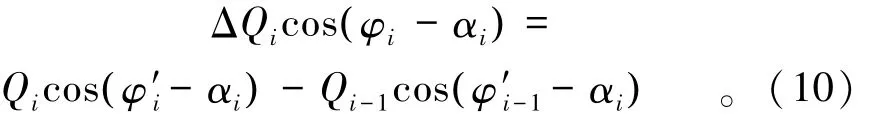
式中:Qi为滑块i与滑块i+1之间的抗力,以压力为正,拉力为负;φ′i为Qi与水平向夹角。
特别地,当i=1以及i=n时,滑块单侧面受抗力,有 Q0=Qn= 0,式(9)和式(10)简化为 i=1时,有
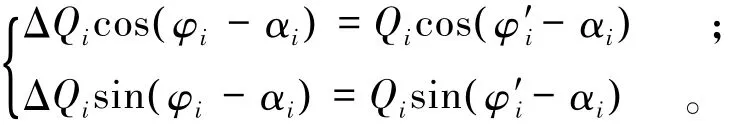
i=n时,有
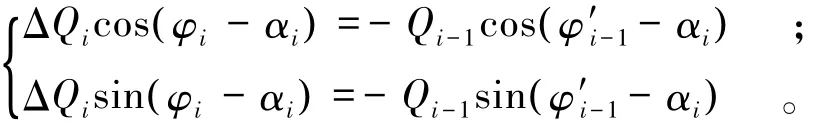
(2)将式(9)代入式(1),式(10)代入式(2)得:
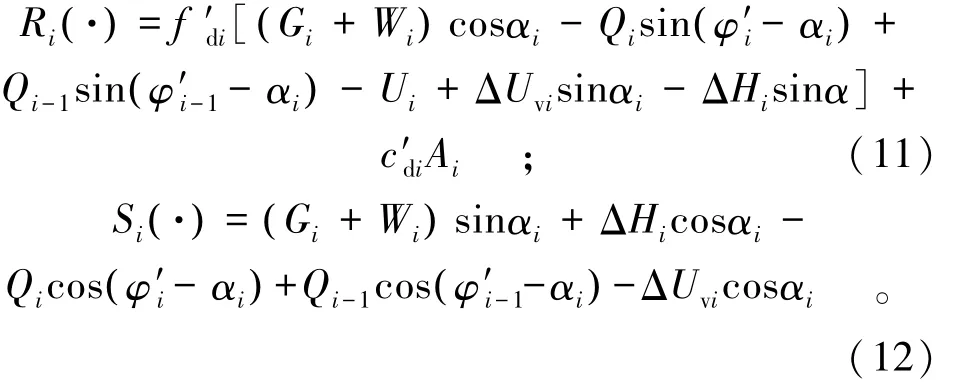
变换后,将式(11)、式(12)代入式(3),得
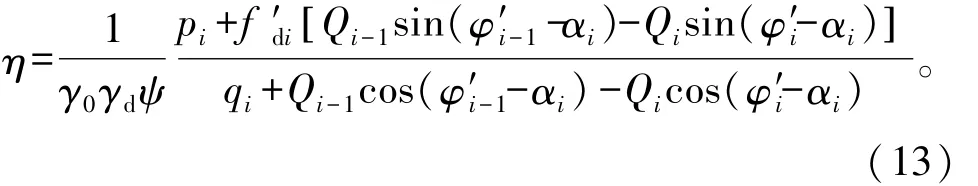
其中 pi和 qi为已知量,其表达式分别为:pi=
由前述假定,当 i=1时,Qi-1=0;i=n时,Qi=0。因此式(13)为 n个方程,其中含有 n个未知数:Qi(i=1,2,…,n-1)和 η。
进行上述公式修正后,方程未知变量Qi物理意义更清晰,计算变量φ′i也具有直接的力学意义。参考文献[1],抗力与水平面夹角tanφ′i取值范围宜为[0,f′/Fs],这里 f′指接触面上的摩擦系数。
3.2 优化方法的求解
3.2.1 迭代求解方法
式(13)的每个方程式拥有共同的未知变量η,可以采用单变量迭代求解(见图3)优化求解方式。
计算的具体步骤如下:
(1)假定初始抗力作用比η(为简化表述,η已包含 γ0γdψ),并代入式(13)。
(2)由滑块 1可求 Q1,即
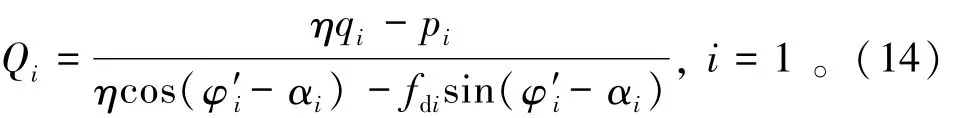
(3)已知Q1后,由滑块2可求Q2;依次递推由滑块 i(i=3,…,n-1)可求解 Qi(i=3,…,n-1),即
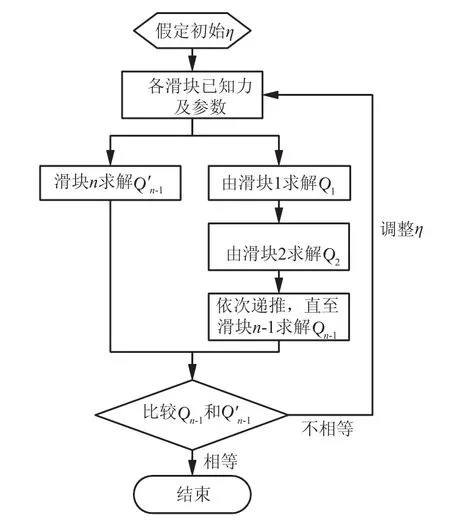
图3 优化方法的迭代求解思路Fig.3 Iterative solution of the optimized method
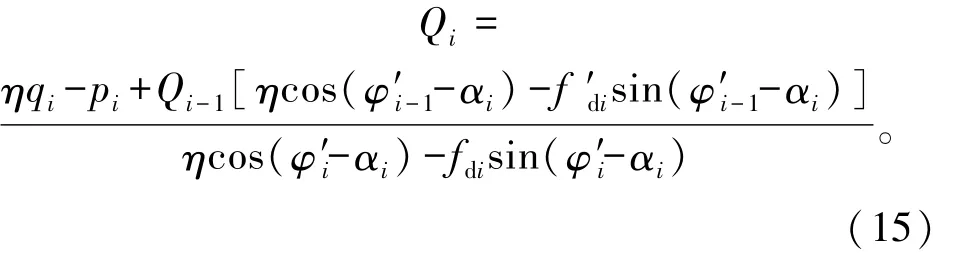
(3)同时,当抗力作用比为η时,由滑块n也可求出滑块n与滑块n-1之间的推力,记为Q′n-1,即
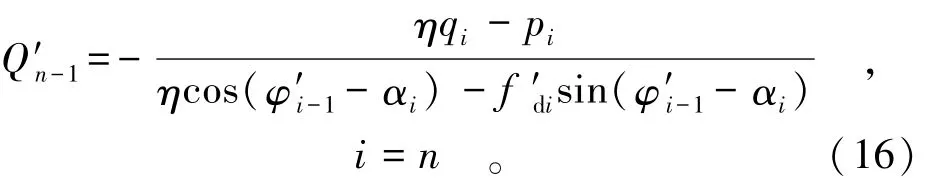
完成步骤(1)—步骤(3)后,可得到第1次迭代的结果Qi(i=1,2,…,n-1)和Q′i。如果η为方程真解,则有Qn-1=Q′n-1;否则,Qn-1≠Q′n-1。因此,计算中可对η进行调整试算,反复求解Qn-1和Q′n-1,直到获得近似解为事先给定的任意小的数,是收敛控制标准),从而结束迭代过程。
3.2.2 迭代收敛分析
本文方法的迭代求解是以假定η来求解滑块之间的剪力Qn-1,所以式(13)可以看作是η与Qn-1之间的函数,即
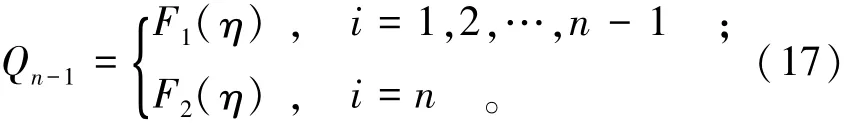
根据Qi和η的物理力学意义,可以分析式(17)是单调函数。
(1)把滑块1—滑块n-1作为整体考虑,该滑移体系的未知外力为Qn-1,而且Qn-1是抗力,显然随着η的增大,需要的抗力 Qn-1也越大,因此函数F1(η)单调递增。
(2)对滑块n而言,Qn-1是作用力,对滑块n的抗滑是不利的,显然随着η的增大,作用力Qn-1应减小,因此函数 F2(η)单调递减。关于 F1(η)和F2(η)的单调性判断,在拱坝坝肩稳定分析[10]中可得到类似的结论。
根据 F1(η)和 F2(η)的单调性,可以绘制函数曲线示意图(如图 4所示)。对于给定的 ηk,可以通过比较 Qn-1=F1(ηk)和 Q′n-1=F2(ηk)的大小,判断 ηk与曲线交点 η′0(即方程的解)的位置关系,从而获得下一次迭代ηk+1的调整路径,使得ηk+1与η′0越来越接近。因此,对于一般情况,本文迭代求解方法是可以收敛的。
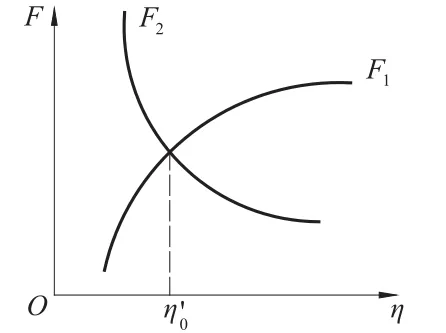
图4 F 1(η)和 F 2(η)函数曲线Fig.4 Function curves of F 1(η)and F 2(η)
4 工程应用
4.1 典型算例
本节通过典型算例分析不同计算方法的差异。图5所示的典型算例,坝基宽70 m,扬压力折减位置距坝踵10 m,折减系数取0.25。大坝和基岩重度分别为 24 kN/m3和 26 kN/m3,淤沙浮重度取 6 kN/m3、内摩擦角12°。
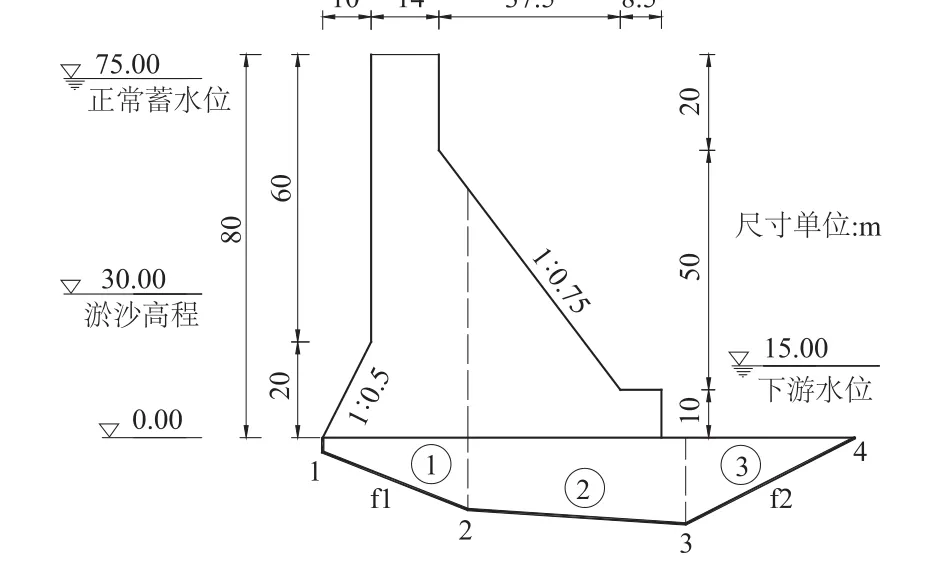
图5 典型算例计算剖面Fig.5 Profile of typical example
典型算例中滑移通道相关参数如表1所示。

表1 典型算例滑移通道计算参数Table 1 Calculation parameters of slip surfaces in the typical example
本例主要为验证计算方法的可行性,为方便不同方法对比,材料性能和作用分项系数以及γ0,γd,ψ均取1,计算结果η即为单一安全系数法的Fs。本例的荷载计算成果如表2所示。
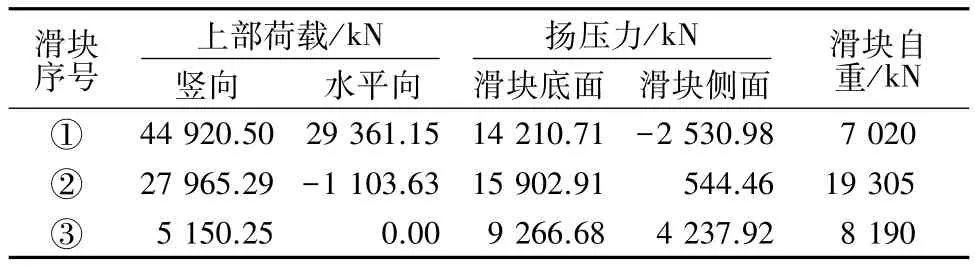
表2 典型算例荷载成果Table 2 Calculated result of load in the typical example
在确定滑块之间抗力的角度时,如前所述,抗力与水平面夹角的正切值 tanφ′i取值范围宜为[0,f′/Fs],下面分别取 tanφ′i为 0(方案 1)和 f′/Fs(方案2)2种方案进行计算。本例的坝基裂隙较为发育,以裂隙的摩擦系数0.8作为滑块①和滑块②之间接触面的f′,以新鲜岩石的摩擦系数1.0作为滑块②和滑块③之间接触面的f′。
下面分别采用本文优化方法、中国规范方法、美国规范方法进行对比计算。
首先采用本文优化方法计算,可以得到2种方案的安全系数分别为2.97和3.56(见表3),方案2安全系数提高幅度达到19.9%,此时2个接触面的抗力角度分别为12.65°和15.67°。
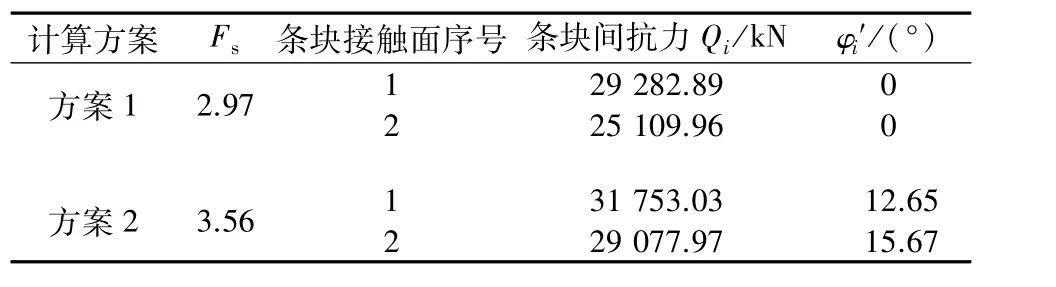
表3 典型算例按本文优化方法的计算结果Table 3 Calculation result by the proposed optimized method for the typical example
然后采用中国规范方法,计算需要输入条块抗力合力的角度。对于方案2,考虑到滑块①和滑块③只受单面推力,抗力合力的方向φi与φ′i数值相同;而滑块②抗力合力的方向取决于两侧接触面抗力的大小及方向,因此难以确定。本文计算中,做如下2种处理方式:
(1)取滑块②滑移通道的摩擦系数0.5作为输入参数,通过 f′/Fs计算合力方向,即 tanφ2=0.5/Fs,此方式记为方案2(1)。
(2)φ2取 φ1和 φ3的平均值,此方式记为方案2(2)。
值得说明的是,方式(1)和方式(2)均没有实际物理意义,此处仅为计算的简化处理。
采用中国规范公式,参考美国规范求解思路,联立式(3)和式(5)求解,计算结果见表4。
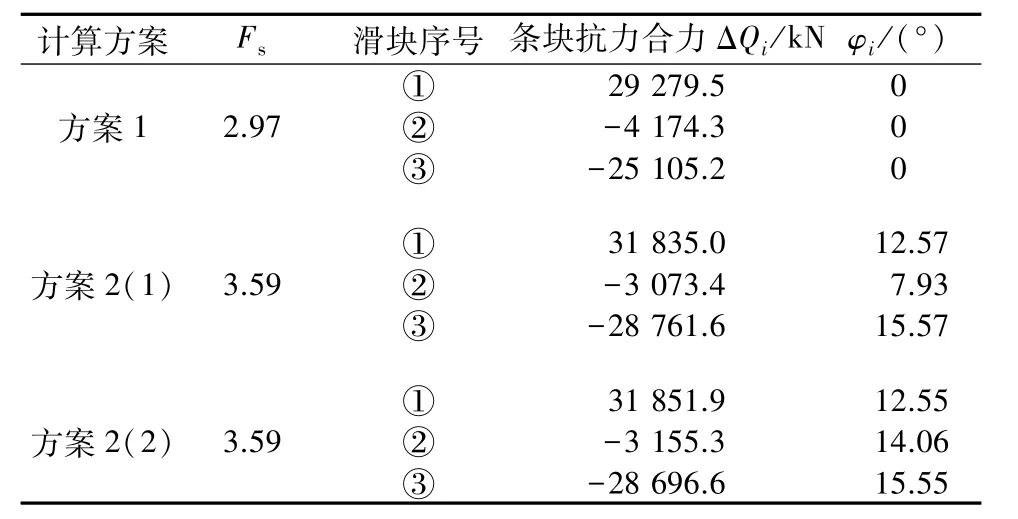
表4 典型算例按中国规范方法的计算结果Table 4 Calculation result by the method in Chinese standard for the typical example
对比表3和表4可以看出,两种方法方案1的安全系数的计算结果完全相同,方案2安全系数有一定差异,采用中国规范公式的安全系数为3.59,比本文方法略大。对比方案2(1)和方案2(2),由于本例滑块②的抗力合力绝对值不大,虽然方案2(1)和方案 2(2)的 φ2相差较大(前者7.93°,后者14.06°),但是安全系数总体相同。
规范公式以式(5)作为求解方程,只满足内力大小∑ΔQi等于 0,由于 ΔQi的方向 φi不同,对方案2(1)和方案 2(2)各条块抗力合力(kN)进行向量求和,可得
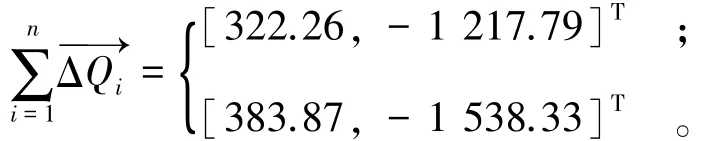
显然,条块抗力合力实际上不平衡,不满足刚体极限平衡条件,计算结果存在一定误差。
之后采用美国规范方法,因其假定条块抗力合力为水平,因此只计算方案1,计算结见表5。

表5 典型算例按美国规范方法的计算结果Table 5 Calculation result by the method in US standard for the typical example
从表5中的计算结果可知,美国规范方法计算的安全系数比本文优化方法和中国规范方法要高,主要原因是美国规范不考虑条块侧面水压力的作用。一般情况下,滑块之间的侧面水压力属于内力,计入与否对计算结果没有多大影响,但滑块①的上游侧面和滑块n的下游侧面例外。由于岩体有裂隙的存在,在滑移体系刚体极限平衡条件下,对滑块①的上游侧面和滑块n的下游侧面计入水推力可能更为合理。本例滑块①的上游侧面高3 m,美国规范不考虑该侧面的水推力,因此安全系数偏大。
4.2 官地溢流坝抗滑稳定计算
图6为官地水电站典型溢流坝段剖面示意图,建基面高程1 166 m,溢流坝基面长度153.2 m,下游护坦顶面高程1 188 m;上下游水位分别为1 330 m和1 203.7 m,混凝土和基岩密度分别取2.52 g/cm3和2.70 g/cm3,坝体按Ⅷ度地震烈度设防,相应地震加速度为0.284 g。坝基错动带分布复杂,其中fxh01,fxh05,fxh07容易贯通形成深层滑动通道。
根据错动带分布特点,拟定计算通道为1-2-3-4-5-6,其中错动带之间用岩桥连接。滑移通道控制点坐标及底滑面力学参数如表6所示。

图6 官地水电站溢流坝剖面示意图Fig.6 Profile of the spillway dam of Guandi hydropower station

表6 官地溢流坝段滑移通道计算参数Table 6 Calculation parameters of slip surfaces for Guandi spillway dam
抗滑稳定计算中,分别考虑tanφ′i为0(方案1)和f′/Fs(方案2)2种方案,其中接触面上的摩擦系数综合考虑坝基岩石结构面发育程度、岩石埋深等因素进行取值,见表7。

表7 滑块接触面摩擦系数Table 7 Friction coefficients of contact wedges
4.2.1 单一安全系数Fs
用不同方法计算滑移通道1-2-3-4-5-6的抗滑稳定安全系数Fs。
采用本文优化方法的计算结果见表8。从表中的计算结果可以看出,正常蓄水和地震工况的安全系数,方案1分别为2.91和2.11,方案2分别为3.21和2.40,提高幅度为10.3%和13.7%,取一定抗力角度对安全系数提高是很明显的。
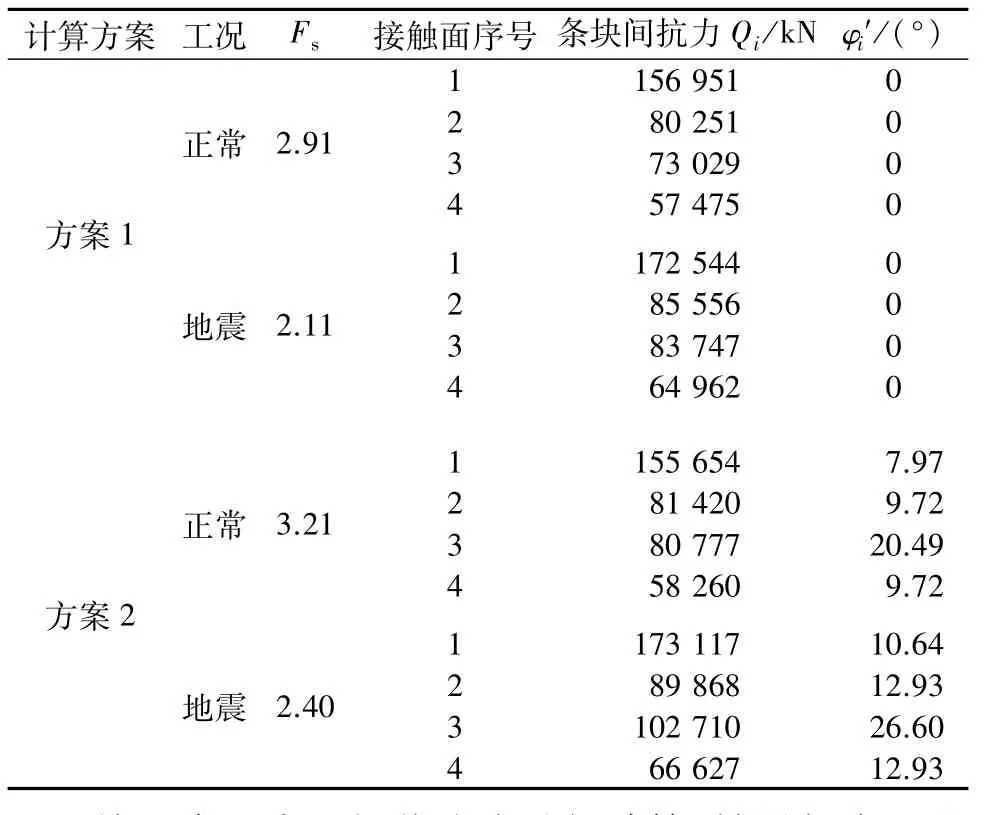
表8 官地溢流坝按本文优化方法的抗滑稳定计算结果Table 8 Calculation result of anti-sliding stability of Guandi spillway dam by the proposed optimized method
接下来用中国规范公式进行计算,结果如表9所示。值得说明的是,方案2中对各滑块抗力合力角度取值时,滑块②—滑块④的抗力合力角度由于受各滑块两侧面未知抗力的影响,是个不确定量。计算中取相应滑块滑移面的f′di作为输入,即tanφi=f′di/Fs,这种做法并无理论依据,只是一种简化处理方式。
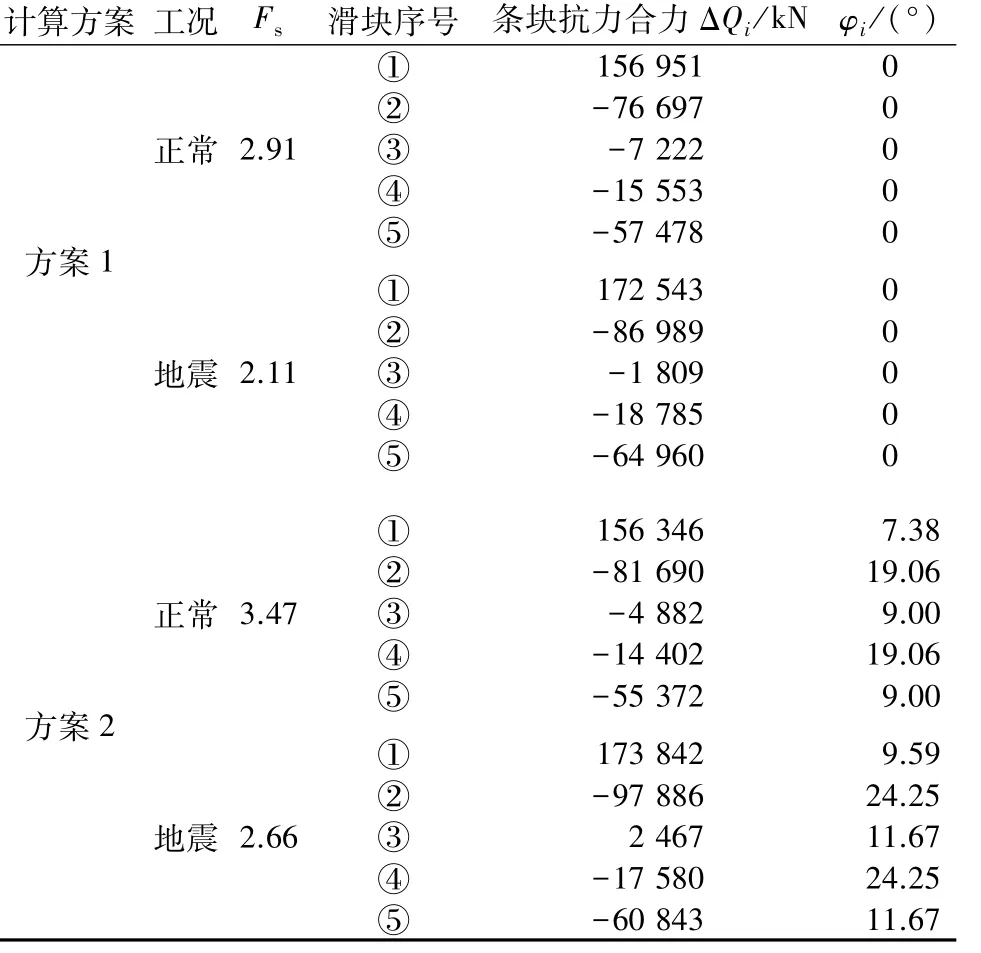
表9 官地溢流坝按中国规范方法的抗滑稳定计算结果Table 9 Calculation result of anti-sliding stability of Guandi spillway dam by the method in Chinese standard
对比表8和表9,2种方法的方案1无本质差异,各工况安全系数相同;对于方案2,规范公式安全系数明显大得多,分别为3.47(正常工况)、2.66(地震工况),比本文方法提高8.1%(正常工况)和10.8%(地震工况)。
规范方法安全系数提高的原因,是由于抗力合力只满足式(5)而未满足力的矢量平衡。事实上,对表9方案2的条块抗力合力(kN)进行向量求和,可得:
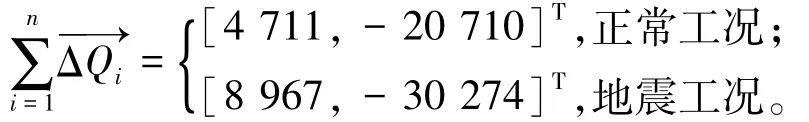
由于ΔQi以指向上游为正,其水平分量以向上游为正、竖向分量以竖直向上为正。从上述计算可知,抗力合力存在很大的不平衡量,其中竖向不平衡力分别为-20 710 kN(正常工况,向下)和-30 274 kN(地震工况,向下),相当于额外增加滑块竖向荷载,其量值达到坝体总重(306 276 kN)的6.8%和9.9%,显然这不科学。
4.2.2 分项系数法的抗力作用比η
鉴于中国规范采用分项系数设计方法,本文也进行考虑分项系数的抗力作用比计算,进一步考察2种方法的计算规律。计算方案与前面相同,结果见表10。
从表10可知,2种方法中方案1的计算结果相同;方案2的变化规律与安全系数Fs类似,2种方法考虑抗力角度后抗力作用比η均有提高,其中正常工况和地震工况下本文优化方法的方案2比方案1分别提高15.0%和13.1%;而中国规范方法提高幅度更大,正常工况和地震工况下在本文方法方案2的基础上进一步分别提高13.0%和11.6%。
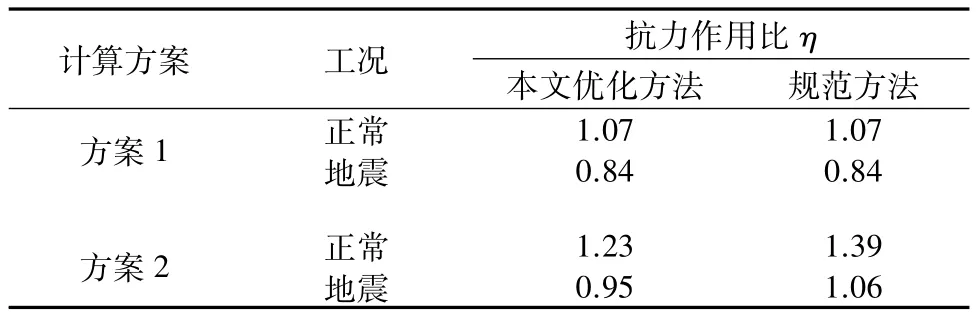
表10 官地溢流坝抗滑稳定计算的抗力作用比Table 10 Resistance-action ratio of anti-sliding stability calculated for Guandi spillway dam
综合上述分析,中国规范方法虽然指出条块抗力合力与水平面的夹角为已知,由于该角度取值缺乏理论依据,很难进行实际操作;加上式(5)不满足抗力合力的矢量平衡,最后导致错误的计算结果。本文优化方法用条块侧面上的抗力作为变量,很好地解决了规范方法的不足,计算中体现出较好的优越性。
5 结 语
我国重力坝设计规范给出了多滑动面深层抗滑稳定计算方法。规范假定条块抗力ΔQi与水平向夹角φi不为0,利于更为真实地模拟实际情况,同时也提高了方程求解计算难度。规范方法以ΔQi满足内力平衡条件求解抗力作用比η。在φi不相同的情况下,用式(5)进行ΔQi的标量求和没有物理意义,未能真正满足内力矢量平衡。因此,规范方法的理论体系不严谨,在φi不相等时求解结果可能是错误的。
鉴于规范方法的不足,本文以条块之间的剪力Qi替换ΔQi,对规范公式进行修正,并提出基于单变量η的迭代求解方法。优化解法解决了规范存在的问题,计算公式物理意义更清晰,迭代求解可操作性强,提高了多滑面稳定计算的实用价值。通过典型算例和工程实例,进一步验证了规范方法的不严谨可能导致不可接受的错误结果,同时证明了本文优化方法的准确性和实用性。
值得注意的是,计算表明考虑抗力角度对于提高抗滑稳定安全系数效果很明显,但由于条块之间抗力相互传递作用的机理较为复杂,工程实践中对φ′i的确定应慎重。
