聚焦思想方法 提升解题能力——核心素养背景下的高考复习策略初探

贵州 胡道成

高考题非常注重学科方法和思维方法的运用能力，高考答题是一个知识的选择、组合、运用的智力活动。高考备考教学过程中必须把“思想方法”突显出来，把概念、定理、定律、公式等知识联系起来形成结构。教学过程中要提高学生的解题能力，就必须聚焦思想方法，把物理思想方法和特殊思维方法的应用能力作为一项重要策略来提升，有针对性的引导学生去思考、领悟、感知、品味、体验，逐步提高学生面对新颖的、陌生的实际问题时能自觉、独立地运用科学思想方法分析、论证并运用相关物理知识解答问题的能力。

一、建构物理模型，寻找基本知识、规律的运用途径

【例1】(2018年全国Ⅱ卷第16题)2018年2月，我国500 m口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”，其自转周期T=5.19 ms，假设星体为质量均匀分布的球体，已知万有引力常量为6.67×10-11N·m2/kg2。以周期T稳定自转的星体的密度最小值约为

( )

A.5×109kg/m3B.5×1012kg/m3

C.5×1015kg/m3D.5×1018kg/m3

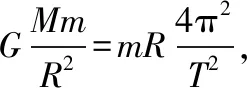
【备考启示】建立合适的物理模型是思维的关键，高中物理涉及二十多种物理模型，教学过程中要善于引导学生识别实物现象中的物理模型，准确联想到相关的物理概念、规律和公式，进而寻找已知量与待求量之间的具体关系。

二、结合生产、生活经验，围绕物理知识、规律提高估算能力

【例2】(2018年全国Ⅱ卷第15题)高空坠物极易对行人造成伤害。若一个50 g的鸡蛋从一居民楼的25层坠下，与地面的碰撞时间约为2 ms，则该鸡蛋对地面产生的冲击力约为

( )

A.10 N B.102N

C.103N D.104N

【备考启示】解答估算题通常需要建立物理模型，同时使用生产、生活中积累的常识性数据、采用合理取舍的数学近似方法处理，进行科学的推理和论证。高中物理的教学过程不应该是一个“两耳不闻窗外事，一心只读圣贤书”的“书山题海”死记硬背过程！

三、培养科学想象能力，在严密的逻辑联系中去推理、综合与分析

【例3】(2018年全国Ⅰ卷第18题)如图1，abc是竖直面内的光滑固定轨道，ab水平，长度为2R；bc是半径为R的四分之一圆弧，与ab相切于b点。一质量为m的小球，始终受到与重力大小相等的水平外力的作用，自a点处从静止开始向右运动。重力加速度大小为g。小球从a点开始运动到其轨迹最高点，机械能的增量为

( )

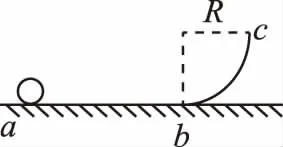
图1

A.2mgRB.4mgR

C.5mgRD.6mgR

【备考启示】爱因斯坦说过：“想象力比知识更重要，因为知识是有限的，而想象力可概括世界上的一切，推动着进步，并且是知识进化的源泉。”在2018年高考题命题中采用引入这种隐形“场”(题图不给出)考查学生“想象能力”的题目还有全国Ⅱ卷第20题“整个系统处于匀强外磁场中”和全国Ⅲ卷第25题“小球还一直受到一水平恒力”。解题时加上这个隐形场的场线引导以维持严密的思维逻辑是至关重要的。本题还设下了一个让考生错误率很高的“陷阱”，即易把“轨迹最高点”当成“轨道最高点”，观察能力也很重要。

四、把握基本规律，以不变应万变，定性与半定量相结合

【例4】(2015年全国Ⅰ卷第20题)如图2(a)，一物块在t=0时刻滑上一固定斜面，其运动的v-t图线如图2(b)所示。若重力加速度及图中的v0、v1、t1均为已知量，则可求出

( )

图2

A.斜面的倾角

B.物块的质量

C.物块与斜面间的动摩擦因数

D.物块沿斜面向上滑行的最大高度

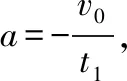
【备考启示】本题通过图象来考查学生的物理方法，只要抓住“一看轴，二看线，三看斜率，四看面积，五看截距，六看点”这些常规的思路识别出斜率、面积、截距的物理意义并结合物体的运动情况，选择牛顿第二定律和恰当的运动学公式就很容易通过分析、推理得出结果。根本没必要算出具体结果，只需要适当的计算就可推理出θ、μ和最大高度能够求出来即可。只会低头计算不会抬头思考是徒劳而费时的，要把定性分析与半定量方法有机结合起来，实现提速增效。合理使用量纲分析法、对称分析法、数量级估算法、特殊值分析法等能够做出判定的，能不算就不算。

五、抓住思维起点，注重优选公式和算法，宁可直中取，不在曲中求

【例5】高尔夫是一种把享受大自然的乐趣、体育锻炼和游戏集于一身的运动，看重绅士风度之展现。比赛要求球处于静止状态才可开始。在某次比赛中，一名高尔夫运动员击球后球恰好落在洞的边缘，洞纵切面恰好是半径为R的半圆，如图3所示，假设忽略空气阻力，重力加速度为g，把此球以大小不同的初速度v0沿半径方向水平击出，球落到圆周上，则下列说法正确的是

( )

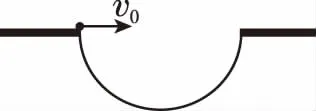
图3

A.v0越大，运动时间越长

C.调整v0大小到合适，球就会垂直击在圆周上

D.无论v0多大，球都不会垂直击在圆周上

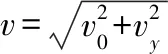
【备考启示】识别模型，将题给情境进行同化，在脑海中迅速搜索出相关“子结论”，充分利用推论实现“以题攻题”是一种高阶思维能力，养成这种思维习惯往往具有事半功倍的效果。再比如2018年全国Ⅱ卷第21题的解答过程中就需要用到“匀强电场中同一条直线上两点间的电势差与两点间的距离成正比”这一推论。思维品质的优化是解题过程中必须考虑的问题，平时要善于引导学生看准题干，弄清情境，切勿在解题过程中急于求成而忘记了为什么出发，落入自寻烦恼的困境中。

六、充分利用逆向思维法、极限法、对称法、微元法、等效法等特殊思维方法参与解题，可以提升思维品质，出奇制胜

【例6】(原创题)如图4所示，热气球及吊篮的质量为M，有一质量为m的玩具篮球放置于吊篮中，起初它们一起以加速度a上升，当玩具篮球(体积可以忽略)突然从吊篮中掉落时，热气球及吊篮上升的加速度将变为

( )

图4

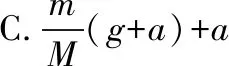
【思路分析】本题可以根据牛顿运动定律列方程求解。但如果我们考虑特殊情况，即：将掉落的篮球质量m认为等于零，代入四个选项之中，得到的加速度应该为a，而满足这一条件的只有选项C符合，所以本题的答案为C。

【备考启示】有些物理问题涉及的因素众多、过程复杂，很难直接解答。但若将问题推到极端条件或特殊状态下进行分析，可以使变化关系变得明显，实现对问题的快速判断。这种将问题推到极端状态进行处理的解题方法就是极端法，极端法也可以是在题给条件下使用特殊值代入进行分析处理。高考命题导向很注重对学生思维品质的考查，恰当的应用特殊思维法参与解题过程往往能提高解题效率，使问题化难为易，化繁为简。