谈动能定理法求变力做功的命题与解题

福建 郑行军

中学物理中求变力做功的方法主要有：微元法、图象法、转换对象法、动能定理法等，不同的方法针对不同的题设特点，其中以动能定理法的运用最为广泛，题目条件的设置灵活多变，学生在求解过程中感觉类型多、思路模糊、难度较大。本文结合教学实践和考纲要求，对物理中运用动能定理法求解变力做功的题目进行整理归类，提高对此知识点的整体认知。

试题设计1：瞬间问题(位移无法求问题)

【设计思路】在瞬间问题中，受力物体与施力物体作用的时间极短，物体运动的位移无法求得，因此在试题编制中往往会关联物体运动的始末速度做题设条件，以动能为切入点，运用动能定理求解。

【例1】一个质量为0.2 kg的弹性小球，在光滑水平面上以6 m/s的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后的速度大小为4 m/s，设碰撞前后小球动量变化量的大小为Δp，碰撞过程中墙对小球做功的大小为W，则

( )

A.Δp=0.4 kg·m/s，W=5.2 J

B.Δp=0.4 kg·m/s，W=2 J

C.Δp=2 kg·m/s，W=5.2 J

D.Δp=2 kg·m/s，W=2 J

【答案】D

【点评】动能只与速度大小有关，与方向无关，墙对球的作用力为变力，且作用时间极短，位移无法求得，可利用动能定理间接求得变力做功。

试题设计2：关联力与速度关系问题(如F=kv等)

【设计思路】题设条件中作用在物体上的外力与速度存在一定的定量关系，为变力，由于速度约束，物体的运动最终往往会呈现稳定或临界状态，因此命题设计需要学生对物体的运动过程进行动态分析，求出最终稳定时物体的速度，而后应用动能定理求出变力做功。

【例2】如图1，穿在足够长的水平直杆上质量为m的小球开始时静止。现对小球沿杆方向施加恒力F0，垂直于杆方向施加竖直向上的力F，且F的大小始终与小球的速度成正比，即F=kv(图中未标出)。已知小球与杆间的动摩擦因数为μ，且F0>μmg，小球由静止到最终速度稳定时运动的位移为s，则

( )

图1

A.小球先做加速度减小的加速运动，后做加速度增大的减速运动直到静止

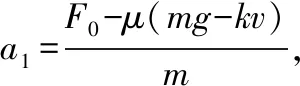
【答案】BD

【点评】竖直方向的力与速度相关，使得水平方向的摩擦力为变力，对套球进行动态分析，判断小球最终稳定的可能情况，利用动能定理求克服摩擦力做功，本题解题的关键在于对球的动态分析及动能定理等相关知识的应用。

试题设计3：斜拉牵引模型中的拉力为变力，且存在关联速度问题(F无法求问题)

【设计思路】以挂点为连接点设计的斜拉牵引模型中，在未知绳或杆的作用力时往往为变力无法直接求解，在习题命制的条件信息中一般会给出约束型物体的速度，当物体间的速度方向与绳或杆不共线时，应用运动的合成与分解分析出物体间的速度关系，可求出受力物体的速度大小，后应用动能定理求解。

【例3】某港口利用如图2所示的滑轮组转动装置来提升货物，开始时货物放置于地面，牵引车位于定滑轮的正下方A处，定滑轮离地的高度H=20 m，货物与车均可视为质点，且滑轮直径远小于H，不计一切摩擦。牵引车由A处匀速行驶到B处，速度v=5 m/s，绳BO与水平方向的夹角为53°，由于绕在轮上细钢丝绳的拉动，货物由地面从静止开始向上运动。已知货物的质量m=800 kg，则车从A运动到B的过程中(取g=10 m/s2，sin53°=0.8)

( )

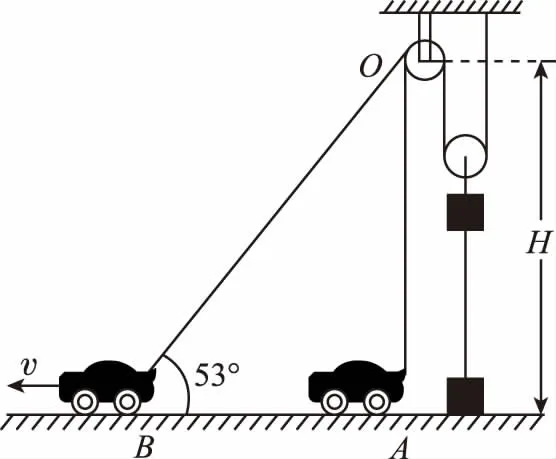
图2

A.货物最大速度为1.5 m /s

B.货物上升的高度为5 m

C.货物上升过程一直做匀加速直线运动

D.钢丝在这一过程中对货物做功为2.09×104J

【答案】AD

【点评】斜拉牵引模型中若拉力为变力，且关联速度时，可利用运动的合成与分解将物体的速度沿平行绳子和垂直绳子方向正交分解，而后利用动能定理求得两物体之间相互作用力做的功。

试题设计4：圆周运动类问题(如变轨问题)

【设计思路】圆周运动类的变力做功问题命题设计主要偏向于变速圆周运动的同轨模型和变速圆周运动的变轨模型，习题的典型特征有：①运动过程轨迹为圆或始末状态稳定且轨迹为圆；②外力大小变化呈现一定的无规则性；③条件中显含或隐含始末速度。分析的要点可由牛顿运动定律寻出始末位置的速率与力的关系，综合联立动能定理求解变力做功。

【例4】如图3所示，一质量为m的小球用两根不可伸长的轻绳a、b连接，两轻绳的另一端在竖直杆的A、B两点上，当两轻绳伸直时，a绳与杆的夹角为30°，b绳水平，已知a绳长为2L，当竖直杆以自己为轴转动，角速度ω从零开始缓慢增大过程中(不同ω对应的轨迹可当成稳定的圆周运动轨迹)，则下列说法正确的是

( )

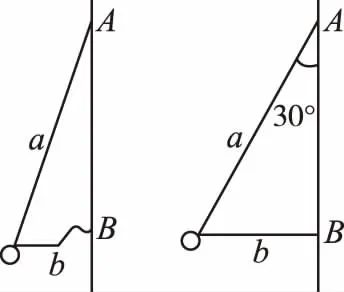
图3

A.从开始至b绳伸直但不提供拉力时，绳a对小球做功为0

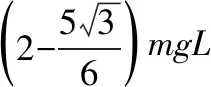
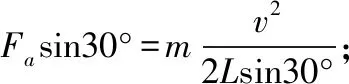
【答案】BC

试题设计5：功率恒定(牵引力为变力)，讨论位移与时间关系问题

【设计思路】恒定功率牵引习题主要以汽车两类启动为基本试题原型，运动模型有水平面、竖直面、斜面和曲面，研究对象可拓展至滑块、板等理想模型或实体模型，因此把握试题的一般性特征是此类题解题的关键。习题编制的特征有：①外力牵引受力物体时功率恒定，外力为变力；②题设条件显含或隐含始末速度大小；③关联位移、时间等运动参量。在讨论位移和时间关系时，动能定理是解题的切入点。

【例5】某实验小组设计了一种装置用于提升货物，如图4所示，在水平面上固定一竖直杆，一绷紧的轻质缆绳通过无摩擦的小定滑轮O与在高处的电动机相连，另一端和套在竖直杆上的质量为m的货物连接，开始时货物静止在杆底端的A点。某时刻电动机以恒定的功率P卷动缆绳，拉着货物沿杆由A运动到B，已知货物运动到B点的速度大小为v，此时缆绳与竖直杆的夹角为θ，货物上升的高度为h，货物与竖直杆间的摩擦力可视为不变恒为f，则下述说法正确的是

( )

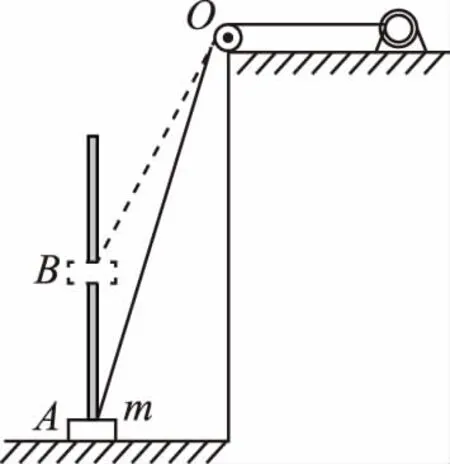
图4

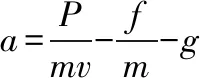
D.从A到B过程中货物所受合力的大小和方向都在变化

【答案】BC

【点评】当牵引力以恒定功率牵引时(牵引力为变力)，若要讨论位移与时间关系可利用动能定理求解。本题可由恒定功率和速度关系求出缆绳拉力；由牛顿第二定律求出货物的加速度；根据动能定理求出货物运动的时间。