构建思维模型突破化学平衡有关压强的计算
2019-04-24福建林耀昆
福建 林耀昆
一、问题的提出
近几年高考的理综化学试题以课程标准和《考试大纲》为本,考查考生的知识理解能力和知识迁移创新能力,体现了素养立意的命题思想。笔者对近几年高考理综化学试题化学平衡中有关压强计算的考查进行统计和梳理(表1),以供学习参考。
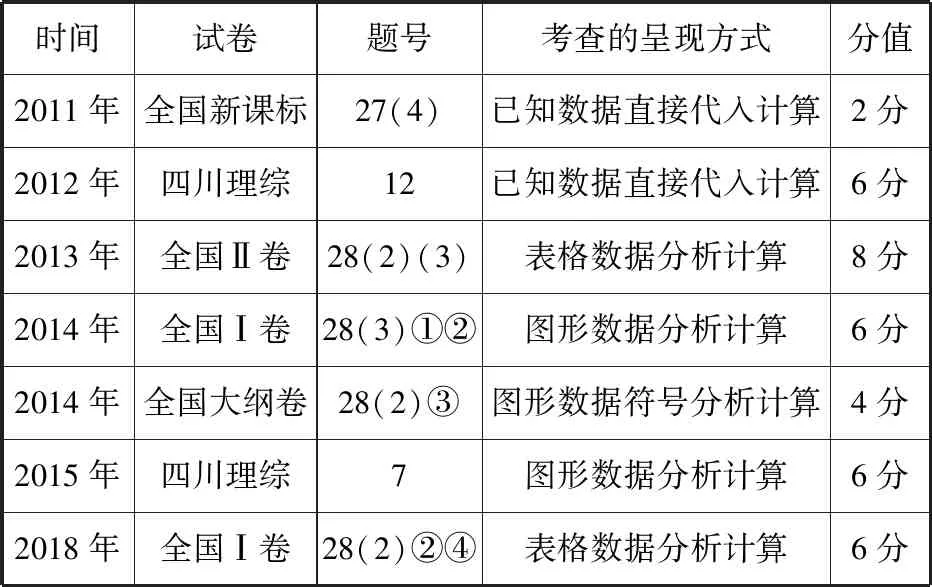
表1
从表1的“考查的呈现方式”可以看出,有关化学平衡常数及转化率的计算的考查也已从简单用已知数据的代入计算提升到采用图表形式结合压强的分析代入计算。据统计,福建理科考生在2018年全国理综Ⅰ卷第28(2)题的第②小题两个计算的得分率分别约为0.07和0.06,而第④小题得分率约为0.007。看到这么低的得分率,笔者一直在思考,在高考二轮专题难点突破的复习时,我们应该怎样帮助学生构建思维模型,有效突破化学平衡有关压强的计算。本文将从试题特征、知识梳理和提升、思维模型的构建及相应改编的高考试题进行分析,帮助学生快速解决化学平衡有关压强的计算。
二、化学平衡有关压强的计算思维模型的构建
1.试题特征
在可逆反应的起始状态或达到平衡状态时通过图表的形式提供压强的具体数值或压强数值的变化情况,要求考生在相对简单或较复杂的情境下,分析反应,利用知识迁移,采用合适的计算方法进行有关化学平衡常数或转化率的计算。
2.知识梳理和提升
化学平衡中有关压强的计算试题的核心是压强。而高中日常教学由于学生的知识经验不足及《考试大纲》没有明确要求要考查压强的计算,大多数的一线教师只是在遇到相应的练习时才会结合题目的信息给学生简单介绍压强的一些知识。笔者认为在高考二轮专题难点突破的复习时有必要对压强相关知识进行梳理和提升。主要从以下三个方面进行提升:
(1)理想气体的状态方程:pV=nRT
理想气体指的是:气体分子本身体积极小或气体分子间引力极小。真实的气体分子本身有体积,分子之间有引力,但在较高温度(不低于0℃)、较低压力(如不高于101.3 kPa)的情况下,这两个因素都可以忽略不计,用该公式计算的结果能接近实际情况。

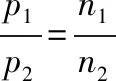
(2)分压定律:
1801年,约翰·道尔顿总结了大量实验数据,提出混合气体分压定律:在温度和体积恒定时混合气体的总压力等于各组分气体分压之和;某组分气体分压的大小和它在气体混合物中的体积分数(或物质的量分数)成正比。
即:p总=p1+p2+p3+…+pi
即:气体分压(p分)=气体总压(p总)×物质的量分数
或:气体分压(p分)=气体总压(p总)×体积分数

3.构建思维模型
首先从题目中已知数据,如“开始或平衡时的气体的总压强”、“开始或平衡时气体物质的量”或“开始或平衡时气体的体积分数”等入手,选择“三段式法”或“差量法”等合适的计算方法,在相对简单或较复杂的情境下将“气体的压强与物质的量”或“气体的压强与体积”进行知识的迁移和应用,最后代入计算并得到正确的答案。思维模型如图1所示:

该解题思维最难的是在复杂的情境下进行知识的迁移。建构主义认为,知识的迁移就是在新的情境中应用知识,在新条件下对知识的进一步学习,对知识的深入理解。在复习过程中教师要选取不同试题情境,让学生分析不同物质物质的量和压强之间的联系,要善于引导学生从气体物质的量或体积的代入计算迁移到压强的代入计算。
三、典型例题分析
例1(2012·四川·改编)在体积恒定的密闭容器中,一定量的SO2与1.100 mol O2在催化剂作用下加热到600℃发生反应:

【解题思维模型分析】
1.抓已知:题目已知数据包含1.100 mol O2、气体的物质的量减少0.315 mol、气体压强为反应前的82.5%
2.选方法:由以上已知数据分析选择差量法和三段式法共同组合计算
3.用迁移:由理想气体的状态方程中的推论将气体物质的量之比迁移到气体的压强之比
4.代计算、得答案:
起始(mol)n(SO2) 1.100 0
变化(mol) 0.630 0.315 0.630 0.315
平衡(mol)n(SO2)-0.630 0.785 0.630

得n(SO2)=0.700 mol
得平衡时α(SO2)=90%


表2
回答下列问题:
(1)由总压强p和起始压强p0计算反应物A的转化率α(A)的表达式为________。
(2)用三段式列出并计算平衡时A的物质的量为mol(结果保留四位小数);反应的平衡常数K=。
(3)用总压强p和起始压强p0表示反应体系的总物质的量n总和反应物A的物质的量n(A),则n总=mol,n(A)=mol。
【解题思维模型分析】
1.抓已知:题目已知数据包含0.10 mol A、起始总压强为4.91×100 kPa、平衡时总压强为9.53×100 kPa
2.选方法:由以上已知数据分析选择三段式法进行计算
3.用迁移:由理想气体的状态方程中的推论将气体物质的量之比迁移到气体的压强之比
4.代计算:

起始(mol) 0.10 0 0
变化(mol)xxx
平衡(mol) 0.10-xxx
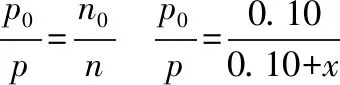
5、得答案:
(2)0.094 1 molK=1.5


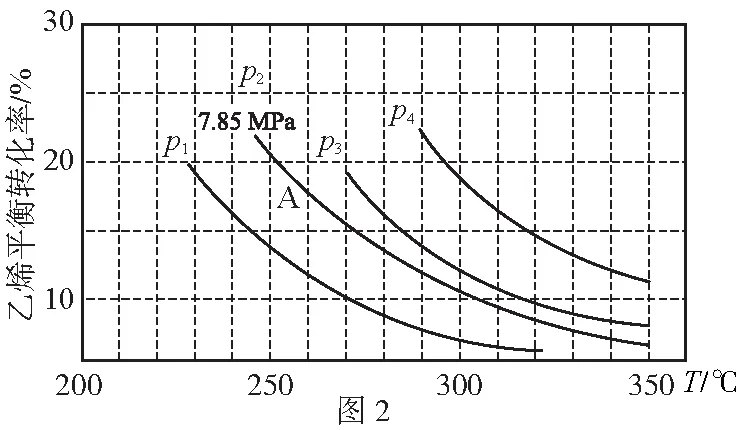
计算在图中A点对应各组分的分压及平衡常数Kp(结果保留2位小数):
p(C2H4)=MPa;p(H2O)=MPa;
p(C2H5OH)=MPa;Kp=。
【解题思维模型分析】
1.抓已知:题目已知数据包含平衡时乙烯的转化率为20%、总压强7.85 MPa
2.选方法:由以上已知数据分析选择三段式法进行计算
3.用迁移:将平衡浓度表示平衡常数迁移到平衡分压表示平衡常数
4.代计算、得答案:
设C2H4和H2O起始物质的量为1 mol

起始(mol) 1 1 0
变化(mol) 0.2 0.2 0.2
平衡(mol) 0.8 0.8 0.2
由p分=p总×物质的量分数
得到p(C2H4)=3.49 MPa
p(H2O)=3.49 MPa
p(C2H5OH)=0.87 MPa

得到Kp=0.07
例4(2018·全国卷Ⅰ·28节选)F.Daniels等曾利用测压法在刚性反应器中研究了25℃时N2O5(g)分解反应:

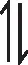
2N2O4(g)
其中NO2二聚为N2O4的反应可以迅速达到平衡。体系的总压强p随时间t的变化如下表3所示[t=∞时,N2O5(g)完全分解]:

表3
(1)研究表明,N2O5(g)分解的反应速率v=2×10-3×p(N2O5)(kPa·min-1)。t=62 min时,测得体系中p(O2)=2.9 kPa,则此时的p(N2O5)=________kPa,v=________kPa·min-1。

【解题思维模型分析】
1.抓已知:题目已知数据包含起始总压强为35.8 kPa,t=∞时N2O5(g)完全分解即平衡时总压强为63.1 kPa
2.选方法:由以上已知数据分析选择差量法和三段式法共同组合计算
3.用迁移:由理想气体的状态方程中的推论将气体物质的量之比迁移到气体的压强之比,同时也将平衡浓度表示平衡常数迁移到平衡分压表示平衡常数
4.代计算、得答案:
第(1)小题有关反应速率的计算,仍采用三段式代入

起始压强(kPa) 35.8 0
变化压强(kPa) 5.8 2.9
62 min时的压强(kPa) 30.0 2.9
答案:30.0 6.0×10-2
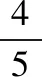

起始压强(kPa) 71.6 0
变化压强(kPa) 52.8 26.4 26.4
平衡压强(kPa) 18.8 26.4
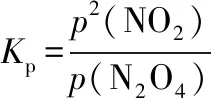
四、总结启示

