巧用等效法解一类力学动态平衡问题
2019-04-24贵州支从勇
贵州 支从勇
在高中物理人教版教材中渗透了很多物理思想和研究方法,比如说理想模型、极限思想、等效法等。而且教学大纲明确指出:“使学生受到科学方法的训练,培养学生的观察和实验能力、科学思维能力、分析问题和解决问题的能力”,总的来说,就是要培养学生的物理学科素养。因此,教师在教学过程中一定要加强对学生的物理思想的培养,要学会培养会学习的学生,而不是培养只是学习的“书呆子”。
本文主要以等效法解决一类问题为例,谈一下加强对学生的物理思想培养的重要性。等效法是研究物理现象、物理规律的一种重要方法,在教科书中很多地方都要用到等效的思想,比如“合力与分力、牛顿运动定律、运动的合成与分解”等。在解决有些物理问题时,能巧妙地应用等效法的思想,不但能使问题变得简单,还能在很快解决问题的同时发现一些意想不到的问题,从而促进学生学科素养的提高,真正达到“育人”的目的。
一、典型例题展示
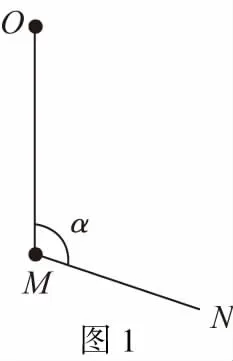
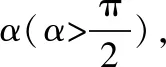
( )
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小
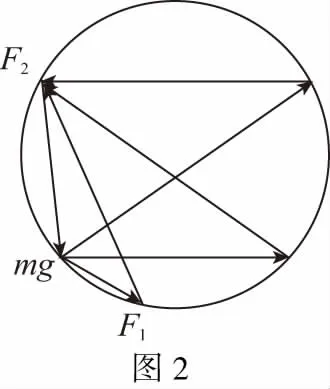
【解法一】以重物为研究对象,受重力mg、OM绳上拉力F2、MN上拉力F1,由题意知,三个力合力始终为零,矢量三角形如图2所示,F1、F2的夹角为(π-α)不变,在F2转至水平的过程中,矢量三角形在同一外接圆上,由图可知,MN上的张力F1逐渐增大,OM上的张力F2先增大后减小,所以选项A、D正确,B、C错误。
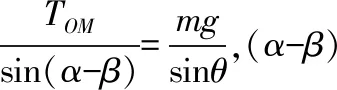
【正确答案】AD
二、解法评析
第一种方法是利用作图法,这种方法比较直观,但是对学生的要求较高,因为有两个力的方向都在变化,至少要作出三个以上不同位置的三角形,而且位置还要选择正确,才有可能看出力的变化情况,只有功底扎实的学生才能快速作出变化的图象并得出正确答案,所以,这种方法难度还是比较大的。
第二种方法主要是从理论的角度来推导,这种办法能让学生比较信服,也是多数学生喜欢采用的方法,但是这种方法对学生的数学能力要求比较高,而且花费的时间相当多,这在高考中如果花费较长的时间来解决这个问题,无疑是不可取的。
三、方法创新
从上面的解法评析可以看出,选择一种比较简单的解决这类题型的方法是很有必要的,在高中物理教材中就有这种方法——等效法。等效法的思想就是化复杂为简单,因此用等效法来解决是其中一种相对比较简单的方法。
(一)问题情境:三力平衡中有两个力的大小和方向都在变化,但是夹角不变,它们的合力的大小和方向都不变。
(二)方法探寻:这个时候如果只是关注变化的两个力,那么问题肯定就会变得复杂,如果我们对物理思想很熟悉,就会想到,物理中能让复杂的问题变简单的研究方法就是等效法,既然变化的两个力的合力不变,那么我们就可以等效为是它们的合力在变化,这样判断两个力变化就可以转化为只看一个力的变化,问题自然就变简单了。
(三)原理:根据等效替代的思想,如果有两个力的大小和方向都在变化,但是夹角不变,而它们的合力的大小和方向都不变,这个时候就可以等效为这两个力的方向不变而合力的方向在发生变化,这样就从考虑两个力的方向转变为只考虑一个力的方向发生变化,从而使问题变得简单,这也就是等效替代的作用。
(四)用等效法解决这类问题的优点:
1.用等效法的方法,可以将两个方向都变化的力转化为只有一个力的方向在变化,这不但降低了难度,而且还能直观地看出力的变化;
2.用等效法的方法,还能快速地找出极值的问题
若α=90°时,则F1、F2的最大值为mg,最小值是0;
四、应用示范
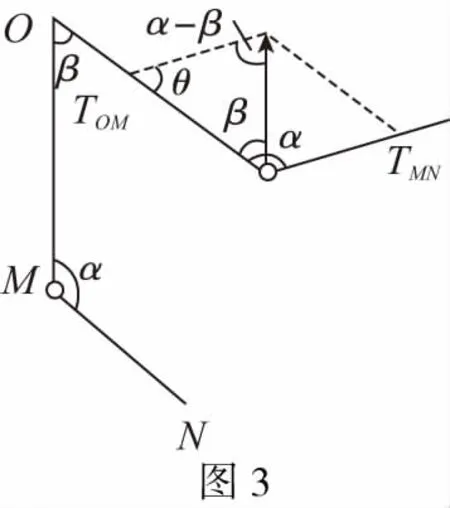
【解析】首先我们来看一下例1这道题目的要求,“现将重物向右上方缓慢拉起,并保持夹角α不变。在OM由竖直被拉到水平的过程中MN上的张力F1、OM上的张力F2如何变化。”由于是缓慢拉,所以是属于三力平衡的问题,则F1、F2的合力与重力mg等大反向,又由于拉力F1、F2的方向在变化但是夹角不变,在OM由竖直被拉到水平的过程中,OM与它们合力的方向的夹角在变大,MN与它们合力的方向的夹角在变小,此时,就可以等效为拉力F1、F2的方向不变,而合力的方向从竖直方向沿圆弧顺时针旋转到水平方向,如图4所示:
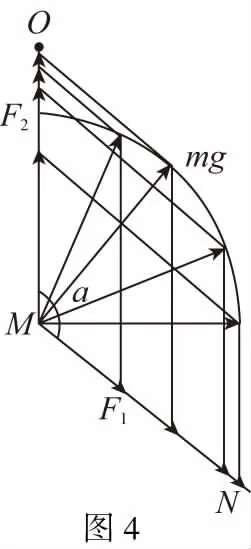
由图可知,拉力F1的大小在逐渐变大,拉力F2的大小先变大后变小。所以选项A、D正确,B、C错误。
五、变式拓展
【例2】柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N,初始时,OM竖直且MN被拉直,OM与MN之间的夹角为α=150°。现将重物向右上方缓慢拉起,并保持夹角α不变。在OM由竖直被拉到水平的过程中
( )
A.MN上的张力逐渐增大,OM上的张力先增大后减小
B.MN上的张力先增大后减小,OM上的张力逐渐增大
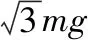
D.OM上的张力的最大值为2mg
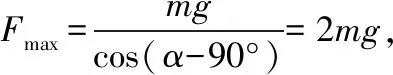
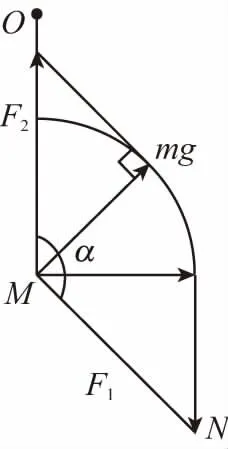
图5
【正确答案】AD
六、结束语

