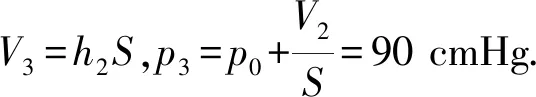分类讨论在热学解题中的应用
2019-04-24曹少平
曹少平
(湖北枝江市第一高级中学,湖北 枝江 443200)
分类讨论思想是中学物理解题中的一种重要思想方法,它一般是在原问题不能统一解决的情况下,将其分解成相互独立的若干子问题来处理,最后综合这些子问题的解答,得到对整个原问题的解答.分类讨论思想在学生的思维、推理过程中起着重要的作用,它实际上是一种化整为零、分别对待、各个击破的思维方式在物理解题中的体现.也就是说,如果被研究的问题包含多种情况,不能一概而论时,那么将确定的同一标准所研究的问题划分成若干不同的情形,并把每一种情形毫无遗漏地划分到某一类中去,再进一步讨论每一种情形的特性,得出每类情形下相应的结论,即所谓的分类讨论思想.分类讨论思想在解析中学物理热学题中有很多应用,下面结合实例谈谈分类讨论思想的应用.
1 活塞或气缸分“动”和“不动”两种情况讨论

图1
例1.如图1所示,长为2 L的圆筒状气缸可沿动摩擦因数为μ的水平地面滑动,在气缸中央有一个横截面积为S的活塞(气缸与活塞之间的摩擦不计),气缸中封闭的理想气体温度为T0,压强等于外界大气压强P0.气缸和活塞的总质量为m,在固定壁与活塞之间连有一劲度系数为k的轻弹簧(处于自然长度),现对气体缓慢加热(设气缸与地面的最大静摩擦力等于滑动摩擦力),求当气体体积变为原来的2倍时的温度.
解析:本题是热学和力学的综合题力学综合题,仔细分析可以发现,摩擦因数大小不同,会出现不同的结果.当气体受热膨胀时气缸始终静止不动是一种情形;在膨胀过程中气缸发生移动将得到另一种情形.下面分两种情况讨论.
(1) 在μmg>kL的情况下,气缸始终处于静止状态.活塞平衡条件为kL=(p-p0)S.
据理想气体状态方程有

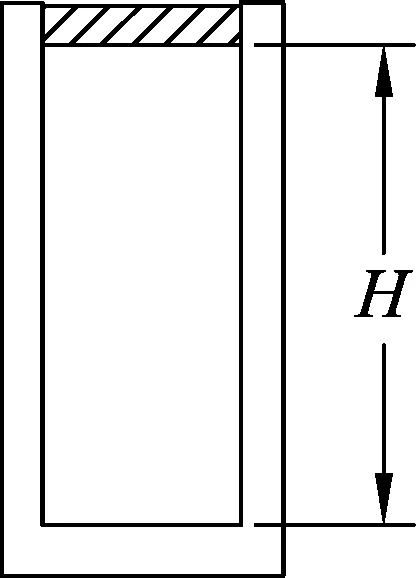
(2) 在μmg 活塞平衡条件为(p-p0)S=μmg. 阶段2.气缸发生移动后,设最终温度为T,初始状态压强p1=p0,体积V1=LS,温度为T1=T0 点评:本题的已知条件不明确,即气缸是否发生移动不明确,要求学生在求解的过程中自已补充必要的条件,然后再针对补充的不同条件进行求解.且不同的补充条件对应不同的物理情景,会产生不同的计算结果.求解本题的关键要注意分析气缸的运动过程,当温度缓慢升高时,气体的压强逐渐增大,弹簧被压缩,弹力逐渐增大.当弹簧的弹力与气缸受到地面的最大静摩擦力相等时,气缸开始向左移动,气体的压强不变.这种试题对学生的能力要求更高,要求学生有较强的分析判断能力、逻辑推理能力、物理表达能力以及创新能力. 图2 针对训练1:如图2所示,水平放置的柱形气缸内用活塞封闭一定质量的理想气体,初始温度t0=27 ℃,体积为V0=100 cm3,活塞面积为S=10 cm2.开始时容器内外压强均为p0=1.0×105Pa,已知活塞与缸壁间的最大静摩擦力为f=5.0 N,且等于滑动摩擦力. (1) 若将温度升高到t1=37 ℃时气体的体积是多少? (2)若将温度升高到t2=127 ℃时气体的体积是多少? 因为p1S 答案:(1) 100 cm3,(2) 127cm3. 图3 解析:设加热前,被密封气体的压强为p1,轻线的张力为F.因而活塞处在静止状态,对A活塞有 2poS-2pS+F=0. (1) 对B活塞有 p1S-p0S-F=0. (2) 由(1)、(2)式得 p1=p0. (3) F=0. (4) 即被密封气体的压强与大气压强相等,细线处在拉直的松驰状态.这时气体的体积 V2=2SL+SL+SL=4LS. (5) 对气体加热时,被密封气体温度缓慢升高,两活塞一起向左缓慢移动.气体体积增大,压强保持p1不变,若持续加热,此过程会一直持续到活塞向左移动的距离等于l为此,这时气体体积 V2=4SL+SL=5SL. (6) 设此时气体的温度为T2,由盖-吕萨克定律V2∝T2有 (7) 由(3)、(6)、(7)式得 (8) p2=p0. (9) 当T>T2时,活塞已无法移动,被密封气体的体积保持V2不变,气体经历一等容升压过程.当气体的温度为T时,设其压强为p,由查理定律p∝T,即有 (10) 由(8)~(10)式得 (11) 点评: 本题中对被密封的气体加热使其温度缓慢上升到T,轻线是“松驰”还是“张紧”是不确定的,因此要分两种情况讨论.能较好考查科学推理、科学论证和质疑创新等核心素养. 图4 针对训练2:如图4所示,两端开口的气缸水平固定,A、B是两个厚度不计的活塞,可在气缸内无摩擦地滑动,其面积分别为S1=20 cm2、S2=10 cm2,它们之间用一根细线连接,B通过水平细绳绕过光滑的定滑轮与质量为M=2 kg的重物C连接,静止时气缸中气体的温度T1=450 K,气缸两部分的气柱长均为L,已知大气压强p0=1×105Pa,g取10 m/s2,缸内气体可看作理想气体. (1) 求活塞静止时气缸内气体的压强; (2) 若缓慢降低气缸内气体的温度,求当活塞A、B间细线的张力刚好减为0时气缸内气体的温度. 解析: (1) 对活塞A、B整体,根据平衡条件得p1S1+p0S2=p0S1+p1S2+Mg,解得p1=1.2×105Pa. 图5 例3.如图5所示,有一个直立的气缸,气缸底到气缸口的距离为L0,用一厚度和质量不计的活塞封闭一定质量的理相想气体,平衡时活塞上表面与气缸口的距离很小(计算时可忽略不计),周围大气的压强为H0水银柱.现把盛有水银的一个瓶子放在活塞上(瓶子的质量可忽略),平衡时活塞到气缸底的距离为L.若不是把这瓶水银放在活塞上,而是把瓶内水银缓缓不断地倒在活塞上方,这时活塞向下移,压缩气体,直到活塞不再下移.求此时活塞在气缸内可能的位置以及与之相对应的条件(即题中给出量之间应满足的关系).设气体的温度不变. 解析:设整瓶水银放在活塞上后,使气缸内气体增加的压强为h水银柱,由玻意耳—马略特定律 H0L0=(H0+h)L, (1) 解得 (2) h的大小反映了水银质量的大小. 当水银注入后,活塞不再下移时,设活塞上水银的深度为ΔH,活塞下移的距离为Δx,则由玻意耳—马略特定律得 H0L0=(H0+ΔH)(L0-Δx). (3) (4) 根据水银量的多少可能发生两种情况: (1) 水银比较少,瓶内水银全部注入后,尚未灌满或刚好灌满活塞上方的气缸,这时 ΔH=h, (5) ΔH≤Δx, (6) 由(2)、(4)、(5)3式,得 Δx=L0-L, (7) 活塞距气缸底的距离 L′=L0-Δx=L, (8) 由(4)、(6)、(7)3式,得 L≥H0, (9) 即若L≥H0,则L′=L. (2) 瓶内水银比较多,当活塞上方的气缸灌满水银时,瓶内还剩有一定量的水银,这时 ΔH=Δx, (10) ΔH (11) 由(4)、(10)2式,得 Δx=L0-H0, (12) 活塞到气缸底的距离 L′=L0-Δx=H0, (13) 由(2)、(10)、(11)3式,得 L (14) 即若L 图6 点评:本题中由于水银量的不同可能会出现两种情况:一是水银量较少,当水银全部倒在活塞上方时没有水银溢出;二是水银量较多,当水银部分倒在活塞上方时就开始有水银溢出.多数考生没有注意“把盛有水银的一个瓶子放在活塞上”与“把瓶内水银缓缓不断地倒在活塞上方”的区别,不能根据水银量的多少分类讨论而出错. 针对训练3:横截面积为S=0.1 m2、高为H=1.0 m的竖直圆筒,其顶端装有一光滑紧密配合的活塞,活塞的质量和厚度均略去不计,外界大气压强为p0=75 cmHg水银柱高.现将水银缓慢注入活塞上面,活塞逐渐下降,压缩气体,直到活塞不再下移.试求:(设气体的温度不变) (1) 若水银总体积V1=4.5×104cm3时,最终筒内空气柱的高度h1; (2) 若水银总体积V2=1.5×104cm3时,最终筒内空气柱的高度h2. 解析:(1) 假设注入水银以后水银刚好从圆筒顶部溢出时,筒内空气柱的高度h0,则对于密封的气体,初态V1=HS,p1=p0;末态:V2=h0S,p2=p0+(H-h0). 根据玻意耳定律可得p1V1=p2V2, 代入数据解得h0=75 cm. 其注入水银量为V0=(H-h0)S=2.5×104cm3. 因为水银总体积V1=4.5×104cm3>V0时,最终筒内空气柱的高度h1=h0=75 cm. (2) 因为水银总体积V2=1.5×104cm3 根据玻意耳定律可得p1V1=p3V3. 代入数据解得h2=83.3 cm. 综上所述,求解热学中可能存在多种情况的试题,关键是要通过分析,正确的进行分类,且不重不漏.再根据问题分类找出相应的物理条件,然后根据条件针对不同的情况分别求解.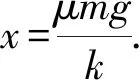
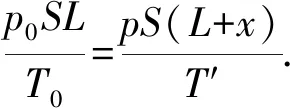







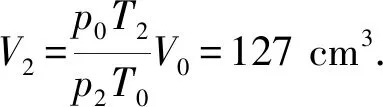
2 细线分“松驰”和“张紧”两种情况讨论





3 水银分“溢出”和“不溢出”两种情况讨论