基于真实情境的开普勒第三定律探究教学

王聿奎

(江苏省海州高级中学,江苏 连云港 222000)

1 引言

“行星的运动”是人教版物理必修2第3章万有引力定律第1节的内容．本节内容的特点是:知识容量较少,但包含的科学史料十分丰富．[1]限于教材的篇幅,知识内容和科学史料都经过提炼,非常简洁．学生在课后对学习提出相关问题:(1) 有第谷精确的观测数据作为基础,为什么开普勒发现行星运动定律用了近20年的时间?(2) 我们能通过自己的观测得出行星运动定律吗?它是否对所有天体都适用?以上问题的提出反映学生已不满足于教师的讲授和对知识的单纯识记,开始有从本质上认识规律的需要和了解知识形成过程的渴望．笔者创设探究开普勒第三定律的情景并引导学生进行科学探究,其目的,一是解决学生的学习困惑,二是解决学生进行深度学习的要求,三是使学生进一步掌握探究方法,增强探究意识,同时在探究中锻炼学生科学思维,发展学生素养．

2 探究过程的实施和引导

2.1 是否选择8大行星作为研究对象

提出设想:受课堂学习内容影响,学生提出将8大行星作为研究对象,并设想通过观测确定8大行星公转周期和半径,再根据观测结果得出开普勒第三定律．

分析引导:8大行星公转周期均较长,因探究活动的教学需求和受观测条件限制,难以实施长时间观测,同时,所选择的天体要便于观测而且要观测效果好．教师指出选择行星作为观测对象的不足并指导学生查阅太阳系天体运行相关资料以寻找新的研究对象,从运行周期和便于观测的角度选择观测对象．

问题解决:学生查阅资料后,从运行周期和便于观测的角度选择木星的卫星作为观测对象．同时还发现木星的卫星运行轨道轨道离心率小,即轨道接近圆,其亮度和大小等也适宜作为观测对象．

过程评析:学生对于全新探究情境的初期思考仍是表层的设想,也没有考虑到真实情境中的诸多影响因素,更难以形成较为完整的探究思路,容易受常识性经验的影响．因此教师要给学生指出初步设想的局限性并明确方向,而不能代替学生解决问题．学生在确定研究天体过程中已经感受到对真实情境探究的复杂性,同时,笔者还聘请本市天文爱好者协会成员帮助学生确定木星及其卫星在天空中的位置．

2.2 为什么要拍摄天体运行的照片

发现问题:设想对木星卫星观测的同时记录其在不同时刻的空间位置,通过对空间位置的数据分析获得卫星运动的周期和半径．但实际观测记录时发现:(1) 使用家用照相机和家用天文望远镜难以达到观测要求;(2) 要确定卫星位置的明显变化需要长时间的连续观测,并且轻微的震动都会影响卫星在天文望远镜中的定位格上的位置,观测的操作和记录难度很大．

探讨交流:学生在探讨交流中指出，因为卫星的时刻运动并且运动较为缓慢,因此给观测和记录造成困难．解决方案:借鉴教材中对自由落体运动的研究,采用频闪摄影的方法进行解决,拍摄卫星运动的照片并在对照片的分析中得出其运动的周期和半径．

学生使用我校省高中物理课程基地配置的视频速率CMOS显微照相机(QImaging Rolera Bolt),拍摄木星卫星运动的系列照片,如图1所示(2018年5月29日23时30分拍摄)．通过对照片的对比分析发现,如果拍摄相邻照片的时间间隔短,则照片中卫星位置的变化很小,难以进行精确处理．若时间间隔取2h左右(类似频闪频率),卫星的位置变化较为明显,因此学生以2h为时间间隔进行拍摄．

图1

过程评析:对真实情境的探究需要学生借助已有的知识和经验创造性地设计方案、解决问题．借助于频闪摄影方法,用拍摄照片代替直接观测和记录,说明学生看到问题的本质:将动态过程转化为静态问题进行解决,体现了化“动”为“静”、“动”“静”结合的思想,也体现学生思维上的创新,类比于频闪照片频率,通过照片的对比分析确定2h作为拍摄照片的时间间隔,进一步说明了学生思维能力的提升．

2.3 从拍摄的照片中能获取哪些信息

产生分歧:从对照片的分析中能获取哪些信息,学生在交流研讨中产生了分歧.有的认为照片中木星和卫星中心间的距离即表示卫星的运动半径,因此能获得卫星的运动半径;有的提出质疑,认为两者中心间的距离不能表示卫星运动的半径,只表示卫星在拍摄时刻相对木星的空间位置;有的则提出可以结合拍摄照片的时刻和卫星的空间位置确定卫星的运动周期和半径．

分析引导:照片反映的是复杂的实际问题,要以物理视角从照片中获取相关信息,是否可以从木星及其卫星的空间位置出发,通过对实际问题的简化提炼,建构物理模型,从而将实际问题转化为物理问题进行解决．

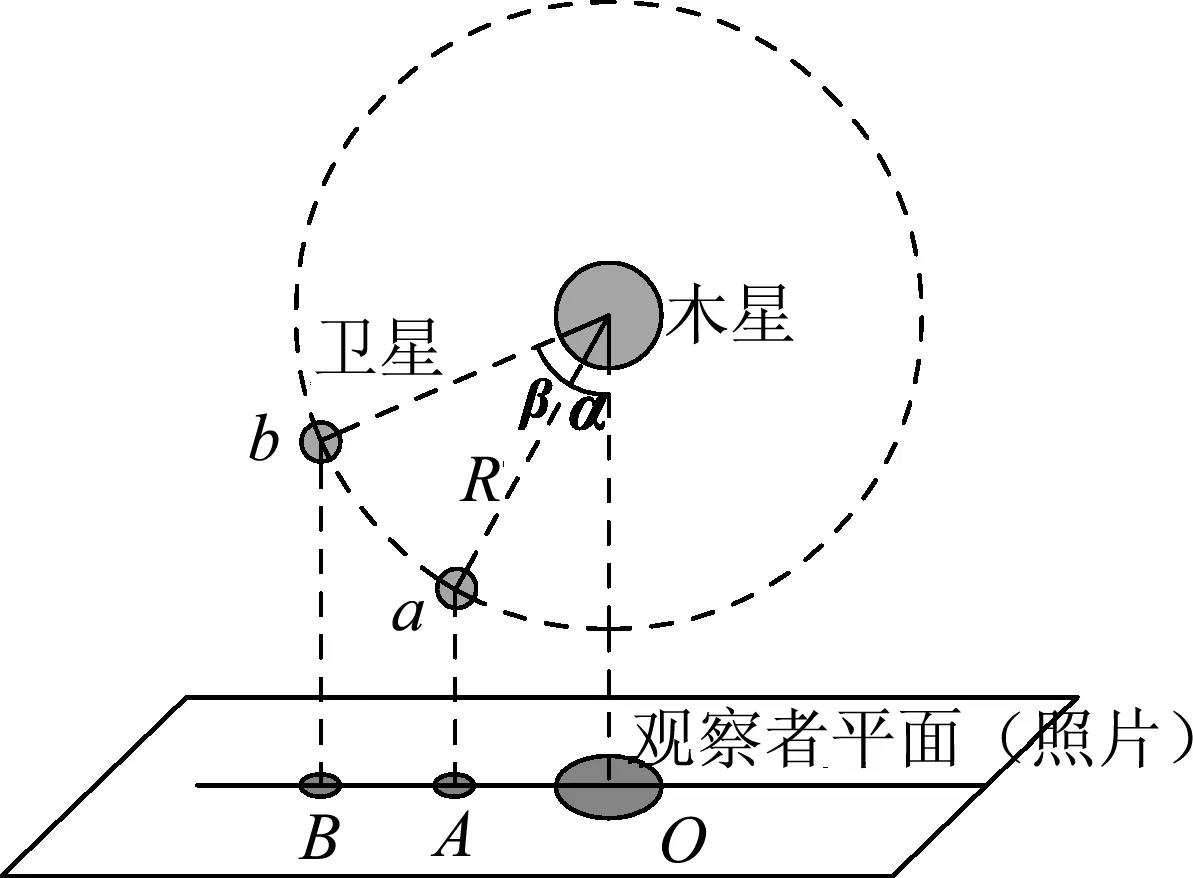
图2 木星卫星的圆周运动模型示意图

学生活动:学生重新思考照片与木星及其卫星的实际对应关系,结合在网络找到的2016年美国朱诺号探测器拍摄的木星卫星绕木星运动的真实情况的视频,将三维空间运行转化为二维平面结构,建立如图2所示的卫星圆周运行模型:认为观察者与木星和其卫星运动的轨道在同一平面内,初始时刻卫星在a位置,经一段时间到达b位置．将物理模型与数学知识相结合,解决问题并得出结论:假设卫星运动的半径为R,初始时刻木星及其卫星中心的连线与木星中心与观察者的连线夹角为α,一段时间后夹角变为β,则OA=Rsinα,OB=Rsinβ,AB=OB-OA=R(sinβ-sinα),因此照片上的距离表示卫星运动半径在观察者平面上的投影长度,照片中卫星位置的变化表示其在圆周轨道上运行时空间位置的变化．从数学的角度看,卫星的半径与角度变化(可以代表运行时间)之间存在三角函数关系．

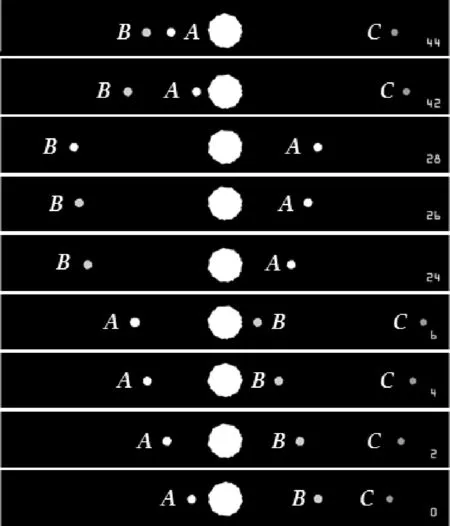
图3 木星及其卫星对齐的系列照片

同时学生提出:类比于频闪照片的处理方式,将拍摄的等时间隔的照片以木星中心为基准点对齐,按照拍摄的时间顺序依次展开(如图3所示),分析不同时刻木星及其卫星的位置关系,根据照片中卫星的大小、亮度和运行情况等因素通过推理确定同一卫星在不同照片上的位置(由近及远分别记为卫星A、卫星B、卫星C)．

过程评析:建构物理模型需要在对真实情境的分析中抓住主要因素,忽略次要因素,对情境中的信息进行简化提炼．学生从对真实视频的观察出发建立物理模型,展现了学生思维从感性上升到理性的过程．对物理模型的分析需要将物理知识、数学知识等进行综合运用,从而有效地进行问题解决．学生能够有效类比于频闪摄像方法并将拍摄的照片按照时间顺序展开,反映了学生思维上的提升和思维自觉性的增强,是学生思维的创新点之一,在交流中的质疑和评析反映了学生思维的批判性．

2.4 进行数据处理

数据记录:以木星中心为原点,木星及其卫星中心的连线建立坐标轴,取向左为正方向并测量图3中每张照片投影的长度,将测量结果记录在表1中．以时间为横轴,投影长度为纵轴建立坐标系,将表格中的点描绘在坐标系中(图4),通过描点作图法确定周期和半径的关系．

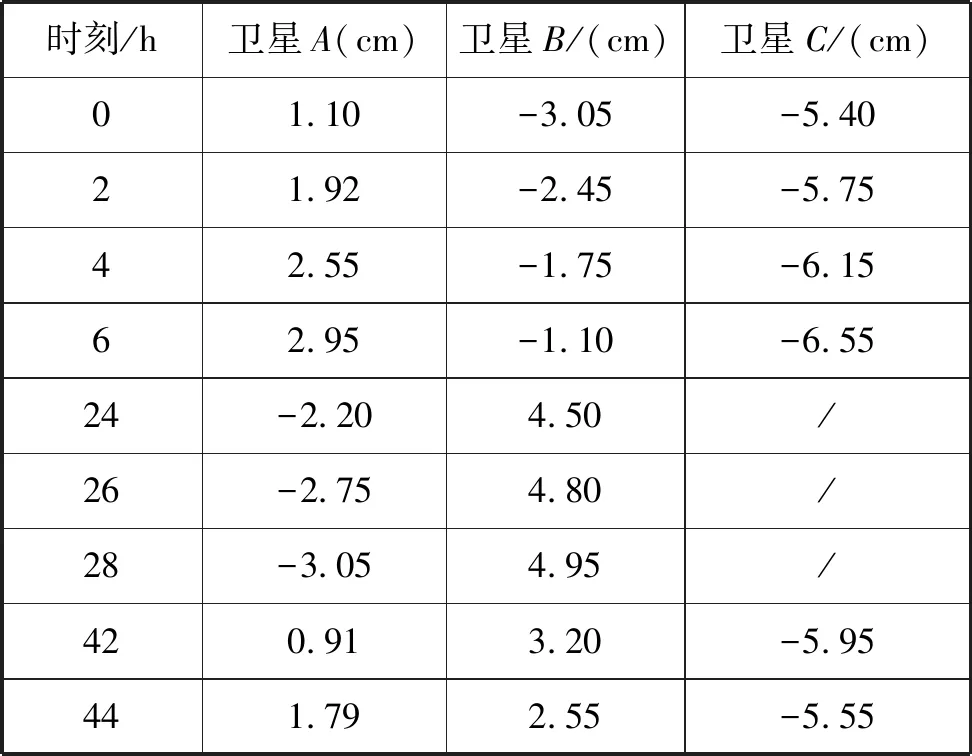
表1 照片中卫星的投影长度

分析引导:根据表格中数据描出的点比较少,难以发现规律,在前面的模型建构中已经发现卫星的半径与角度变化(运行时间)之间存在三角函数关系,因此引导学生是否可以用正余弦函数图像对所描出的点进行拟合．

寻求规律:学生在几何画板中利用正弦或余弦曲线对所描的点进行拟合,调整曲线的振幅和周期,发现拟合效果很好(如图4)．对拟合的图像进行分析:图像的振幅表示卫星运动的“半径”(如图4中rA),两波峰间的时间间隔表示卫星运动周期的一半(如图4中TA/2),由此得出3颗卫星的“半径”与周期:A卫星的半径3.2cm,周期44h;B卫星的半径5.1cm,周期88h;C卫星的半径7.9cm,周期170h．

学生同时提出借助“探究加速度与力、质量的关系”实验中选择a-m图像和a-m-1图像的方法,分别做出R-T,R-T2,R-T3,R-T1/2,R-T1/3,R-T2/3的图像从而确定卫星的“半径”和周期之间的关系．但是本探究中所得到数据较少,采用描点作图误差较大,故学生采用求比值确定卫星的运行“半径”和周期之间的关系(表2中只取2组)．

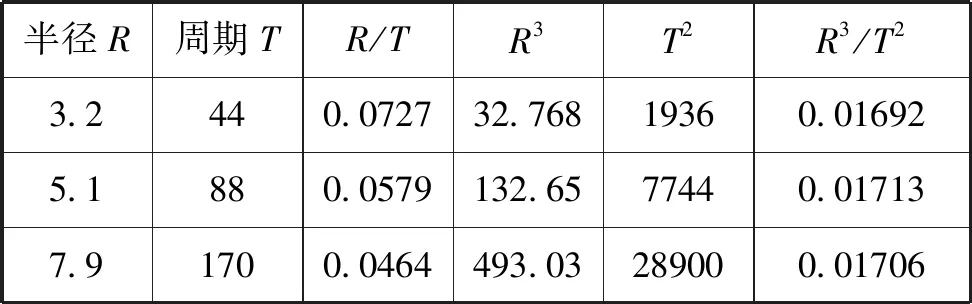
表2 探寻“半径”与周期的关系

过程评析:利用描点作图法拟合出时间和投影长度的图像再次展现了学生思维上的创新,从图像中得到卫星运动的周期和“半径”非常巧妙,使其思维得到了进一步的提升．学生能发现探究中存在数据偏少的问题并利用比值进行有效的解决,而不是一定要通过描绘出R-T关系的图像,反映了学生思维的灵活性．最终得到的探究结果足以消除学生课堂学习中的疑惑．

2.5 交流展示

学生查阅资料确定本探究中的3颗卫星分别是木卫1、木卫2和木卫3,这3颗卫星与木卫4一起被称为伽利略卫星．同时学生也通过资料了解人们对天体运动规律的认识过程:从亚里士多德的地心说到托勒密阐述了较为完整的“地心说”模型,再到哥白尼提出日心说,最后开普勒在第谷近20年的精确观测基础上发现了行星运动定律,直到1687年牛顿提出了万有引力定律,学生由此总结出了“哲学思考——数学模型——修正创立——实践检验——模型修正”的认识历程．学生将整个探究过程做成PPT在班级、校本课程和社团活动中展示交流,获得了学校师生的充分赞许．基于真实情境的探究不仅消除了课堂中存在的困惑,还使学生更深刻地理解科学的本质和发展的艰辛,了解科学探究的过程,体会科学精神、领悟科学家的思想和方法,受到科学思维方法的熏陶,[2]并在此过程中逐渐建立起科学的宇宙观和世界观．

3 教学后的反思

核心素养的落实,显然不仅仅是对教学内容的选择和变更,它更是以学习方式和教学模式的变革为保障的．[3]开普勒行星运动定律作为知识,是本节教学的载体,而知识转化为素养的重要途径就是情境,如果脱离了情境,知识就“丧失了活力和价值(余文森语)”．教师要根据教学目标、教学内容、学生特点等创设恰当的探究情境,并让学生在探究活动中逐步掌握探究方法,把握探究要素,提升探究技能,增强探究意识．

核心素养最应该聚焦的是思维素养,科学探究活动是学生发展思维的最佳途径．教师在对所创设的真实情境的探究活动中发展学生的科学思维．因此,教师对整个探究过程有整体的思考和把握,要适当地给予学生引导和指导,即不能“包办”,也不能“放羊”;真实情境中涉及的外界因素很多,因此要允许学生出现错误并进行尝试,在错误和尝试中提升思维能力．