再谈速度何处最大
2019-04-24崔延锋
物理教师 2019年4期
崔延锋
(河北省任丘市第一中学,河北 任丘 062550)

图1
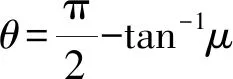
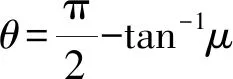
那么该问题的结论究竟如何呢?下面是笔者的一些看法.
如图1所示,切线方向上
法线(半径)方向上
又有f=μN.
得出

(1)
由x=Rθ,(1)式可得
令上式中v2=q整理得
(2)
(2)式是q关于θ的一阶线性非齐次微分方程,由高等数学知识可知,我们可以令
P(θ)=2μ,Q(θ)=2gR(cosθ-μsinθ).
则方程的通解为
(3)

(4)
(5)

(6)

(7)
(5)~(7)式得
(1-2μ2)sinθ]e2μθ.
(8)
(4)、(8)代入(3)式得,
(9)

(10)
(10)式是一个超越式,可以通过作图来找v的最大值.
我们令μ=0,μ=0.1,μ=0.2,μ=0.3,μ=0.4,μ=0.5,μ=0.6通过Excel作图可以定性找到v2-θ的图的形状如图2所示,由图可知
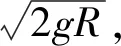

当μ超过一定数值时(例如μ=0.6)物体不能到达最低点,以上是笔者的一点看法,敬请批评指正.

图2
