水环境中高压水射流成孔的数值模拟

程树范

(西安科技大学 力学系,陕西 西安 710054)

0 引言

射流技术因其具有安全洁净的特性而被广泛应用于石油、页岩气、煤炭等燃料资源的开采[1],但由于射流成孔是一个复杂的非线性动力学过程,且涉及的影响因素较多,致使其破岩机制一直未能准确确定[2]。单纯解析描述的力度十分有限,难以解析描述复杂问题,是工程上常见的问题。采用高效的数值计算方法,基于较少假设,模拟实际射流过程也是探索射流成孔特性的一个重要途径。

由于岩石类材料的力学性质复杂,冲击成孔过程历时短暂,试验难度大,数值模拟技术作为有效的辅助手段,逐渐成为重要的研究方向。雷光宇等[3]通过对射流数值模型的分析,从岩石损伤的角度研究了高压射流成孔过程,认为射流直径和射流速度是影响成孔效果的主要因素。CHEN 等[4]采用有限元方法研究了射流成孔的速度的阈值问题,发现射流速度低于下限阈值时无法有效成孔,达到上限阈值后成孔深度不再明显增加。LIU 等[5]将光滑粒子流动力学与传统有限元方法相结合,分析了射流成孔特性,重点研究了射流角度对成孔深度的影响。除射流速度、角度因素外,王百顺等[6]研究了射流喷嘴对射流效果的影响；Stoxreiter T 等[7]则研究了围压对成孔效果的影响。

关于射流过程的数值模拟研究较多,但其研究对象多处于空气域中,而对于水环境条件下的射流研究很少涉及。笔者采用LS-DYNA 有限元显式动力分析软件建立水环境中石灰岩的水射流模型,模拟射流成孔的全过程,以论证水环境中射流成孔的可行性。分析射流速度对于成孔深度和成孔直径的影响,并重点关注射流周边岩体的应力场变化。

1 水射流模型的建立

1.1 材料的选取

准确地确定岩石材料的动态本构关系是极其困难的,但在受荷过程中岩石内部损伤劣化特性是被广泛认可的,因此选取适合于大变形、高应变率条件的岩石损伤Holmquist-Johnson-Cook(HJC)模型来模拟受冲击岩石,其相关参数如表1所示,参数的确定方法及其物理意义可参考文献[8]。同时采用屈服应力和抗拉强度均为0 的完全塑性材料来模拟射流及周边水域。

1.2 模型概况

几何模型如图1所示(周边水域没有显示),岩石尺寸为0.9 m×0.9 m×1.4 m,射流直径为5 mm,实际建立模型为几何模型的1/4,采用2 mm 标准六面体网格划分和流固耦合ALE 算法计算。同时为更加真实地模拟破岩过程,未预先施加任何接触条件,岩石边界均为无反射边界。实际工程中由于技术和成本的限制,射流速度一般不超过500 m/s,模拟的射流速度范围为200～550 m/s,速度级差控制为50 m/s,共建立了8 个数值模型进行对比。

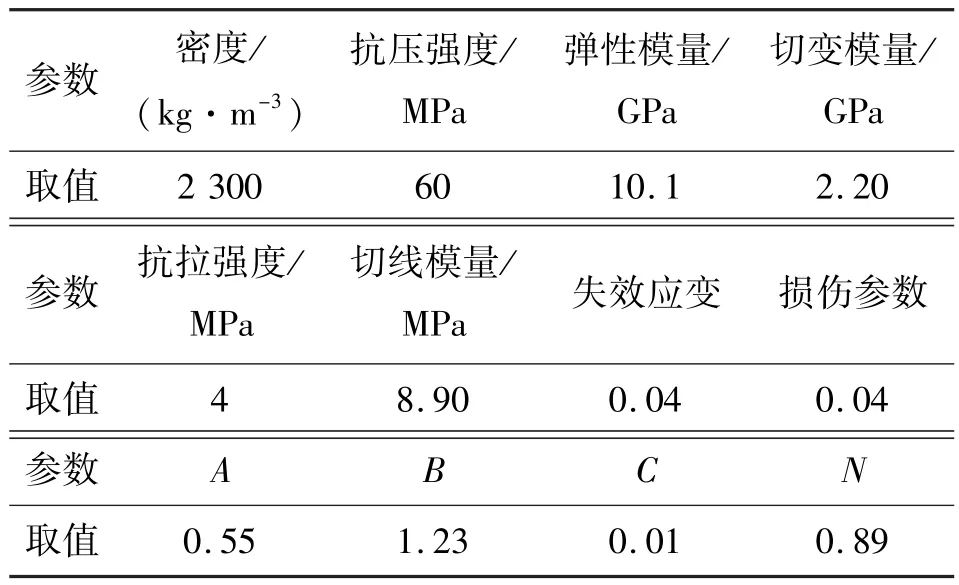
表1 石灰岩HJC模型主要参数

图1 水射流成孔数值模拟几何模型

虽然射流破岩的机制尚不明确,但无论是拉伸—水楔理论,还是密实核—劈拉理论都认为在成孔过程中岩石出现张拉破坏[2],且岩石抗拉强度较低,因此可采用抗拉强度作为失效判别条件,抗拉强度为4 MPa。

2 数值模拟结果分析

2.1 破岩过程

在高压水射流与岩石接触后,射流出现了明显的飞溅,并迅速与周边液体相融合,岩石表面出现明显的压缩变形,接触初期并未出现破坏；当接触时间达到120 μs 后,在接触区附近局部拉应力达到限值首先出现裂纹并开始延伸,可见高压射流破岩存在一个能量积蓄的过程。随后接触区岩石逐渐失去径向约束,由于泊松效应也出现拉应力,并很快达到抗拉强度,表层岩石迅速破坏,下部岩石暴露出来。在400 μs 左右形成明显的射流冲击坑,其直径约为射流直径的1.3 倍。

随着射流距离的增加,射流速度分布产生一定的变化,沿轴线向外射流速度逐渐减小,在边缘处达到最小值,从而使得射流中心区域岩石持续受压,向外逐渐转变为受拉,随着受拉区的破坏,射流中心区域原本受压的岩石开始径向膨胀,转而出现拉应力,最终也出现受拉破坏。此过程不断重复,冲击坑转变为深孔,当射流速度衰减到一定程度后,成孔过程结束。根据数值模拟的结果,整个成孔过程约为2 400～4 200 μs,与实际情况相符,射流速度为400 m/s 时的成孔过程及压力云图如图2所示,图中标尺单位经换算后为1012Pa(模型采用mm-g-μs 单位制)。

图2 射流成孔过程及压力分布云图

射流接触到岩石,实际产生的Mises 应力峰值持续稳定在700 MPa 附近,衰减较为缓慢。射流冲击过程产生的应力波主要由孔底沿着射流轴线方向传播,衰减速度快,对射流周边岩体影响较小。

2.2 成孔特性

根据数值模拟结果,可以明显看出随着射流速度的增加,成孔深度从最开始的显著增加,转变为缓慢增加,最后稳定在700 mm 左右。而射流速度对于成孔直径影响不大,实际成孔直径约为射流直径的 1.5～1.8 倍。

当射流速度为200 m/s 时岩石单元未出现破坏,即水中射流存在一个射流速度的下限阈值,当射流速度低于该阈值时无论射流持续时间多长,均无法有效成孔；当射流速度达到300 m/s 和400 m/s 时分别可以形成深度约为120 mm 的浅孔和深度达到500 mm 孔洞；随着速度继续增加,其成孔深度增加不大,500 m/s 和550 m/s 时成孔深度约为690 mm和700 mm,射流成孔深度变化不大。射流速度与成孔深度的关系如图3所示。

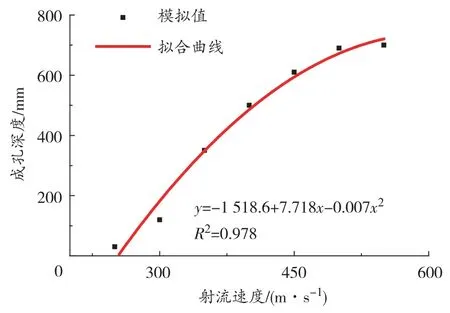
图3 射流成孔深度与射流速度的关系曲线

分析认为,当射流速度小于350 m/s 时,所成孔深度较小,实际工程价值不大；而当射流速度超过450 m/s 后,随射流速度的增加,成孔深度变化不大,经济性不理想。因此射流速度为350～450 m/s 时,综合效率最高。

采取同样的方式模拟了相同条件下空气域内初速度为400 m/s 的射流成孔,成孔孔径与水域内射流基本一致,但射流深度有所增加,约为700 mm,是水域环境下的1.4 倍。说明水环境影响了岩石从射流中吸收动能的过程,宏观上表现为射流撞击岩体完成能量交换后与周围水环境融合,并于孔中阻碍了其后高速射流与孔底的接触。

3 结论

1)在高压水射流冲击下,射流中心区岩石受压积蓄变形能,射流边界附近岩石受拉首先出现破坏,其后由于径向约束的消失,中间受压岩体向自由面膨胀,转而受拉,最终破坏。

2)射流成孔直径受射流速度的影响较小,实际成孔直径约为射流直径的1.5～1.8 倍,且沿深度方向孔径变化不大；射流速度对成孔深度的影响则较大,随着射流速度的增加,从最开始的显著增加,转变为缓慢增加,最后趋于稳定。

3)由于高压射流撞击岩体完成能量交换后与周围水环境融合,并于孔中阻碍了其后高速射流与孔底的接触,射流成孔的深度受到极大限制。