储液容器地震易损性参数计算
2019-04-22叶逊敏张征明
叶逊敏,张征明,万 力
(清华大学 核能与新能源技术研究院,先进核能技术协同创新中心, 先进反应堆工程与安全教育部重点实验室,北京 100084)
福岛核事故表明,地震是必须评价的重要外部事件之一。在福岛核事故后,我国对运行核电厂及其他核设施进行了检查,并要求开展外部事件对核电厂的影响评价。针对核电厂在超越设计基准的地震下的安全评价方法,通常分为两种:地震概率风险评估(seismic probabilistic risk assessment, SPRA)方法和抗震裕度评估(seismic margin assessment, SMA)方法[1]。通过地震易损性分析得到设备的高置信度低失效概率(high confidence of low probability of failure, HCLPF)值是SMA方法和SPRA方法中的一个重要环节[2-3]。本文介绍美国电力研究院的易损性研究方法,并将其应用在储液容器应急补水箱(ASG水箱)上,得到其地震易损性相关参数。
1 易损性方法与模型
设备的地震易损性的定义是在一个给定的地面峰值加速度(peak ground acceleration, PGA)下,设备失效的条件概率[4]。在设备失效的评估中,会有各种随机性与不确定性,影响到抗震能力的评估,进而影响对该设备能承受的最大地震动的估计。因此在易损性研究方法中,用多条不同置信度、有各自的中值和随机性的易损性曲线组来表示一个设备的易损性。一个特定失效模式的易损性曲线组,可通过能承受的地面峰值加速度中值(Am)和两个随机变量(εr与εu)表示:
A=Amεrεu
(1)
其中,εr和εu为两个中值为1的随机变量,分别表示抗震能力的内在随机性(偶然不确定性)与知识不确定性(认知不确定性)。εr和εu两个随机变量在该模型中均为对数正态分布,对数标准差分别表示为βr和βu。
通常将设备在95%置信度的易损性曲线上对应具有5%失效概率的抗震能力值称为HCLPF值,公式为:
AHCLPF=Amexp[-1.65(βr+βu)]
(2)
为得出设备的HCLPF值,需确定设备的各项易损性参数Am、βr、βu,即中值随机性。在实际计算中,为了方便,通常引入安全因子(F)的概念[5]。设备的抗震能力值可定义为:
A=FASSE
(3)
其中:F为设备真实抗震能力与安全停堆地震(SSE)引起的响应的比值;ASSE为SSE的地面峰值加速度。根据安全因子的定义,可将安全因子表示为两个有实际意义的因子:能力因子FC和响应因子FR。
F=FCFR
(4)
抗震能力的中值Am可用安全因子中值Fm表示:
Am=FmASSE
(5)
对于设备,响应因子可分为设备响应因子FRE和结构响应因子FRS,安全因子可表示为:
F=FCFREFRS
(6)
其中,能力因子FC表示设备不能正常运行的加速度水平和设计地震水平的加速度比,可通过强度因子FS和延性因子Fμ来计算:
FC=FSFμ
(7)
强度因子FS的计算公式[4]为:
FS=(S-PN)/(PT-PN)
(8)
其中:S为特定的失效模式下结构的强度,与失效模式相关;PN为正常工况载荷;PT为地震工况下设备的总载荷,即SSE下地震载荷与正常运行载荷的和。
延性因子Fμ是延性比μ的函数,延性因子描述了在地震的作用下,设备进入塑性,会吸收一部分能量,从而保持其功能的能力。在脆性失效和功能性失效的失效模式中,Fμ的中值为1。
响应因子FR可分为结构响应因子FRS和设备响应因子FRE,其中FRS是由于设备支撑处的结构响应计算中,许多参数是随机的,有较大的变化范围,在给定的PGA下,计算所得的响应与真实响应会有较大的区别,FRS可写为:
FRS=FSSFSDFMFMCFSCFSSI
(9)
其中:FSS为谱形状因子,描述地震响应谱形状的不确定性;FSD为阻尼因子,描述由于设计阻尼和实际阻尼的差别所带来的结构响应的不确定性;FM为建模因子,描述在建模过程中的各种假设所带来的与实际情况的差别;FMC为模态组合因子,是由于模态响应组合的方法造成的偏差;FSC为地震分量组合因子,是由于对地震分量组合方法造成的不确定性;FSSI为由于土壤与结构相互作用造成的不确定性。
FRE反映在设计时计算的设备响应与真实的设备响应的差别,可写为:
FRE=FQDFEDFMFMCFSC
(10)
其中:FQD为鉴定方法因子;FED为阻尼比因子。
以上所提到的安全因子F通常被认为是服从对数正态分布的,因此抗震能力值A也是服从相同的分布,而A的随机性和不确定性可用各项安全因子的随机性和不确定性的平方和开方[5]表示:
(11)
(12)
2 ASG水箱易损性计算
2.1 ASG水箱结构
ASG水箱是核电厂中典型的大型薄壁储液容器,在地震情况下要求其保持结构完整性和功能性。它属于安全三级抗震1F类设备,设计压力为0.013 MPa,设计温度为70 ℃。
ASG水箱的结构主要由封头、筒体、封底、加强环组成,水箱与基础地面连接方式为螺栓连接。筒体由5层不同厚度的筒体段焊接而成,筒体厚度由下至上分别为16、12、10、8、8 mm,对应高度分别为3 000、3 000、3 000、3 000、2 600 mm,筒体外径为9 700 mm。加强环高度位置为7 893 mm,外径为9 900 mm,厚度为10 mm。ASG水箱的总体积为1 126 m3,液体标高为14 520 mm。水箱筒体与封头、封底的材料为20HR-B[6]。
本文以谱分析得出的应力计算与应力评价结果为基础,分析计算过程中各环节的随机性,进行ASG水箱的易损性计算。
2.2 ASG水箱抗震分析模型
ASG水箱属于地面立式容器结构,理论上可将液体对容器的压力分为脉冲压力Mi和对流压力Mc[7-8],如图1所示,脉冲压力与容器壁脉冲运动所引起的惯性力相关,大小正比于容器壁的加速度;对流压力是由于液体振动所引起的液动压力。Housner给出了这两种压力的简化计算模型[7],在Housner模型中,假设流体无黏、无旋、不可压缩,水平方向只考虑加速度激励方向的流体运动,仅考虑流体晃动的1阶振型。
在Housner简化模型中,得出作用于容器侧壁上的脉冲压力为:
(13)
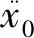
(14)
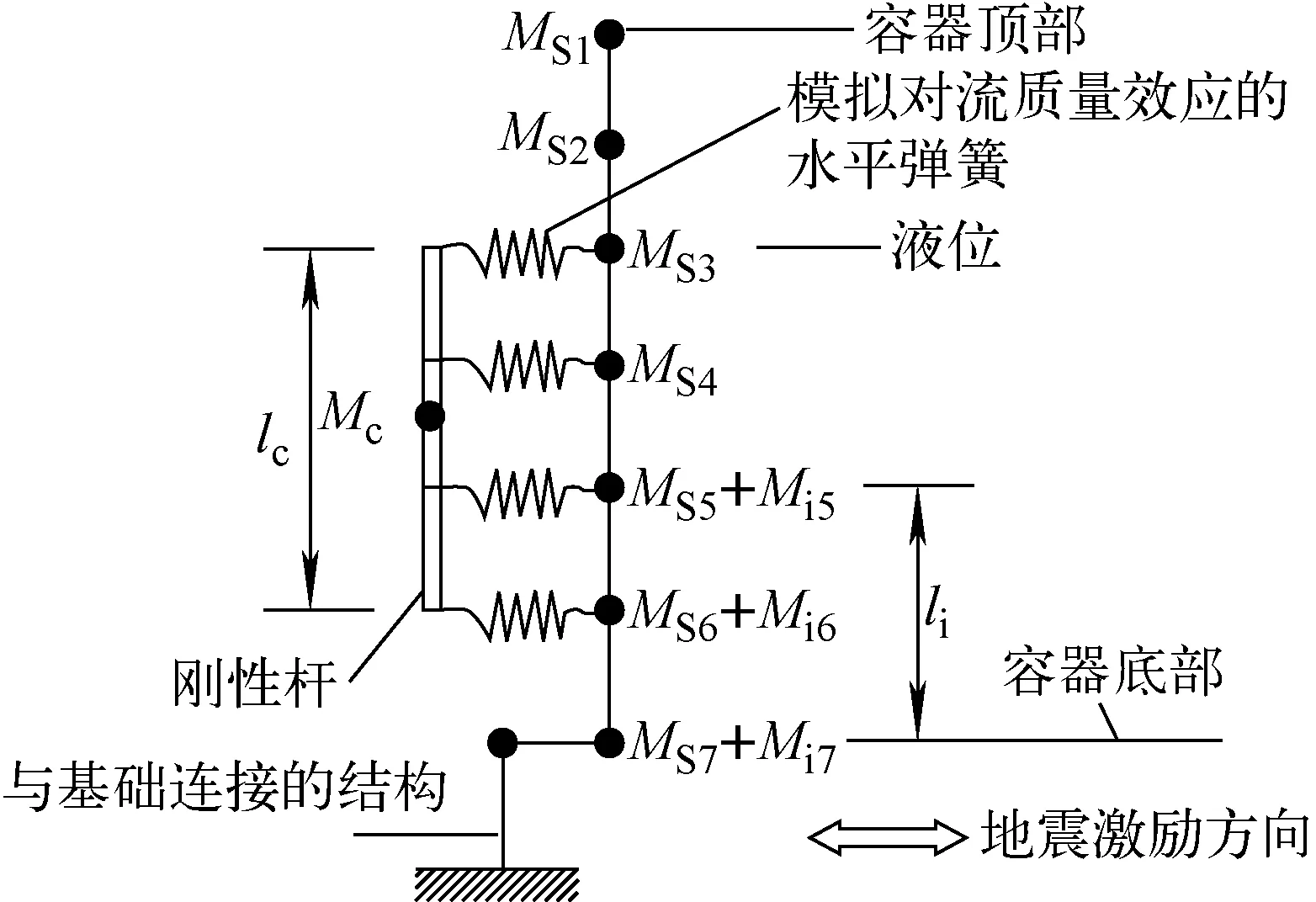
图1 柔性壁储液容器水平地震响应分析时的流体质量分布模型Fig.1 Fluid mass distribution model of flexible wall tank under horizontal seismic analysis
根据液体在侧壁上所产生的力矩,可得出Mi的高度Hi为:
Hi=3h/8
(15)
再考虑液体作用与底板上的力矩,则可将高度修改为:
(16)
由于脉冲质量与容器是同步运动的,因此在建模时,可将脉冲质量附在容器壁上。
根据对流液体在容器侧壁产生的液动压力,将其看作附着于容器侧壁的弹簧振子所产生的撞击力,则可将其等效为质量为Mc的弹簧-质量模型:
(17)
高度为Hc:
(18)
根据理论推导可知液体晃动第一频率ω[8]:
(19)
可得出弹簧-质量模型中的弹簧总刚度:
K=ω2Mc
(20)
2.3 ASG水箱结构抗震分析计算
1) 抗震分析模型
将上节中公式计算得到的参数应用到壳单元所建立的有限元模型中,如图2所示。容器径向为x方向与z方向,轴向为y方向。液体的脉冲质量通过改变筒体密度方式附加于从筒体底部到两倍质心高度的筒壁上。对流质量部分由5个分别为Mc/5的集中质量点代表,集中质量点分别通过8根弹簧与筒壁连接,集中质量点均匀分布在液面高度h至2倍于Mc质心距离的2Hc-h的5个平面内,每个平面的容器壁面均匀分布8个弹簧接触点,单个弹簧刚度为K/40,限制集中质量点Mc在y方向的位移。

图2 ASG水箱有限元模型Fig.2 FEM of ASG tank
2) 模态分析结果
模态分析得出的前两阶模态为0.301 Hz,为容器内对流质量液体的1阶固有频率。第105阶与106阶为容器1阶梁式振型,频率为7.69 Hz,第501阶与第502阶为容器2阶梁式振型,频率为18.65 Hz。其余大部分振型为容器的壳式振型。
3) 应力分析结果
采用设备所在位置SSE条件下的楼层谱进行抗震计算,用平方和开平方方法(SRSS)组合3个方向的地震响应,得到水箱的应力分布。由于ASG水箱在地震工况下失效形式主要为屈曲失效[6],因此只关注筒壁上的最大轴向压应力,计算结果显示在12 mm厚度底端和16 mm厚度底端的轴向压应力较大,容易引发屈曲失效。
设计压力在筒壁12 mm和16 mm厚度处产生的轴向拉应力分别为3.6 MPa和2.7 MPa,自重在相应部位引起的轴向压应力均为1 MPa。计算的危险点轴向压应力最大值分别为54.4 MPa和68.6 MPa。
2.4 ASG水箱易损性能力因子计算
1) 设备能力因子
由于设备主要失效形式为屈曲失效,按照RCC-M规范J篇[9]进行的应力评价,可用以下公式对其进行轴向压应力的评定:
(21)
其中:E为杨氏模量,中值为2.018×105MPa,1倍标准差为0.63×104MPa;t为厚度,两处危险点的中值为12 mm和16 mm、1倍标准差均为0.267 mm。在地震条件下,许用压应力还应乘以1.5的系数。考虑腐蚀裕量后,根据以上公式可得容器筒壁危险点轴向许用压应力中值分别为42.9 MPa和58.5 MPa,1倍标准差分别为1.70 MPa和2.07 MPa。
根据式(8)可计算出12 mm和16 mm壁厚处的强度因子分别为FS12=0.80和FS16=0.86。保守计算强度因子为:
Fsm=min(FS12,FS16)=0.80
(22)
在屈曲失效形式中不涉及塑性变化,因此延性因子Fμ可看作1,因此设备能力因子为:
FC=FsmFμ=0.80
(23)
在EPRI TR-103959中[3](表1),计算能力因子的随机性时,通常认为材料的许用值具有95%的可信度,其中值为1.2倍的许用值,得出的材料强度的不确定性为0.12。但这样的不确定性取值方法是在对材料特征没有具体了解时,对普遍情况所取的保守值,在本文计算中,已明确知道弹性模量E的概率分布以及厚度t的概率分布情况,并给出了许用压应力的标准差,因此可通过近似二阶矩的方法得出材料能力因子的随机性(式(24)),结果为0.02,与EPRI推荐取值比较,该值偏不保守,更能反映真实材料的特性。

表1 EPRI推荐的常见材料的强度Table 1 Strength of some common materials in EPRI
注:FEXX为焊接材料的最小规范名义拉伸强度
2) 设备响应因子
(1) 鉴定方法因子
在上述计算中,直接采用真实的失效模式和材料特性,因此鉴定方法的能力系数FQM为1,不确定性为0。
(2) 阻尼比因子


图3 水平方向输入楼层谱Fig.3 Horizontal floor spectrum
(3) 建模因子
建模的误差可用模态分析的频率误差进行评价,在EPRI的推荐中,建议取频率的1.1倍作为频率的1倍标准差,并得出频率的随机性。但在本算例中,由于立式储液容器的建模方法较多,可直接通过规范计算[11],可根据2.2节中的Housner简化模型建模计算,也可通过流固耦合的方式计算。本文使用以上3种较为通用的方法分别进行计算,并对比其结果,与直接取1.1倍频率作为1倍标准差相比,可更好地反映建模方法在频率上带来的随机性。
采用质量-弹簧简化模型、规范算法(式(25))、流固耦合模型得到的自振周期列于表2,综合此3个结果可得出1阶频率的1倍标准差为0.20 Hz,中值为7.60 Hz。建模因子的随机性可根据在输入谱上由于频率造成的误差进行计算,但在本算例中,输入谱(图3)从5.58 Hz至7.8 Hz对应的加速度没有变化,因此可认为建模在频率上带来的随机性βr=0,而建模因子的不确定性可看作βu=0.07[1]。
(25)
式中:T1为储液罐与储液耦合振动的基本自振周期,s;rc为储液罐体型系数,与高径比有关;hw为储液高度,m;l为底圈筒壁的平均半径,m;t0为罐底到储液高度1/3处的平均罐壁厚度。
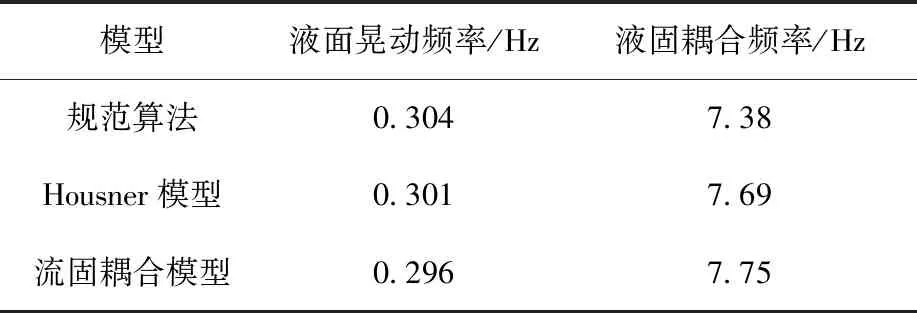
表2 不同模型频率计算结果比较Table 2 Frequency results of different models
(4) 模态组合因子
在模态分析中,筒体响应由1阶模态主导,1阶模态为7.69 Hz,2阶模态为18.65 Hz,超过1阶模态较多,可认为模态组合中没有偏离,模态组合因子为1。
根据EPRI TR-103959的推荐值,响应由1阶模态主导的模态组合的随机性βr=0.05。
(5) 地震分量组合因子
地震的分量组合通常采用100-40-40原则[10],即1个方向的100%与其余2个方向的40%组合,典型的地震分量组合造成的随机性βr=0.15[12]。
由上述分析可得出设备响应因子FRE=1.29。
设备响应因子的随机性和不确定性分别为:
(26)
(27)
3) 结构响应因子
结构响应因子中,影响较大的因子是反应谱形状因子。在对厂址谱的形状了解不透彻或未进行充分评估时,通常建议在易损性分析中采用文献[10]中值响应谱进行评估,文献[1]中也给出了结构响应因子的推荐值(表3)。
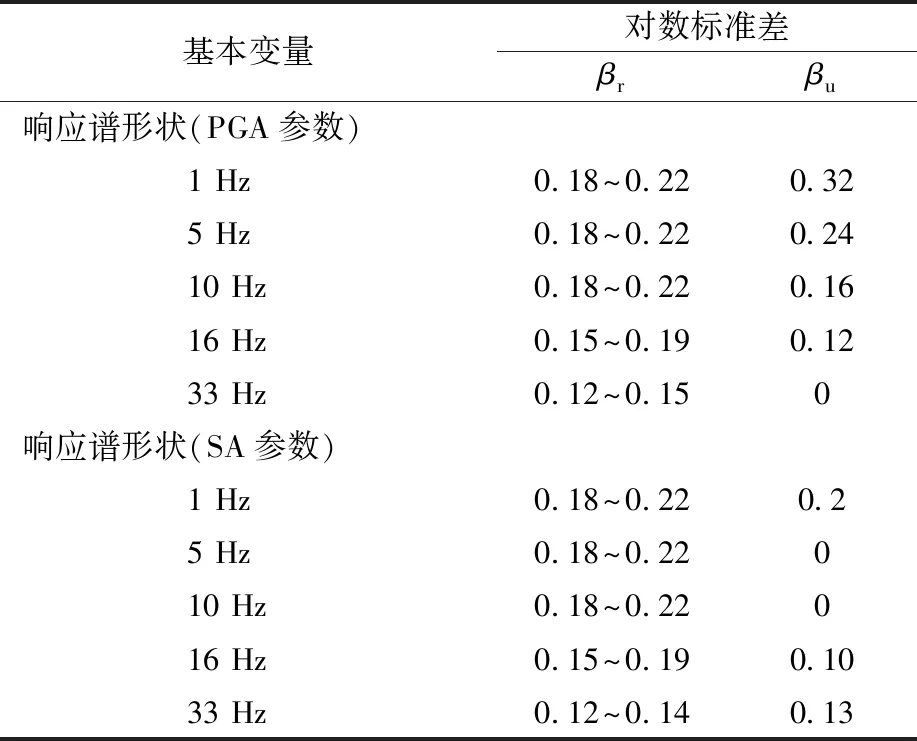
表3 EPRI推荐的谱形状因子随机性与不确定性Table 3 Randomness and uncertainty of spectrum shape factor in EPRI
但在本次计算中,采用了ASG水箱所在楼层的楼层谱作为输入,因此可直接对该楼层谱的随机性进行分析。由于楼层谱可看作各频段响应最大值的包络,具有一定的保守性。为了分析楼层谱的随机性,可将楼层谱还原为11个符合该频率谱的加速度时程,对模型分别进行时程分析,通过设备响应的统计特征值得到地震谱形状所造成的随机性。
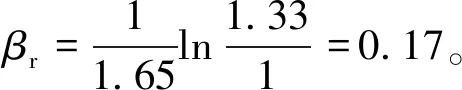
文献[1]给出的地震谱形状随机性因子βr在5 Hz到10 Hz范围内为0.18~0.22,与本文计算结果基本吻合,EPRI推荐值更偏保守,本次计算结果更能反映频率谱的随机性。
由于使用了厂址特定的反应谱进行计算,可认为不确定性较小,取βu=0.05。
由于圆形储液容器特点,当考虑两个方向峰值效应时,两个方向组合后的中值会大于中值的组合,峰值效应因子的中值可取1.09[3],可写成Fpeak=1/0.09=0.92,βr=0.1。
本次计算直接采用设备所在楼层谱,因此计算结果可认为较为接近真实情况,阻尼因子、建模因子以及模态组合因子的中值均认为是1。阻尼比因子不确定性取βu=0.15[1],模态组合因子按单个模态主导取βu=0.05[1],建模因子可认为误差较小,取βu=0.07[1]。
可得出结构响应因子FRS=0.92,βr=0.197,βu=0.10。
2.5 设备HCLPF值计算
根据以上的易损性计算,可得出ASG水箱在屈曲失效模式下的中值能力和随机性以及不确定性,亦可算出设备的HCLPF值。ASG水箱在屈曲失效的失效模式下的Fm为0.95,Am为0.19g,βr为0.25,βu为0.26,根据公式(2)可得AHCLPF为0.08g。
通过上述结果,可根据失效率定义作出ASG水箱的易损性曲线,如图4所示。
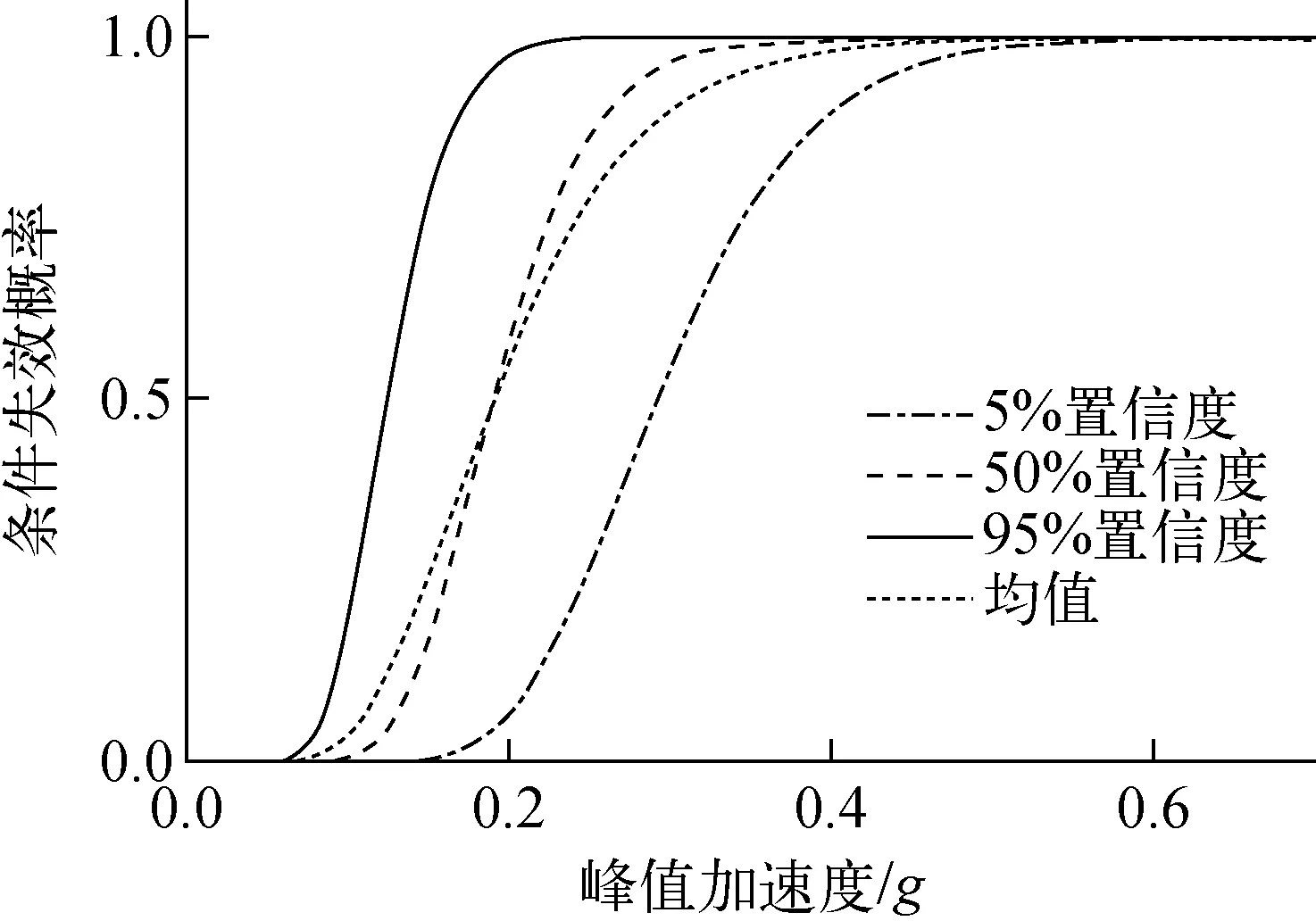
图4 ASG水箱易损性曲线Fig.4 Fragility curve of ASG tank
3 结论
本文对ASG水箱的地震易损性进行了研究,通过对其易损性参数的计算,得出其HCLPF值以及易损性曲线,对计算过程和计算结果的分析如下。
1) ASG水箱最终计算的HCLPF值为0.08g,低于SSE水平,属于抗震能力较低的设备,需在结构上进行加强。
2) 在能力因子的计算中,EPRI推荐使用1.2倍许用压应力作为强度中值。在本计算中根据实际失效形式,通过失效模式公式中各随机变量的统计特征值,得出许用轴向压应力的分布特征,并得出其随机性,更能真实反映材料强度的随机性。
3) 在建模因子的计算中,EPRI推荐使用1.1倍1阶主频率为频率的1倍标准差。在本次计算中,分别进行了两种常用的建模方式以及规范算法对频率进行计算,通过对比,可得出建模频率的中值以及标准差。
4) 在响应因子的计算中,EPRI推荐的值大多是由于对核电厂实际情况不够了解,基于均一化的地震输入谱对设备进行计算结果得到的值,较为保守。在实际工作中,通常可取得较为详细的设备所处位置的地震输入谱以及地震输入时程,通过计算其统计特征值,可较好地反映该厂址地震动的随机性,与直接使用EPRI推荐值相比,更接近真实情况。
5) 在本文的计算中对设备仅考虑了单一的屈曲失效的失效模式,在一些设备中会有危险程度相近的多种失效模式共同作用,在以后的工作中,可针对多种失效模式的联合作用,进一步进行研究。
