棒束通道中格架对传热影响的实验研究
2019-04-22干富军顾汉洋朱丽兵
干富军,刘 达,顾汉洋,朱丽兵
(1.上海核工程研究设计院有限公司,上海 200233;2.上海交通大学 核科学与工程学院,上海 200240; 3.中国核科技信息与经济研究院,北京 100037)
在压水堆燃料组件中,格架不仅能起到定位夹持作用,还能影响组件的传热从而提高安全裕度。了解格架对棒束传热的影响对反应堆燃料组件的设计非常重要。自20世纪70年代以来,众多学者针对格架对棒束传热的影响展开了广泛研究。其中最有代表性的是Yao等[1]基于文献[2-6]的实验数据而提出的格架对换热影响的经验关系式,即Nu/Nu0=1+5.55ε2exp(-0.13x/Dh),其中Nu为格架下游当地Nusselt数,Nu0为充分发展的Nusselt数,在充分发展的湍流传热中,Nu0可由Dittus-Boelter公式计算得到,ε为格架阻塞比,x/Dh为距上游格架的无量纲距离。这一关系式结构简单,对雷诺数(Re)较大情况下的格架下游传热的预测较为精确,但对于Re小于104的工况Yao公式预测较差[7-11]。Hassan等[7]对Re涵盖范围为600~2×105时格架对传热的影响进行了实验研究,发现当Re约为3 000时,格架下游最大Nu/Nu0达到极大值,随Re的增大,此值减小,当Re≥2×104时,最大Nu/Nu0几乎不再与Re相关。此外,文献[8-11]皆对不同Re时的格架传热性能进行了实验研究,并得到了相似的结论。但他们给出的最大Nu/Nu0时对应的Re的取值存在较大不同。Miller等[9]认为当Re为5 000时,此值达到最大;Kim等[10]认为Re为10 000时,Nu/Nu0达到最大值。因此,有理由认为Re并不是影响格架下游传热行为的最主要因素。在低流速加热系统中,浮升力对流动及传热的影响是不可忽略的,Huang等[12]对圆管内浮升力对传热的影响进行分析发现,即使当Re>10 000时,浮升力仍可对传热造成一定的影响。国内,关于格架对传热影响的研究多集中在超临界流体流动传热方面[13-14],较少有文献直接涉及此问题中浮升力的影响。综上所述,浮升力是否对格架下游传热存在影响有待于进一步探究。
因此,本文主要针对较低流速下格架对棒束传热的影响进行实验研究,主要研究不同参数对格架下游传热的影响。实验流量Gs为25~150 kg/(m2·s),Re约为1 000~30 000,热流密度q为25~300 kW/m2。
1 实验系统
本实验在多功能开式热工水力台架上进行,实验采用去离子水作为冷却工质。回路最大运行压力为30 MPa,流量为2.8 t/h,加热功率为1.2 MW。回路流程图如图1所示。
水箱中的去离子水经柱塞泵输运到实验支路,经过回热器及预热器加热到实验所需温度后进入实验段,加热后的水经过和来自旁通支路的冷水混合后进入换热器降温,最终进入水箱完成循环。

图1 实验台架流程图Fig.1 Flow diagram of test facility
本实验段为长约3 m的5×5正方形排列的棒束,加热管外径10 mm,壁厚0.8 mm,径距比1.33,实验本体中有2根不发热的棒,位于中心位置及1个角位,如图2所示,不发热棒外径12.9 mm。实验采用壁温滑移测量装置,竖直方向共90个等距测点,每个截面16个测点,每个格架间均布18个测点,每个测点距离25 mm。实验采用的格架形式如图2所示,格架阻塞比为0.185。
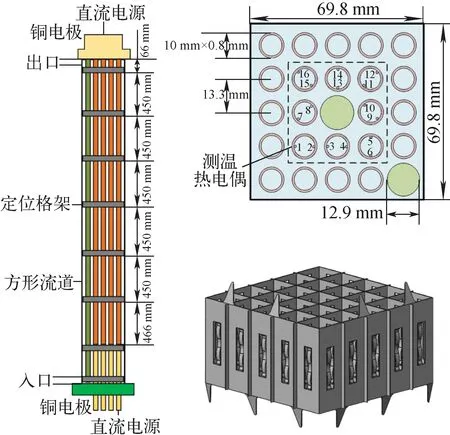
图2 实验本体及热电偶截面测点示意图Fig.2 Sketches of test section and position of thermocouple
实验中测量实验段压力、流经实验段的流量、实验段加热功率以及实验段出入口温度。为减少热损失,实验段由玻璃纤维保温材料包裹,实验热损失小于5%。
2 实验数据处理
调节阀门及加热功率,使流量、压力、入口温度及加热功率达到工况设定值,各运行参数不再变化后,依次调整热电偶测量高度,得到不同高度的内壁温测量数据。最后将实验测量得到的数据进行处理得到轴向不同高度位置的换热系数。实验局部Nusselt数的计算方法如下:
Nu(z)=α(z)Dh/λ
(1)
其中:Dh为热当量直径;λ为导热系数;α(z)为z单相换热系数。
α(z)=q/[tw,o(z)-tb(z)]
(2)
其中:q为热流密度;tw,o为外壁面温度,由测得的内壁面温度根据一维导热方法迭代求得;tb为外壁面附近流体温度,根据当地流体焓值与压力算得,当地焓值由入口焓值和测量高度根据能量平衡得到。由内壁温tw,i计算外壁温的公式如下:
(3)
其中:Do为外径;Di为内径;λw为加热棒导热系数;qv为热流密度。
基于热流密度的格拉晓夫数(Gr*)定义如下:
(4)
其中:β为膨胀系数;g为重力加速度;υ为运动黏度。
浮升力参数Bo*由Jackson等[15]提出,用于表征浮升力在对流传热中的影响,定义如下:
Bo*=Gr*/Re3.425Pr0.8
(5)
其中,Pr为普朗特数。本研究中实验Nu的不确定度为5.92%。
3 实验结果分析
图3为不同工况下格架下游的Nu分布。对于所有工况,最大Nu位于格架下游x/Dh=0,即流体刚离开格架下游位置。Nu随与上游格架位置距离的增加而减小。对于高Re工况,如Re=19 000时,Nu在0~10Dh范围内以指数形式衰减,最后在某一定值趋于稳定;对于较低Re工况,如当Re为3 500时,格架下游Nu先呈下降趋势,约在5Dh时达到最小值,此后随x/Dh的增大,Nu出现再一次上升的趋势,在10Dh时,再次呈下降趋势,最后稳定在某一定值。可见,实验工况不同,格架对下游流体传热的影响亦不同。通过图3可确定,对于所有工况,格架下游20Dh后,Nu均稳定在各自某一定值,可认为在此之后格架对下游传热的影响已很小,传热处于充分发展状态。

图3 格架下游Nu分布Fig.3 Nu distribution of spacer grid downstream

图4 格架下游归一化Nu比较Fig.4 Comparison of normalized Nu in spacer grid downstream
图4为归一化的Nusselt数(Nu/Nu0)随x/Dh的变化。由图4可发现:格架对下游传热影响的最大值随实验参数的不同而不同;格架对下游传热的影响范围随实验参数而变化;对于某些工况,最小Nu/Nu0会小于1,说明在这些范围内传热出现了弱化现象。
本实验所呈现的格架下游传热规律与之前研究[1,9]得到的结果相比具有较大不同,图5示出了具有代表性的当前实验值与Yao公式和Miller公式计算值的比较。Miller公式体现了Re在格架对棒束传热影响研究中的作用,如式(6)所示:
Nu/Nu0=1+465.4ε2·
exp(-7.31×10-6Re1.15z/Dh)
(6)
可发现,在低Re下,Yao公式和Miller公式对本实验的预测均存在较大偏差,当Re较大(如Re为23 200)时,Yao公式过高估计了格架对下游传热的影响范围,同时对最大Nu/Nu0的预测值低于实验值。

图5 实验值与经验公式计算值的对比Fig.5 Comparison of test data and calculated values based on existing empirical formulas
4 新公式建立
观察实验结果可发现,在形态上不同工况参数的格架下游传热特征和阻尼振荡系统在不同阻尼时振幅的特性存在相似性。因此,借鉴阻尼振荡表达式,利用式(7)对格架下游传热进行分析。
Nu/Nu0=1+Ae-Bx/Dhcos(Cx/Dh)
(7)


图6 系数A与不同参数的关系Fig.6 Relationship between coefficient A and other parameters
为精确比较此4个参数和系数A、B、C的相关性,利用皮尔逊相关系数来量化它们的相关程度。两个变量x与y间的皮尔逊相关系数可表示如下:
(8)
式中:σx、σy为参量x、y的标准差;μx、μy分别为x、y的平均值;E为数学期望。据此得到的A、B、C与Re、Gr*、Gr*/Re2及Bo*的相关性系数列于表1。通过表1可发现,相比于其他3个无量纲参数,Bo*与实验数据的相关性最好,因此,相较于其他3个参数,Bo*可更好地用来表征此3个系数,故利用Bo*分别对系数A、B、C进行拟合,结果示于图7。

表1 系数A、B、C与不同参数的相关性系数Table 1 Correlation coefficients of coefficients A, B and C with different parameters
系数A、B、C以Bo*为参数的拟合关系式如下:Bo*<1.6×10-5时,A=15.8Bo*0.26,B=3.16×10-4Bo*-0.55,C=12.6Bo*0.2;Bo*≥1.6×10-5时,A=0.012 6Bo*-0.4,B=0.52Bo*0.16,C=12.6Bo*0.2。上述参数配合式(7)即可得到格架下游传热关系的表达式。图8为新建立公式计算结果与实验数据的对比。可发现,新建立公式可较好地还原不同浮升力参数下格架下游不同的传热特性。

图7 系数A、B、C与Bo*的拟合关系Fig.7 Fitting curves of coefficient A, B and C as Bo*

图8 实验值与新提出公式计算值的对比Fig.8 Comparison of test data and calculated values based on new developed formula
5 结论
本文对格架下游传热的特点进行了实验研究,实验参数涵盖较广,Re约为1 000~30 000,浮升力参数Bo*为2×10-7~3×10-3。研究发现,与雷诺数相比,浮升力参数对格架下游传热的影响相关性更好。在不同浮升力参数下,格架下游传热呈现不同特征,如在浮升力参数Bo*较大时,格架下游传热表现出随格架距离增大先减小后增大再减小到充分发展值的趋势;然而当浮升力参数较小时,格架下游传热类似于文献[1,9]的研究结论,即格架下游由最大Nu/Nu0呈指数形式衰减到充分发展值。
本文将实验结果和阻尼振荡进行类比,得到了新的格架下游传热经验关系式,拟合得到的公式与实验值吻合较好。此关系式不仅可很好地预测浮升力较大工况下格架下游复杂的传热形式,还适用于浮升力影响较小的工况。
