地震作用下混凝土重力坝极限抗震能力分析
2019-04-22王旭东张立翔朱兴文
王旭东,张立翔,朱兴文
(1.昆明理工大学建筑工程学院工程力学系,云南昆明650500;2.大理大学数学与计算机学院,云南大理671003)
2008年汶川发生了里氏8.0级特大地震,地震烈度Ⅺ度,地震对震区内的水电工程造成了极大的影响。不少地区地震烈度远超我国现行地震设防烈度区划图的设防水准,例如设防烈度只有Ⅷ度的紫坪铺电站在此次地震中经历了烈度近X度的考验。由此可见,地震具有极大的不确定性,重要的水工建筑物一旦造成破坏,将引发重大的次生灾害,给下游的居民的生命财产级社会经济发展带来巨大的威胁。因此进行地震作用下的混凝土重力坝极限抗震能力分析显得十分重要。
混凝土作为一种准脆性材料,在地震动荷载较小时,表现为线弹性行为,随着地震动的不断增大,混凝土发生损伤开裂,并表现出应变软化特征。目前材料非线性模型是发展最成熟的塑性损伤模型。国内外众多学者运用混凝土塑性损伤模型对混凝土重力坝在地震作用下的非线性动力响应进行了广泛的研究,并取得了一定的研究成果[2,3]。Cevera[4]运用各向同性损伤模型,对Koyna重力坝在地震作用下的损伤破坏进行分析,得出混凝土重力坝的非线性性状能够利用各向同性损伤模型来描述。丁柱等[5]根据塑性损伤模型及Mohr-Coulomb屈服准则得出重力坝的塑性损伤区。文献[6]采用混凝土塑性损伤模型,并运用两条不同峰值加速度的地震波对重力坝进行检查,得出了开裂位置及破坏过程,破坏过程可以分为滑动和翻转两个阶段。
1 混凝土塑性损伤模型
混凝土坝的破坏是从混凝土损伤开始,进而发生开裂及裂缝扩展所致。混凝土塑性损伤模型是根据Lubliner,Lee与Fenves(1998)提出的塑性损伤模型确定的,通过引入损伤因子,来反映混凝土等准脆性材料在周期性往复动荷载作用下后继屈服的损伤机理。该模型考虑了材料拉压性能下的差异,能够用于模拟静水压力下因损伤引起的材料退化,退化主要表现在混凝土的抗拉压屈服强度的差异,混凝土拉伸屈服主要表现为软化,而混凝土压缩屈服主要表现为先硬化后软化,所以混凝土的拉伸与压缩采用不同的损伤因子。本文利用该模型来模拟混凝土重力坝在地震作用下的极限抗震能力。
由塑性增量理论可知,总应变张量ε由弹性部分εe和等效塑性部分εp组成。混凝土产生塑性损伤时,通过引入损伤因子来描述混凝土的刚度退化现象,混凝土材料发生损伤后应力应变可由式(1)表示
E=(1-d)E0
(1)
式中,E0为初始弹性模量;d为刚度退化系数,再周期循环荷载作用下当混凝土由受拉转化为受压状态时,混凝土的弹性刚度会得到一定的恢复,即“单边效应”。为考虑此效应,假定损伤变量d符合下式
(1-d)=(1-Stdc)(1-Scdt)
(2)
式中,St和Sc为与应力方向有关的刚度恢复应力状态的函数,可定义为
(3)
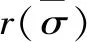
混凝土材料的塑性流为
(4)
塑性应变率根据塑性流准则计算,定义在有效应力空间的塑性势,塑性应变率按式(5)计算:
“游之”“记之”是对物象特征的记录、记忆,“悟之”则是对事物的分析、思考和概括提炼,需要去芜存精,深思熟虑,由表面而及本质,去立意,去构思,“意在笔先”“胸有成竹”如此而达到开悟的境界。
(5)
(6)
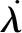
混凝土屈服面的定义为
(7)
其中,
(8)
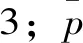
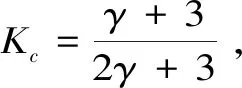
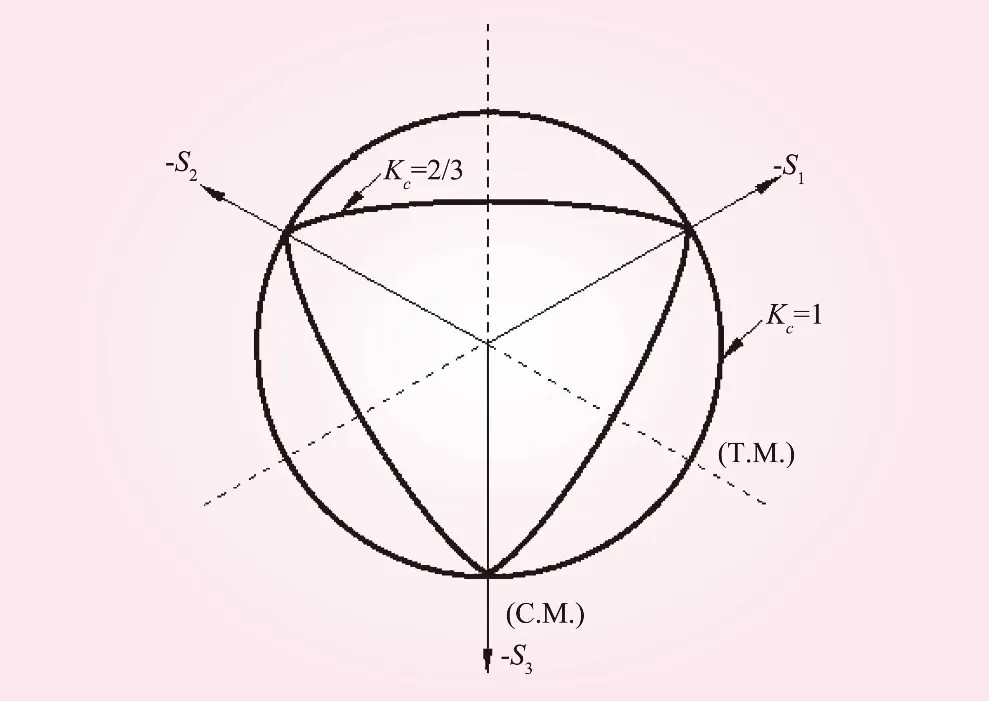
图1 混凝土在S1、S2轴上的屈服面
2 Koyna重力坝抗震能力分析验证
2.1 Koyna重力坝动力计算模型
Koyna重力坝是世界上少数几个在强震作用下有完整破坏记录的重力坝之一,是重力坝动力分析的经典研究对象。该坝段坝高103 m,坝底宽70 m,坝顶宽14.8 m,坝前水位91.75 m。该坝段于1967年12月11日遭受6.5级地震作用发生开裂,同时裂缝处产生渗漏。本文结合混凝土塑性损伤模型分析Koyna重力坝的极限抗震能力。
计算考虑了重力、静水压力、动水压力及地震荷载。混凝土弹性模量E为31 027 MPa,泊松比μ为0.2,密度ρ为2 643 kg/m3,膨胀角φ为36.31°,根据《水工建筑物抗震设计规范》[8]的规定,重力坝的阻尼比一般取0.05~0.1,本文中阻尼比取ζ1=ζ2=0.05, Rayleigh阻尼可以根据线弹性分析得到前两阶频率计算得出;动水压力按Westergaard公式考虑。地震荷载采用Koyna重力坝遭受地震时的强震记录,综合考虑了地震波的采样频率和高阶模态振动周期的影响,取时间步长为Δt=0.01 s。同时考虑水平向地震作用及竖向地震作用,加速度时程曲线如图2所示。
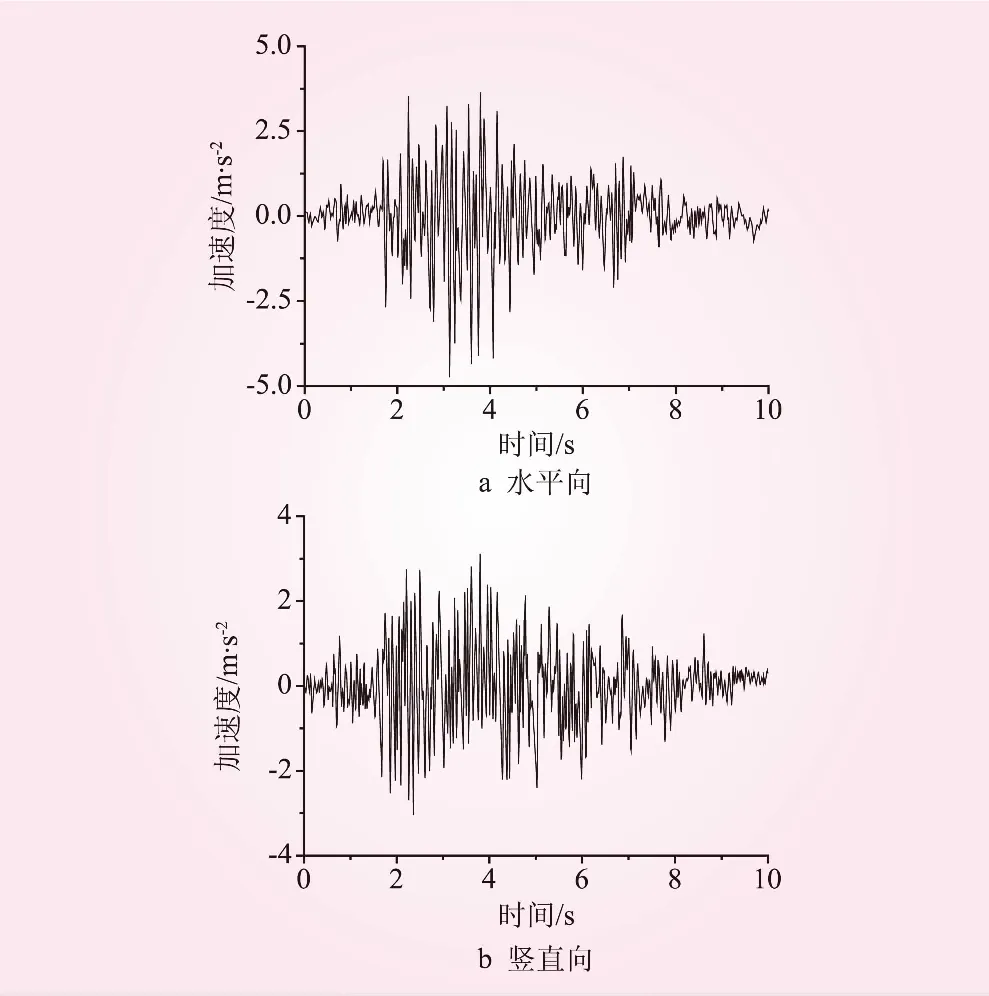
图2 水平地震加速度时程曲线
2.2 Koyna重力坝抗震响应特征分析
在地震发生之前,重力坝坝体保持弹性变形,坝体受到重力和静水压力等荷载作用,重力坝坝体没有发生损伤。当地震峰值加速度从0.1g增加至0.2g时,下游折坡处开始产生损伤,这是因为此时重力坝受弯产生拉应力引起的。当地震峰值加速度增至0.3g和0.35g时,下游折坡处损伤破坏区域累积加大,同时因为坝踵产生应力集中,坝踵处产生一些损伤;当水平地震加速度峰值增至0.4g时,坝体折坡处损伤区向上游扩展,由于此时的坝体不仅有受弯的拉应力,还有因重力引起的向下的应力,因此损伤不是水平向上游面扩展,而是向下弯曲扩展;当水平地震加速度峰值达到0.45g和0.5g时,坝体折坡处产生上下游贯穿性损伤区,坝体将产生渗漏。
如图3所示,Koyna重力坝在强地震作用下的损伤模拟结果与振动台试验的结果基本一致[9],说明采用混凝土塑性损伤模型能够很好的模拟在强震的作用下的损伤破坏过程。根据坝体产生贯穿性损伤区的破坏准则,可以认定Koyna重力坝的极限抗震能力为0.4g~0.45g。
3 某混凝土重力坝抗震能力分析
3.1 某混凝土重力坝计算模型
云南省某水电站挡水建筑物有碾压混凝土重力坝构成,该坝段坝顶高程为1 139 m,正常蓄水位1 134 m,坝高109 m。有限元计算网格如图4所示。设X轴为顺河流方向、Y轴为垂直向上方向。坝趾区地震烈度Ⅶ度,100年超越概率2%的基岩水平加速度峰值达0.229g。根据输入的地震强度等级对Koyna地震波调幅,忽略坝-基作用,假设地基为刚性。
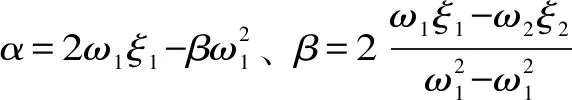
3.2 某重力坝抗震响应特征分析
图5为a=0.45g时坝顶相对地面的水平及竖直位移。坝体在地震作用的前2 s,水平位移小于15 mm,竖直位移小于10 mm。在2~4 s期间,峰值位移增加且振幅来回振荡,在振荡期间坝体结构产生损伤破坏。在t1时刻后,水平及竖直位移发生了一个大的偏移,这是由于坝体折坡处产生贯穿性损伤区,坝体头部上下摇摆造成的。
当地震峰值加速度为0.1g至0.3g时,该重力坝坝踵及折坡处产生较小损伤区,然后平稳增加。因为坝踵部位受到应力集中作用,在地震作用时,应力较高的地方通过损伤开裂进行应力转移和释放。当地震峰值加速度增加至0.35g和0.4g时,坝踵及上下游折坡处损伤区继续增大,同时应力继续释放转移,但损伤区较小,坝体主体是安全的。当地震峰值加速度达到0.45g时,坝体头部折坡处产生贯穿性损伤区,坝体整体失稳,同时坝踵,坝趾和折坡处损伤区随着地震烈度的增大而增加。当地震峰值加速度达到0.5g和0.55g时损伤区域继续扩展,尤其到0.55g时,坝趾产生由下游至上游斜向下方向的贯穿性损伤区。以坝体产生贯穿性损伤区为破坏准则,认定该重力坝极限抗震能力为0.4g~0.45g。

图3 Koyna重力坝在不同地震峰值加速度下损伤示意

图4 混凝土重力坝有限元网格
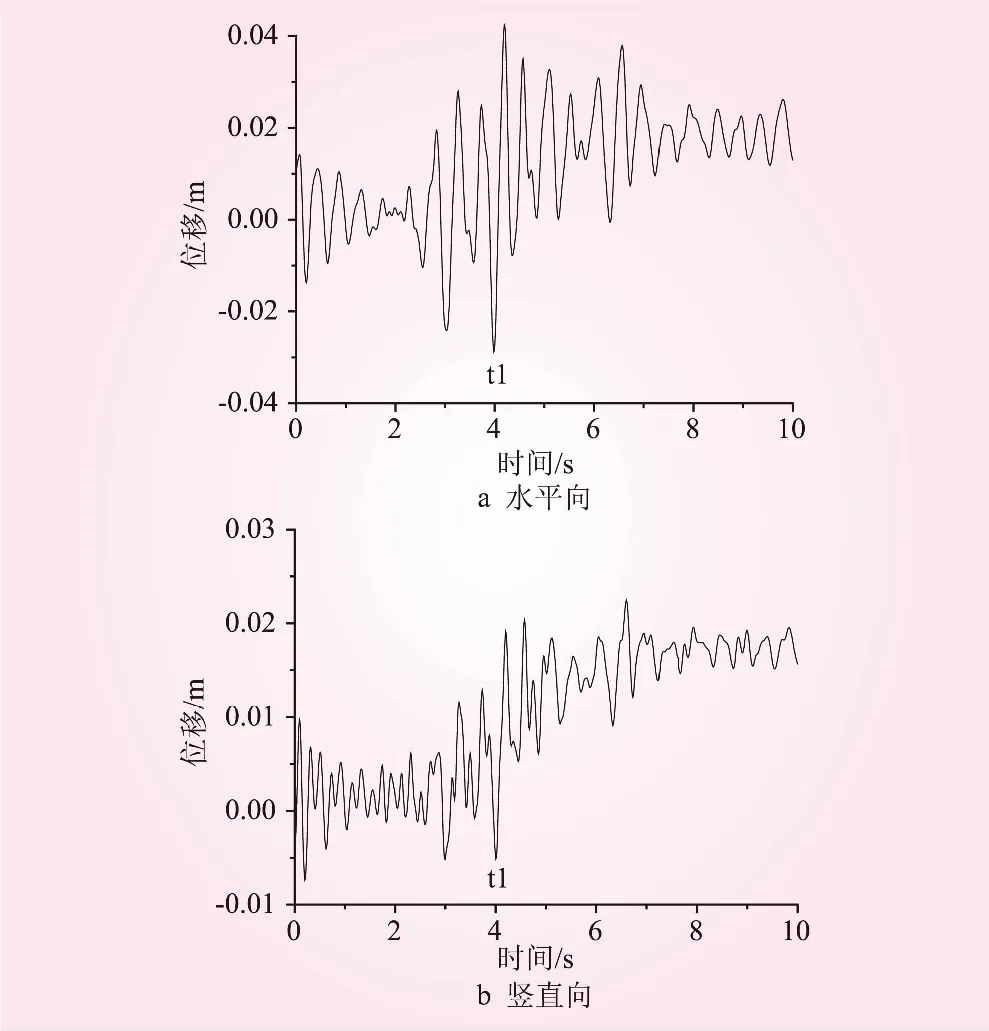
图5 a=0.45g时坝顶位移
通过Koyna坝段与该坝段比较可以发现,两坝段在地震作用下的损伤破坏区域基本相同,损伤破坏区域集中分布在坝踵及折坡处,其中坝体头部折坡处在强地震作用下容易产生近水平向的贯穿性损伤区,此位置是重力坝的抗震薄弱部位。重力坝在地震作用下的破坏是一个损伤累积演化的过程,其中取决定性作用的是拉伸损伤,而坝体拉伸损伤主要分布在坝踵区域。所以坝踵是混凝土重力坝抗震设计的重点关注部位。
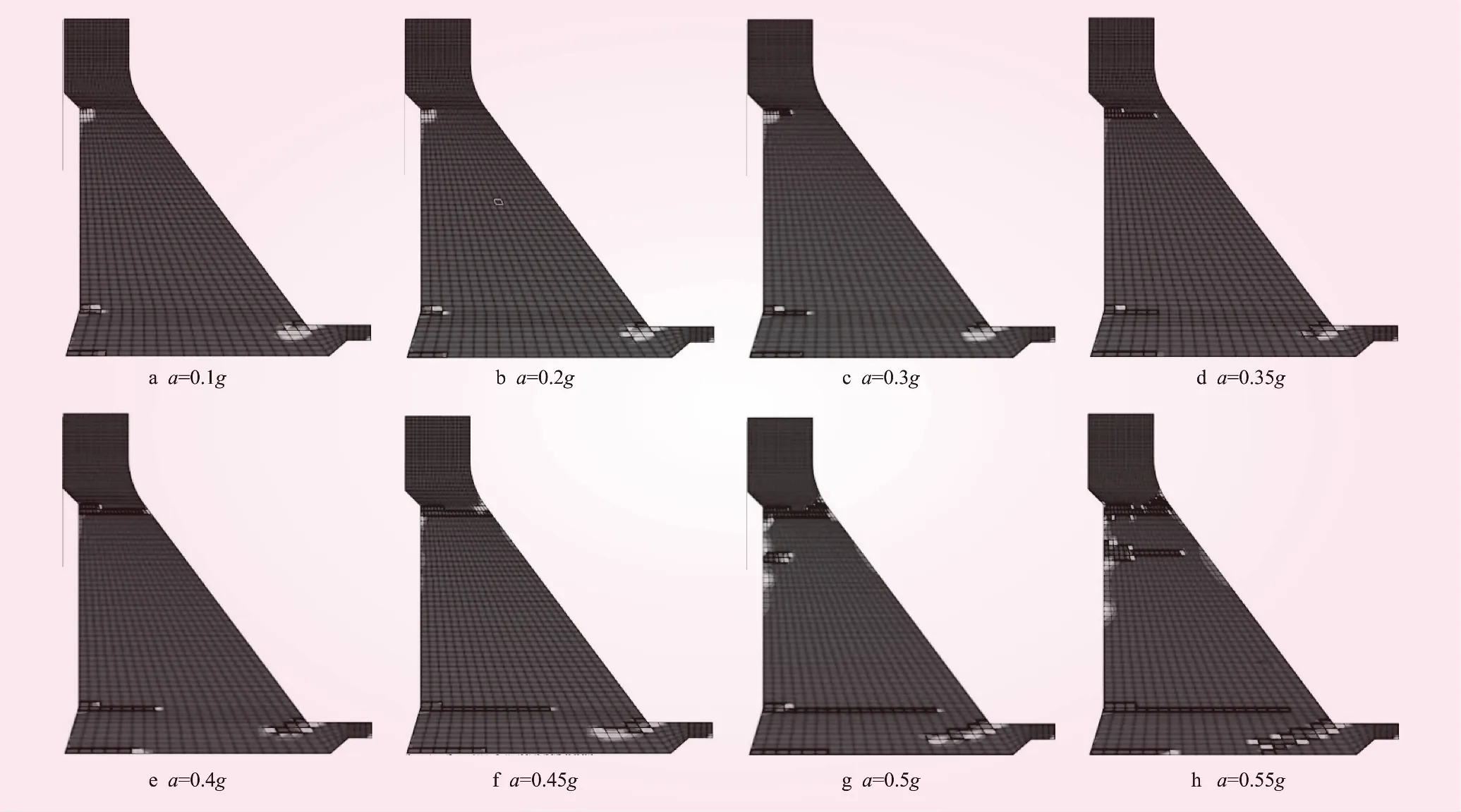
图6 某混凝土重力坝在不同地震峰值加速度下拉伸损伤示意
4 结 论
本文采用混凝土塑性损伤模型,基于坝体产生贯穿性损伤区为破坏依据,对Koyna混凝土重力坝及云南省某混凝土重力坝的极限抗震能力进行分析,通过计算得出以下结论:
(1)两个坝段在不同地震加速度下损伤破坏区域基本相似,但由于坝体尺寸不同,所以损伤破坏区域存在些许不同。损伤区域主要集中在坝踵处和坝体折坡处,因此为重力坝的坝踵及坝体折坡处为抗震薄弱区。
(2)通过两个坝段进行对比发现,当地震强度较小时,坝踵区域产生应力集中,开始产生属性损伤区,随着地震强度增大,坝踵及坝趾损伤区域继续增大,重力坝头部折坡处形成贯穿性损伤区。
(3)Koyna重力坝地震破坏形式基本与试验模型以及实际地震破坏形式相一致,所以混凝土塑性损伤模型能够真实的模拟地震作用下的混凝土重力坝的损伤破坏过程。根据破坏准则可以基本判定Koyna重力坝的极限抗震能力为0.4g~0.45g,云南省某混凝土重力坝的极限抗震能力为0.4g~0.45g。
