GM(1,1)模型的改进现状及应用

陈鹏宇，邓宏伟

（内江师范学院 地理与资源科学学院，四川 内江 641100）

0 引言

灰色系统理论由我国学者邓聚龙提出，经过不断的完善和发展已经在许多领域得到了广泛应用[1，2]。GM(1,1)模型作为灰色理论中最基本的预测模型，其建模原理简单，易于操作。但是，传统GM(1,1)模型在建模原理上存在固有缺陷，使其不具备白指数率预测无偏性[3]。正是由于该缺陷的存在，为GM(1,1)模型的改进留下了大量空间，从而涌现出了各式各样的改进算法。如果避开所谓“灰色”、“累加”等概念，从本质上讲，GM(1,1)模型属于指数函数的一种建模方法，而各式各样的改进算法无非是寻求一个最佳逼近结果或者最佳拟合函数。目前，GM(1,1)模型的改进算法繁多，各类改进算法的思路各不相同，建模的难易程度有所差异。为此，本文对GM(1,1)模型的改进现状进行了总结，对比分析了各类改进算法的优缺点，最后给出了GM(1,1)模型改进算法的应用建议。

1 GM（1，1）模型的建模原理和缺陷分析

令x(0)为GM(1,1)模型的建模原始序列：

其一次累加序列为：

定义：

为GM(1,1)模型的灰微分方程，即GM(1,1)模型的定义型。式中，a为发展系数，b为灰作用量，

以最小二乘法确定参数：

式中：

GM(1,1)模型的白化方程为：

GM(1,1)模型的时间响应式为：

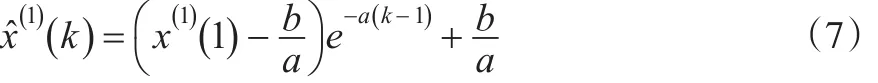
还原值为：

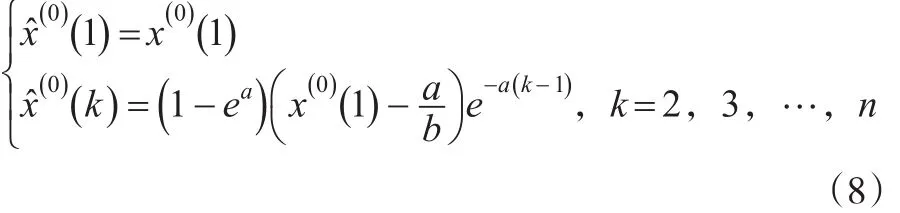
从GM(1,1)模型的拟合公式（8）可见其适合于近似齐次指数序列的建模分析。但是GM(1,1)模型不具备白指数率预测无偏性，这是由其固有缺陷导致的，具体而言就是白化方程与灰微分方程的不匹配问题，已经有许多学者从不同的视角对其进行分析，具体可见文献[4] 中的总结分析，本文不在复述。除此以外，初始条件的选择也常被认为是GM(1,1)模型一个缺陷，表现在两个方面，其一是对累加数据的拟合函数（7）默认经过了初始点，与最小二乘拟合思想不符[5]；其二是一次累加算法使得还原函数（8）对初始值不存在拟合效果[4]，所以只能默认其等于初始值，这是不合理的。

2 GM（1，1）模型的改进现状

GM(1,1)模型的固有缺陷主要是指白化方程与灰微分方程的不匹配问题及初始条件的选择问题。相对而言，初始条件对拟合精度的影响一般不及前者，其改进方法也多是添加一个初始值修正项或以最小二乘原理求解最优初值[5，6]，本文不再详述。针对白化方程与灰微分方程的不匹配问题，可以采用多种修正方法，主要总结为背景值构造的改进、白化方程参数重构、灰微分方程建模（离散GM(1,1)模型），直接求解参数法。

2.1 背景值构造的改进

2.2 白化方程参数重构

背景值或灰导数的改进目的都是为了使灰微分方程与白化方程相匹配，当然也可以通过重构白化方程使其与灰微分方程相匹配，具体可通过重构白化方程的参数实现，重构依据同背景值的重构相似，即假设原始数据为离散指数序列。文献[3] 给出了重构后的白化方程及参数表达式如下：

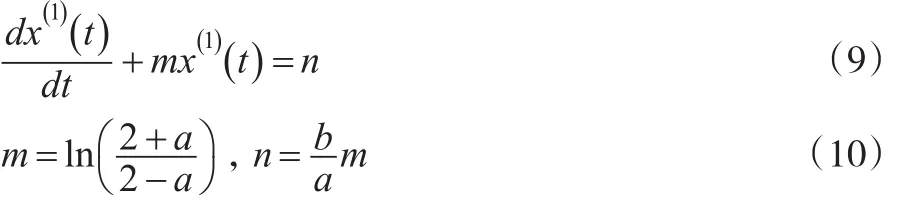
上述改进方法同样可使GM(1,1)模型满足白指数率预测无偏性，但是相对于背景值重构方法，该方法仅在原有建模步骤的基础上，增加了参数转换步骤，避免了复杂的改进算法。

2.3 灰微分方程建模

所谓灰微分方程建模即是以灰微分方程为基础建立模型，而不再考虑白化方程，从而不再存在灰微分方程与白化方程不匹配的问题。灰微分方程（3）可写为：

将上式还原即可得到拟合预测值。灰微分方程建模（离散GM(1,1)模型）同样可以满足白指数率预测无偏性。

2.4 直接求解参数法

GM(1,1)模型实际上就是一种齐次指数函数拟合方法，但是由于其存在固有缺陷而无法拟合纯指数序列，魏勇等[16]认识到了上述问题，建立了不涉及灰微分方程、白化方程概念，基于最小二乘法原理直接求解指数函数参数的方法，通过此方法建立的新模型不仅从理论上可保证是在满足给定评价标准为模拟绝对误差平方和最小、给定精度条件下的最优化模型，从而结束了灰色模型只有更优，没有最优的历史。但是，该方法需要通过编制计算机程序实现，求解难度高于其他改进方法。

式（11）成为离散GM(1,1)模型[14，15]，其递推函数形式为：

3 应用建议

总结上述GM(1,1)模型的改进方法，以直接求解参数法的拟合效果最佳，但需要借助计算机编程实现，求解难度也是最大的。背景值构造的改进方法中，数值积分方法建立的背景值与加权背景值相比，表达式更为复杂，且需要借助插值公式，求解难度较大。加权背景值表达式简单易懂，但求解最优权重需要采用迭代或搜索算法求解权重，具有一定的计算难度。离散GM(1,1)模型与传统GM(1,1)模型建模难度相当，只是离散GM(1,1)模型求解的参数是β1和β2。白化方程参数重构只是在传统GM(1,1)模型基础上增加了参数转换步骤，并未增加传统GM(1,1)模型的建模难度。

以文献[17] 提供的我国人均能源消耗量数据作为研究样本，对上述四种改进方法进行对比分析。其中，背景值改进方法以Newton-Cores公式[9]为例。由于GM(1,1)模型对初始值不具备拟合效果[4]，为了合理的对比分析，在采用直接求解参数法时，拟合数据中排除初始值。以1998—2004年的数据建模，预测2005—2007年的数据，拟合和预测结果见下页表1所示。

拟合精度的提高一直都作为评价GM(1,1)模型改进效果的依据，从最小二乘拟合原理出发，无论如何改进背景值构造都达不到直接求解参数法的拟合效果[18，19]，所以与其采用繁琐的背景值构造方法，还不如采用直接求解参数法，虽然参数求解较为复杂，却是最佳逼近结果。表2中的结果也验证了上述观点，从表2中可以看出，不论是以误差平方和还是以平均相对误差作为精度评价标准，直接求解参数法都是效果最佳的改进方法。其余三种方法均能在一定程度上提高拟合预测精度，仅背景值构造改进（Newton-Cores公式）方法并未降低拟合值的误差平方和。由于许多背景值构造改进方法建模比较复杂，本文不推荐采用此种方法。白化方程参数重构、离散GM(1,1)模型所得结果均不是最佳逼近结果，就本文实例来看，白化方程参数法重构对拟合预测精度的提高更为明显，更接近于直接求解参数法的效果。加之白化方程参数重构的建模原理简单，本文推荐采用此方法。离散GM(1,1)模型建模原理相对简单，对于近似齐次指数序列建模可以得到较好的拟合效果，实际应用中也可以考虑采用这种方法。

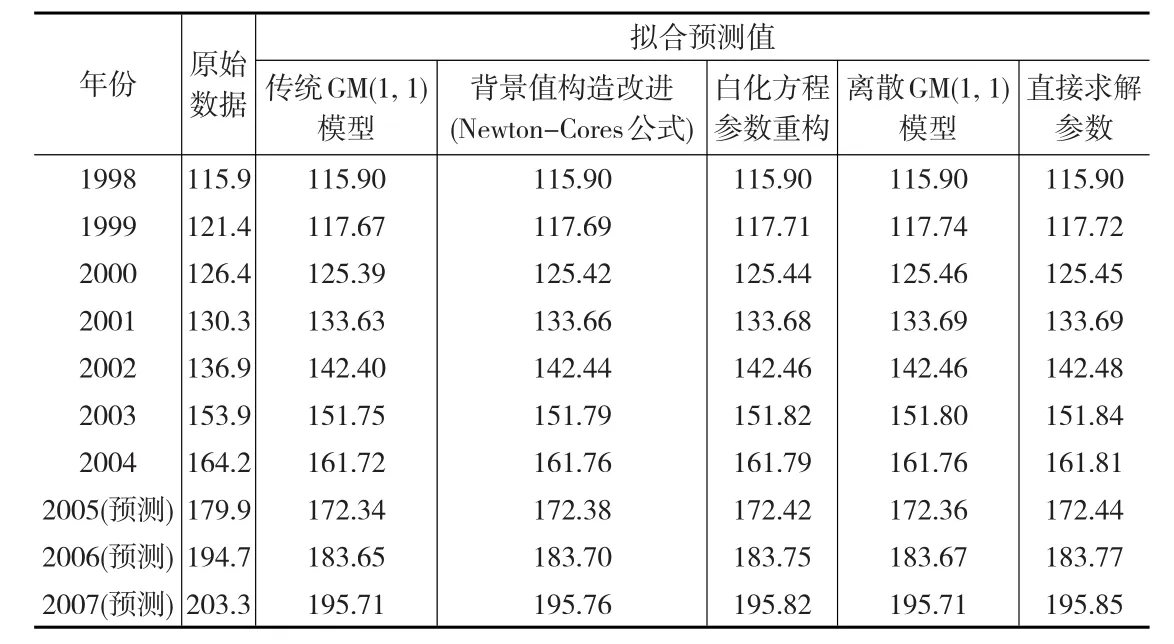
表1 我国人均能源消耗量拟合预测结果 （千克标准煤）

表2 我国人均能源消耗量拟合预测精度比较

4 结论

GM(1,1)模型是目前最常用的灰色预测模型。本文在大量已有相关研究文献的基础上从背景值构造的改进、白化方程参数重构、灰微分方程建模（离散GM(1,1)模型），直接求解参数法四个方面对当前GM(1,1)模型的改进现状进行了分析和总结。对比四种改进方法的建模难度和拟合精度，可见直接求解参数法拟合效果最优，但是建模难度最大；背景值构造改进方法大多较为复杂；白化方程参数重构、离散GM(1,1)模型建模相对简单，实例分析结果显示白化方程参数重构法与直接求解参数法拟合效果十分接近。因此，本文推荐采用白化方程参数重构法。