基于IOWA算子的多参数指数平滑模型组合预测

张贝贝，李静文，杨亚楠

（北京信息科技大学 经济管理学院，北京100192）

0 引言

事物是普遍联系的，经济系统内部各因素之间及它们同外部因素之间存在着错综复杂的交互因果关系。对经济系统的预测仅使用一种预测方法，往往导致信息不够广泛，可能会因为忽略某些因素而导致较大的预测误差，难以进行精确可靠的预测[1]。如果对同一预测问题采用各种不同的预测方法，并加以适当的组合，则能够充分地利用各种信息，达到分散预测风险、提高预测精度的目的，由此组合预测应运而生。Bates和Granger首次提出组合预测的概念[2]，即以某种加权平均的形式将各种不同的单项预测方法进行组合。组合预测模型较之单项预测模型能够更充分地反映各种预测样本信息，目前如何有效提高预测精度是预测界的热点问题，权重系数的确定和集结算子的选择一直是预测工作者研究的重点和难点。

本文构建的基于IOWA算子的组合预测模型不同于传统的组合预测模型。传统的组合预测模型中同一个单项预测方法在样本区间上各个时点的加权系数是相同的。但是对于同一个单项预测方法而言，不同时点的预测精度“时好时坏”，因而传统的组合预测方法存在一定的缺陷。本文分别使用三种多参数指数平滑模型预测出观测值在样本区间的预测值，对每个单项预测方法在样本区间上各个时点预测精度的高低按顺序赋权，并分别建立以误差平方和最小和以绝对误差绝对值之和最小为准则的新的数学规划模型，进而计算出样本区间的预测值。最后通过对比预测效果评价体系中的各个指标，表明了组合预测模型的有效性。

1 单项预测模型介绍

指数平滑模型中包含了单指数平滑模型、双指数平滑模型和多参数指数平滑模型，多参数指数平滑模型包含Holter-Winter无季节模型、Holter-Winter季节加法模型、Holter-Winter季节乘法模型[3]。鉴于多参数指数平滑模型的线性趋势及季节特性，本文使用三种多参数指数平滑模型分别对样本区间的观测值进行预测。

1.1 HW无季节模型

HW无季节模型[4]主要有两个平滑系数α、β，取值范围：（0≤α，β≤1），预测模型为：

式中：

如果t=T（最后一期），预测模型为：

其中，aT是截距，bT是斜率。

本文使用Eviews8.0软件计算原始序列的HW无季节模型预测值，计算结果如下页表1所示：

1.2 HW季节加法模型

HW季节加法模型主要有三个平滑系数α、β和γ，取值范围：（0≤α,β,γ≤1），预测模型为：

式中：

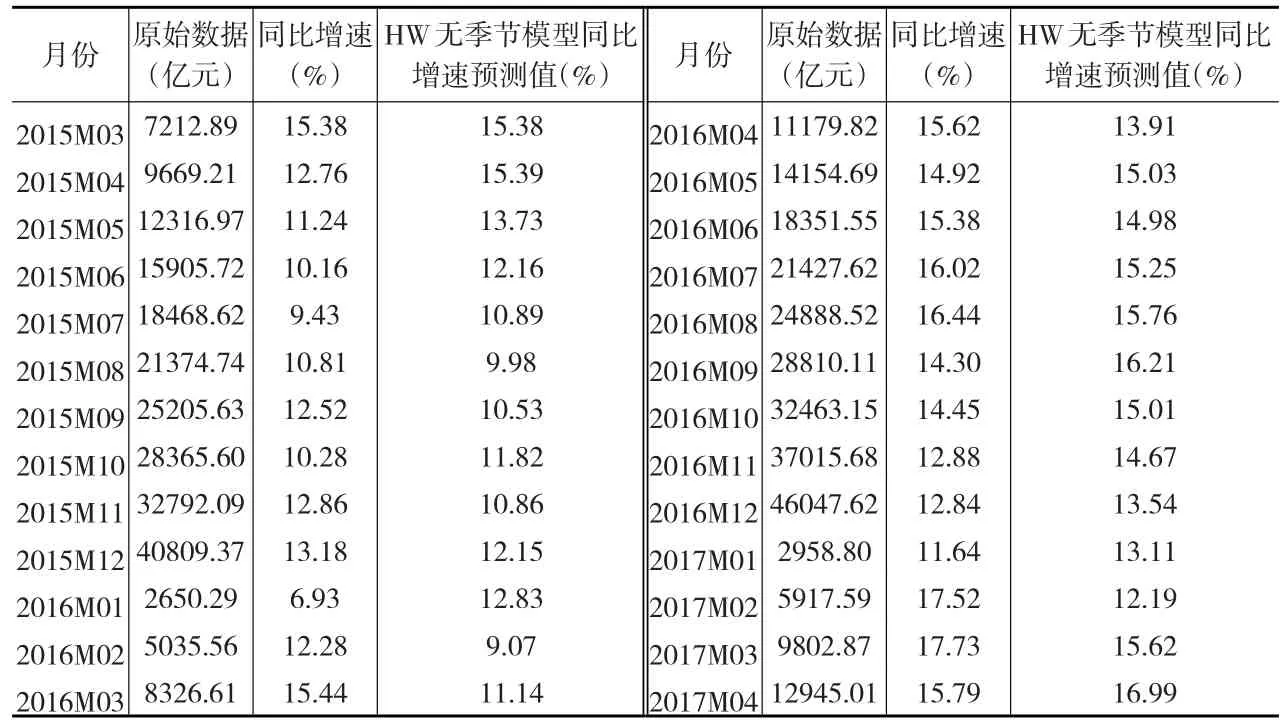
表1 HW无季节模型预测结果

其中，s是季节周期长度，月度数据，周期为12个月，即s=12；季度数据，周期为4个季度，即s=4。

如果t=T（最后一期），预测模型为：

其中，aT是截距，bT是斜率,cT是季节因子（季节指数）。可以看出他们都是通过平滑得到的。

本文使用Eviews8.0软件计算原始序列的HW季节加法模型预测值，计算结果如表2所示：

表2 HW季节加法模型预测结果

1.3 HW季节乘法模型

HW季节乘法模型[4]主要有三个平滑系数α、β和γ，取值范围：（0≤α,β,γ≤1），预测模型为：

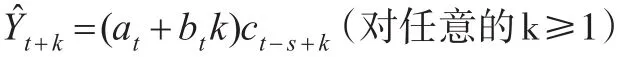
式中：

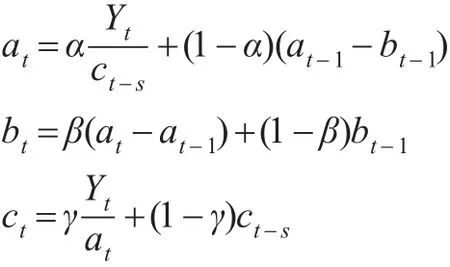
其中，s是季节周期长度，月度数据，周期为12个月，即s=12；季度数据，周期为4个季度，即s=4。

如果t=T（最后一期），预测模型为：

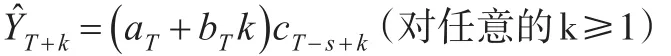
其中，aT是截距，bT是斜率,cT是季节因子（季节指数）。

本文使用Eviews8.0软件计算原始序列的HW季节乘法模型预测值，计算结果如下页表3所示：

2 基于IOWA算子的组合预测

2.1 IOWA算子的概念

定义1[5]：设OWAW：Rm→R为m元函数,T是OWAW有关的加权向量，并且满足：

式中，bi是a1，a2，a3，…，am中按从大到小的顺序排列的第i个大的数，则称函数OWAW是m维有序加权平均算子，简记为OWA算子。

例如，设w1=0.3，w2=0.4，w3=0.2，w4=0.1则由定义1可得：

实际上，OWA算子是对m个数a1，a2，a3，…，am按从大到小的顺序排序后的序列进行有序加权平均，系数wi与ai的数值无关，而仅与ai的大小顺序有关。

定 义 2[6]：设v3，a3>，…，为m个二维数组，令：

则称函数IOWAW是由v1，v2，v3，…，vm所产生的m维诱导有序加权平均算子，简记为IOWA算子，vi称为ai的诱导值，v-index(i)是v1，v2，v3，…，vm中按从大到小的顺序排列的第i个大的数的下标，W=(w1，w2，w3，…，wm)T是OWAW有关的加权向量，满足i=1，2，3，…，m。

例如，设<8,3> ，<4,7>，<2,3>，<6,1>为4个二维数组，OWA的加权向量为：W1=0.4，W2=0.25，W3=0.15，W4=0.2

则由定义2可得：

由此可知，IOWA算子是对诱导值v1，v2，v3，…，vm按从大到小的顺序排序后所对应的a1，a2，a3，…，am中的数进行有序加权平均，wi与数ai的大小和位置无关，而仅与其诱导值vi所在的位置有关。

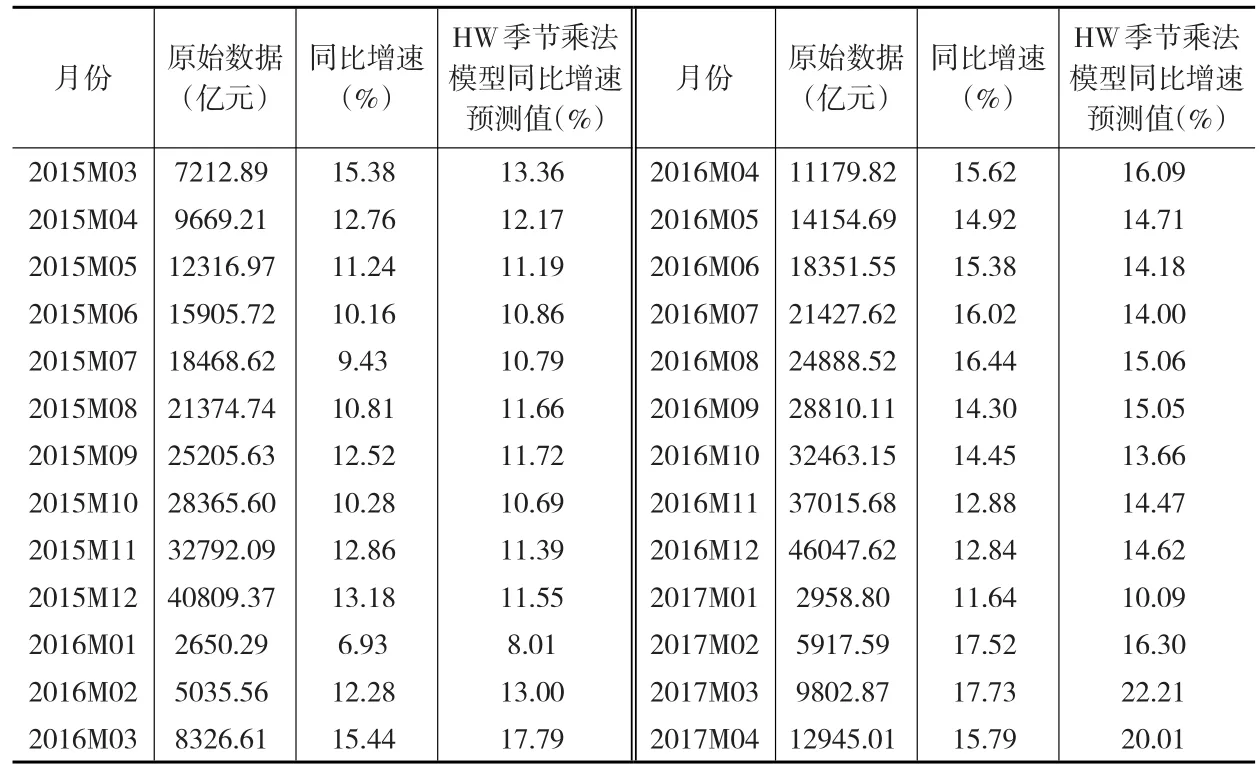
表3 HW季节乘法模型预测结果

2.2 组合预测模型建立

式中：Ait是第i种预测方法在t时刻的预测精度指标，显然Ait∈(0，1)；xt是某一序列的观测值，xit是第i种预测方法在t时刻的预测值，i=1，2，3，…，m；t=1，2，3，…，n。本文把预测精度Ait看成预测值xit的诱导值，因而第t时刻的m单项预测方法的预测精度和其对应的预测值就构成了m个二维数组：＜a1t，x1t＞，＜a2t，x2t＞，＜a3t，x3t＞，…，＜amt，xmt＞，设W=(w1，w2，w3，…，wm)T是各种预测方法在组合预测中的OWA加权向量，将m中单项预测方法在t时刻的预测精度a1t，a2t，a3t，…，amt按从大到小的顺序排列，设a-index(it)为第i个大的预测精度的下标，根据定义2有：

则式（2）称为由预测精度序列a1t，a2t，a3t，…，amt所产生的IOWA组合预测值。则n期总的组合预测误差平方和S和n期总的绝对误差绝对值之和D可表示如下：

因此，以误差平方和最小为准则的IOWA组合预测模型可表示如下：

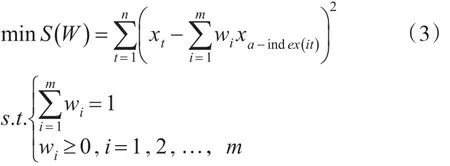
以绝对误差绝对值之和最小为准则的基于IOWA组合预测模型可表示如下：

利用非线性规划求解上述模型可以分别得出wi(i=1，2，…，m)的值，即组合预测中的OWA加权向量wi(i=1，2，…，m)使得组合预测总的误差平方和或绝对误差绝对值之和最小。

3 实证分析

本文选用中关村示范区月度累计数据进行建模预测分析，缺失数据采用比例插补法补全[7]，搜集数据时间段为2014年3月到2017年4月，实际计算中使用的是指标的同比增长率，因而数据同比增长率的长度为2015年3月到2017年4月。本文对比分析组合预测模型与各单项预测模型预测效果评价指标体系的各个指标，并预测2017年5月至2017年9月五个月的中关村高新技术园区总收入。

3.1 单项模型预测结果

根据表1至表3的预测结果，并根据式（1）计算出上述三种单项预测模型的预测精度。如表4所示：

表4 单项预测模型预测结果及其预测精度

本文三种单项预测模型均取得较好的预测效果，其中，HW季节加法模型平均预测精度>HW季节乘法模型平均预测精度>HW无季节模型平均预测精度。

3.2 IOWA组合预测

本文选取三种多参数指数平滑模型进行中关村高新技术园区总收入同比增速的组合预测。按式（2）计算IOWA组合预测值，具体计算过程如下所示：

同理：

3.2.1 误差平方和最小准则下的IOWA组合预测

将上述公式带入式（3）中，可以得出误差平方和最小准则下最优化模型：

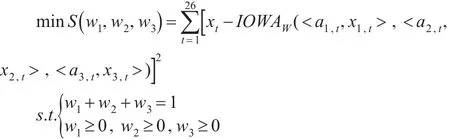
其中xt(t=1，2，…，26)是序列的原始数据同比增速值，使用EXCEL中的规划求解，或者利用MATLAB最优化工具箱，可以得出误差平方和最小准则下的IOWA组合预测模型的最优权系数为：

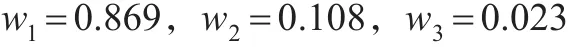
由此根据最优权系数可以计算出误差平方和最小准则下的IOWA的组合预测模型在各个时期的组合预测结果，如表5所示。

3.2.2 绝对误差绝对值之和最小准则下的IOWA组合预测

将上述公式带入式（4）中，可以得出误差平方和最小准则下最优化模型：

同理，可以得出绝对误差绝对值之和最小准则下的IOWA组合预测的最优权系数：w1=1，w2=0，w3=0

表5 误差平方和最小准则下的IOWA的组合预测结果

得出的最优权系数表明，各个时点的组合预测值为预测精度最大者所对应的单项预测值。由此根据最优权系数可以计算出绝对误差绝对值之和最小准则下的IOWA的组合预测模型在各个时期的组合预测结果，如表6所示：

表6 绝对误差绝对值之和最小准则下的IOWA的组合预测结果

3.3 模型预测对比

3.3.1 两准则下IOWA组合预测结果分析

鉴于数学期望反应数据集平均取值大小，标准差反应一个数据集的离散程度，两者结合能较好地判断模型预测结果的有效性。本文分别计算两准则下模型预测精度序列的数学期望和标准差，计算公式如下所示：

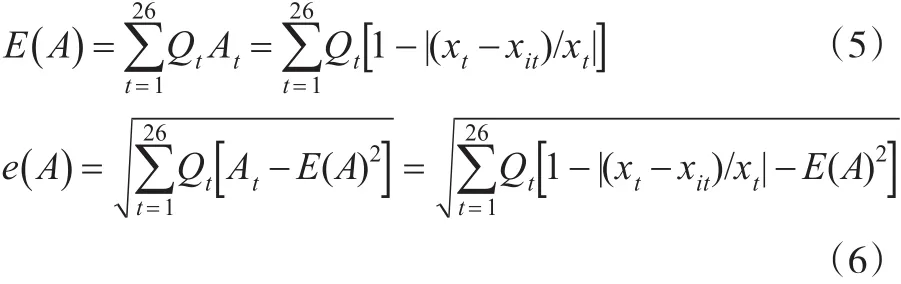
其中，E(A)为预测精度序列的数学期望；e(A)为预测精度序列的标准差；Qt为预测精度序列的离散概率分布；At为t时点预测精度。由于对预测精度序列的离散概率分布的先验信息不确知时[8]，可取因此本文中由式（5）和式（6），可以得出两准则下基于IOWA组合预测模型预测精度的数学期望和标准差，如表7所示：

表7 两准则下IOWA的组合预测精度指标

比较两准则下预测精度序列的数学期望和标准差结果可知，两者数学期望基本相同，而误差平方和最小准则下预测精度序列的标准差小于绝对误差绝对值最小准则下预测精度序列的标准差。因此，误差平方和最小准则下的IOWA组合预测模型更为有效。

3.3.2 组合预测与各单项预测结果分析

由上述分析可知，误差平方和最小准则下预测效果整体“好于”绝对误差绝对值之和最小准则下预测效果，因此本文在此基础上又具体分析了以误差平方和最小为准则建立的组合预测模型与各单项预测模型的预测结果。由表5中的组合预测数据，可以画出中关村示范区总收入同比增速和组合预测同比增速的拟合图，如图1所示，同时可以画出中关村高新技术园区总收入和IOWA组合预测总收入的拟合图，如图2所示：

图1 组合预测同比增速拟合图

由模型的计算过程可知，中关村高新技术园区总收入同比增速预测值是通过IOWA组合预测模型计算获得，从图1可以看出同比增速预测值和实际值是非常接近的。中关村高新技术园区总收入的IOWA组合预测值是通过总收入同比增速的IOWA组合预测值计算获得，从图2可以看出总收入的预测值和实际值非常接近，两者的拟合度很高。

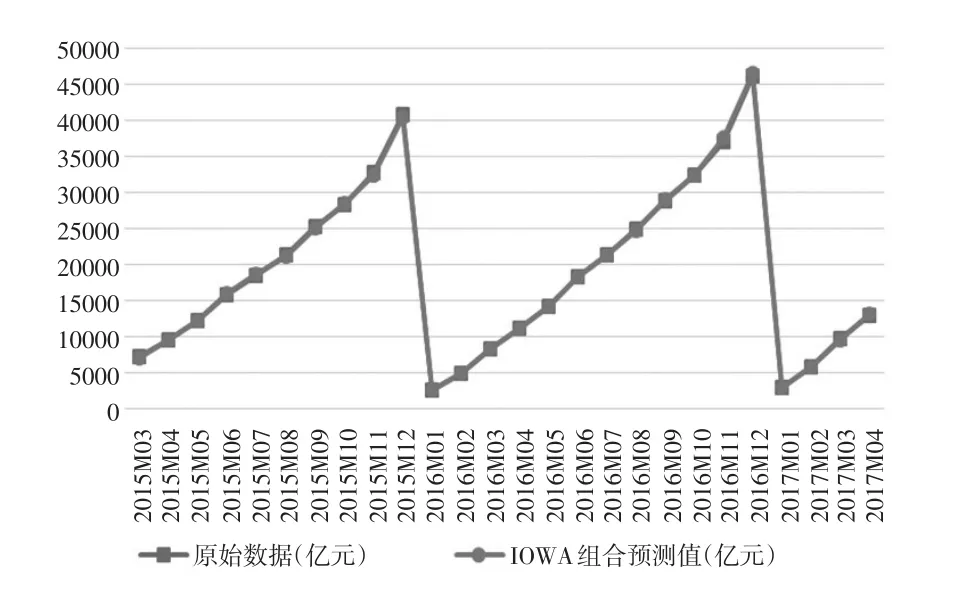
图2 组合预测总收入拟合图

为了更加明确地反映基于IOWA的组合预测模型与三种单项预测模型之间的优劣，本文计算了各模型在观测样本各个时期的平均相对误差的绝对值，具体的计算结果如表8所示：

表8 各时期的平均相对误差绝对值 （单位：%）

从表8中可以看出，基于IOWA的组合预测模型在各个时期的平均相对误差绝对值（0.70%）均小于三种单项预测模型，能有效降低预测误差，达到较好预测效果。

为了更精确地反映基于IOWA的组合预测模型与各单项预测模型的整体预测效果，本文同时选取SSE、MAE、MAPE、MSE、RMSE、MSPE等预测效果评价指标作为评价组合预测模型与各单行预测模型预测好坏的依据，其中xi为i时间的实际值，xi为i时间的预测值。

通过比较评价指标体系的各项计算值，可以明显地看出基于IOWA组合预测相对于其他三种单项预测模型的优势。计算结果如表9所示：

表9 预测效果评价指标体系

从表9计算数据来看，本文使用的基于IOWA的组合预测模型的各项误差指标值均明显低于其他三种单项预测模型的误差计算结果，从而表明本文使用的基于IOWA的组合预测模型要优于HW无季节、HW季节加法和HW季节乘法单项预测模型，从表1和表5可以得出，基于IOWA组合预测模型的平均预测精度相对于HW无季节模型、HW季节加法模型和HW季节乘法模型分别提高14.73%、7.99%和9.32%，模型的预测精度明显提高。

根据文献[9] 中提及的预测连贯性原则，可以计算样本在未来区间[n+1,n+2,……] 的预测值。计算公式如下所示：

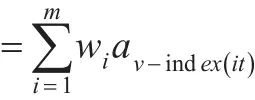
t=n+1，n+2，n+3，…；wi(i=1，2，3，…，m)为IOWA组合预测最优权系数。

IOWA组合预测值在预测区间[n+1,n+2,…] 上的诱导值，即为预测精度序列ait(i=1，2，…，m，t=n+1，n+2，…)。即若要对未来k期进行预测，则预测区间上n+k期的预测精度根据最近k期的拟合平均精度确定，即：

因而，可以得出中关村高新技术园区2017年5月至2017年9月的预测值，如表10所示：

表10 未来5期预测值