采用完整性威胁树的信息流完整性度量方法1

吴奇烜，马建峰，孙聪



采用完整性威胁树的信息流完整性度量方法1

吴奇烜1,2，马建峰1，孙聪1

（1. 西安电子科技大学网络与信息安全学院，陕西 西安 710071；2. 腾讯科技(深圳)有限公司，广东 深圳 518057）

针对传统信息流完整性分析方法缺乏对具体系统结构及关联性攻击事件考虑的缺陷，提出完整性威胁树对系统信息流完整性做量化分析，提出条件触发门对存在关联的攻击事件进行建模。使用攻击代价来量化攻击各信道的难易度，依据架构相关的完整性威胁树，利用可满足性模理论及其工具求解最小攻击代价，以量化分析系统完整性威胁。通过对实际飞控系统模型的建模分析求解说明方法的实用性，并得出条件触发门参数对系统完整性的影响。

完整性；信息流；可满足性模理论；攻击树

1 引言

计算机系统的安全性要求包括机密性、完整性和有效性等方面。在安全关键的嵌入式控制系统中，嵌入式程序、控制指令和系统配置均具有高完整性要求。信息流完整性是指基于细粒度策略保证与系统架构相关的低完整性信息的流动对高完整性数据（指令、配置）的干扰符合特定的策略规则。现有的定性信息流完整性模型存在诸多不足。Denning[1]提出的信息流安全格模型通过分析数据在系统中的流向来验证信息在不同实体间传递的安全性。以BIBA模型[2]为主流的严格信息流完整性模型，依据完整性等级划分对信息的流向进行控制，确保低等级数据不能流向高等级数据。这些用于防止信息非授权修改的定性模型有时太过严格，导致系统效率及应用兼容性等问题[3]。

实际上，程序在运行过程中往往需要使用一些低完整性的数据（如网络数据），这本身会破坏严格的信息流完整性策略。大量场景仅要求威胁程度在可容许的范围内，而无须保证系统绝对安全，因此对于完整性的定量分析必不可少。针对格模型只能定性分析系统安全性的不足，Millen[4]基于信息论中信息熵提出了无干扰与互信息的关系，首次设计了量化信息流安全模型，但其度量结果不够准确。此后，Clarkson等[5]以互信息为基础，提出了量化信息流的污染与抑制，给出了完整性破坏度的计算方法。上述的量化信息流完整性模型仅适用于抽象的系统模型，难以对结构复杂的实际系统进行威胁分析。

攻击树因其简洁直观的描述方式而广泛应用于解决“攻击−防御”场景下的量化安全分析评估[6]。针对系统可能受到的攻击，攻击树能够进行与具体系统结构相关的量化安全性建模，其局限性在于以下两方面。一方面，由于传统攻击树仅包含“与门”和“或门”，无法对实际攻击中的复杂攻击事件关系进行建模，因而表达能力有待扩展。Jhawar等[7]针对序列化攻击使用SAND门扩展了攻击树的动态建模能力，但模型无法描述存在条件关联的攻击事件。另一方面，虽然近期研究引入形式化手段提升攻击树的建模准确性[8]及面向特定属性的推理能力[9]，但其求解方法仍主要由各叶节点基本攻击事件的成功概率分析预测根节点攻击目标的成功概率，不适用于对系统完整性进行量化分析，需要更细粒度的节点完整性定义。

本文将量化信息流完整性模型与攻击树的系统架构相关建模能力相结合，研究复杂组件化系统的信息流完整性威胁分析方法；提出完整性威胁树并定义了对应的量化信息流完整性模型；针对当前攻击树描述能力的不足，提出条件触发门用以描述存在条件关联的攻击事件；利用可满足性模理论（SMT，satisfiability modulo theories）对完整性威胁树进行求解，得出针对目标系统的最小攻击代价和相应的攻击方式；针对实际飞控系统模型的分析和求解说明方法的实用性。

2 信息流完整性的量化定义

本文基于信息论概念定义信道（channel）的完整性模型。在实际环境中，用户和攻击者均能向信道提供输入并从信道获取输出。攻击者通过提供不可信的输入破坏信道的数据完整性。

理想情况下，信道规约（specification）接收可信输入in并产生可信输出spec，如图1(a)所示。而在威胁场景下（一般对于具体信道实现而言），由于存在攻击者，信道不仅从用户接收可信输入，还从攻击者接收不可信输入in，此时信道输出的完整性遭到一定程度破坏，产生被污染的输出impl，如图1(b)所示。通过观察对比impl和spec，即可得到真实输出的完整性受影响的程度，这一程度反映出可信输出受不可信输入影响而丢失的信息量。定义信息流抑制（suppression）表示此信息量，作为信息流完整性的量化定义。

定义1 信息流抑制指用户无法从impl获得关于spec的信息量，即由于攻击者不可信输入而使真实输出丢失的信息量。信息流抑制的计算公式为

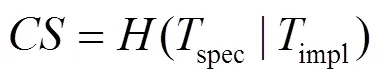
其中，Tspec为tspec的概率分布，Timpl为timpl的概率分布，H(Tspec|Timpl)指用户在已知Timpl的前提下得到Tspec的熵。

3 基于完整性威胁树的信息流完整性建模

针对具体系统的信息流完整性攻击，定义为由攻击者实施的一系列输入操作，这些操作使系统正常的数据交互出现错误，如产生数据丢失等。复杂的信息流完整性攻击，即针对影响目标系统信息流完整性的一组信道，按照一定步骤实施不可信输入的过程。

信息流完整性攻击的难易程度可由捕获信道知识所需付出的代价（cost）进行量化。系统中某信道的cost定义如下。

cost()=(in,spec)×

其中，为令=(spec)时，in的比特数。(in,spec)为信道的in与spec间的互信息(mutual information)，表示在没有攻击者干扰的前提下信道所传输的数据量，其中，in为in的概率分布。

因此，给定信道集合={1,…,c}，攻击代价cost()定义为

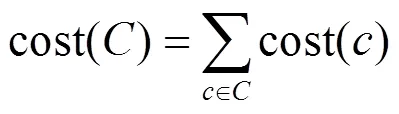
本文将针对目标系统的信息流完整性攻击表示为树形结构，称为完整性威胁树。完整性威胁树的根节点表示攻击所要达成的最终目标，叶节点表示实现这一攻击效果可能采取的手段（即在各信道上实施非可信输入），各中间节点表示要达成最终攻击效果所经历的子目标。每个节点以其各子树的cost值为输入，并输出一个cost值，所输出的cost值表示实施该子目标节点对应攻击所需付出的代价。参考攻击树定义[6]，完整性威胁树的连接门包括与（AND）门和或（OR）门，AND门表示达成其完整性攻击目标要求其子树对应攻击目标全部完成，其输出为所有子节点的代价之和；OR门表示达成其完整性攻击目标要求其任一子树对应攻击目标完成，其输出为所有子节点中代价最小的节点的代价。

在实际系统中，存在一系列相互关联的信息流完整性攻击事件，无法使用AND或OR门进行建模分析。例如，在飞控计算机系统中，表决模块需要在表决前后分别读写表决存储器以完成表决，该存储器的完整性被攻击者破坏后，对表决模块的攻击难度相比直接攻击该模块而言大大降低。针对此类关联性攻击事件，本文提出条件触发门对其进行建模分析。

定义2 条件触发门是一种接收若干主输入与若干触发事件，且产生单一输出事件的门结构。当主事件全部发生时输出事件发生，而触发事件将导致主事件的cost变为正常状态下的倍（0≤≤1），其图形表示如图2所示。

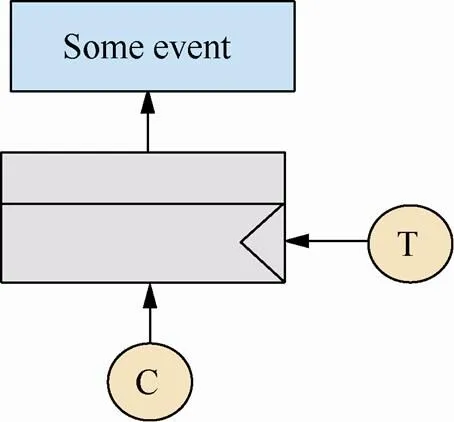
图2 条件触发门的图形表示

条件触发门的使用条件即系统某些信道之间存在依赖关系，当其中一个信道遭到攻击后，对其他信道的攻击难度产生一定影响。在图2中，成功攻击信道C将达成相关攻击目标，此时Some event的代价等于攻击信道C的代价；信道T与该目标无直接联系，但攻击T将导致C的攻击代价降低，从而降低攻击目标的总代价，则Some event的代价等于攻击T的代价加C的代价的倍。

一旦攻击过程确定，即可以将系统中各个信道上的攻击代价作为叶节点，建立对应的完整性威胁树模型，从而明确得出需要攻击哪些信道及如何组合才能达到攻击目标。具体建立步骤如下。

1) 分析被评估系统，确定攻击最终目标，以该目标作为完整性威胁树的根节点，即顶层事件。

2) 从根节点开始，分析达成该目标所需要达成的子目标，根据这些子目标之间的逻辑关系，通过基本门结构及定义的条件触发门将其连接到总目标节点下方，构成树的下一层节点。

3)对每一个子节点，重复第2)步的过程，采取自上而下的方法逐步递推，直到其子目标无法继续分解且已是对某个具体信道的攻击事件为止。

4) 对树的每一个叶节点，计算其所攻击的信道需付出的代价，作为其攻击代价写入节点。

4 信息流完整性的最优化求解

利用完整性威胁树对系统攻击过程进行建模，可根据攻击系统各信道所需的代价（叶节点）计算出攻击系统所需的代价（根节点）。为了计算出攻击系统所需的最小代价，需要求解受布尔条件约束的最优化问题。本文提出基于SMT的最优化求解方法，用于分析攻击系统所需的最小代价，即根据各信道的cost，找到一个信道集合goal，使该集合中所有信道的cost能够保证攻击系统所需代价最小。

该最优化问题可通过计算一系列SMT问题模型Π={Π1,…,Π}求解。每个Π由两方面约束组成：1)所选goal使顶事件发生；2)由goal中信道求得的顶事件目标值goal比当前goal值小。初始条件Π1下，goal值为+∞。若该树存在某信道集合，使攻击者通过捕获这些信道达成攻击目标，则goal值必小于+∞；而若最终求得goal值为+∞，则说明根据该完整性威胁树分析的系统是安全的，攻击者无法触发顶事件。迭代过程由Π得到Π+1，Π+1的约束强于Π，从而得到对于攻击目标的一个更小的代价。当Π+1不可满足时算法停止，当前模型中包含的信道代价之和即为实现攻击目标的最小代价。目标函数定义为如下形式。

式中为所有叶节点个数，即系统中总信道数，S为布尔类型，代表该信道是否被选入攻击模型。当前模型可满足时，添加新的约束以减小goal值，直到模型不可满足为止。本文基于SMT求解器设计算法1，用于求解最优化cost。其中，={1,…,S| 1≤≤,S=0/S=1}保存使第一方面约束可满足的信道选择约束，SMT求解器能够通过check检验中的约束是否满足并返回SAT（可满足）或UNSAT（不可满足）。判断模型是否SAT是一个NP完全问题，已有多种成熟的理论及工具支持其求解。

算法1 基于SMT的最优代价求解算法

输入 P(VT)：由完整性威胁树转化得到的约束集；cost()：叶节点cost

输出：攻击目标系统的最小cost

开始

1) Init SMT solver : S ← Ø ;

2) Minimal cost :← ∞ ;

3) S.add(P(VT));

4) for∈V0do /*初始化节点参数*/

5) S.add(cost()); /*仅基本组件*/

6) S.add(P(= 0) + P(= 1) = 1);

7) while S.check(Π) == SAT do

8) M ← S.model ;

9)← goal(M);

10) Π ← M ∧()

11) Return

End

初始问题模型（model）Π1下，goal值为+∞。若该树存在某信道集合，使攻击者通过捕获这些信道达成攻击目标，则goal值必小于+∞；而若最终求得goal值为+∞，则说明根据该完整性威胁树分析的系统是安全的，攻击者无法触发顶事件。迭代过程的每一步由Π得到Π+1，Π+1的约束强于Π，goal值更小，从而得到对于攻击目标的一个更小的代价。当Π+1不可满足时算法停止，当前模型中包含的信道代价之和即为实现攻击目标的最小代价。

5 实例研究

本节针对双余度飞行控制系统实例，说明本文信息流完整性威胁建模及最优化求解方法的实用性。由于攻击者能够通过在飞控系统信道注入信号、从物理侧或网络侧注入组件故障等方式展开系统信息流完整性攻击，且攻击可通过系统组件交互和条件依赖关系传播，因而针对系统进行信息流完整性威胁建模和最小攻击代价评估，是找出关键完整性威胁并进行加固的基础。

飞机飞控系统由双余度计算机（CS1/CS2）和交叉控制器（IC, interactive controller）组成[10]，如图3所示。双余度计算机同时使用数据总线接收当前数据，然后分别根据接收的数据同步执行相同的计算过程，表决计算结果，实现对飞行姿态或方位、飞行轨迹、结构模态等的操纵控制。交叉控制器负责计算过程中数据的交叉传输（IT, interactive transmission）并执行所有的容错服务，包括故障检测（FD, fault detection）、故障类型判断（FTD, fault type determination）、故障定位（FL, fault localization），并在永久性故障后重新配置系统。

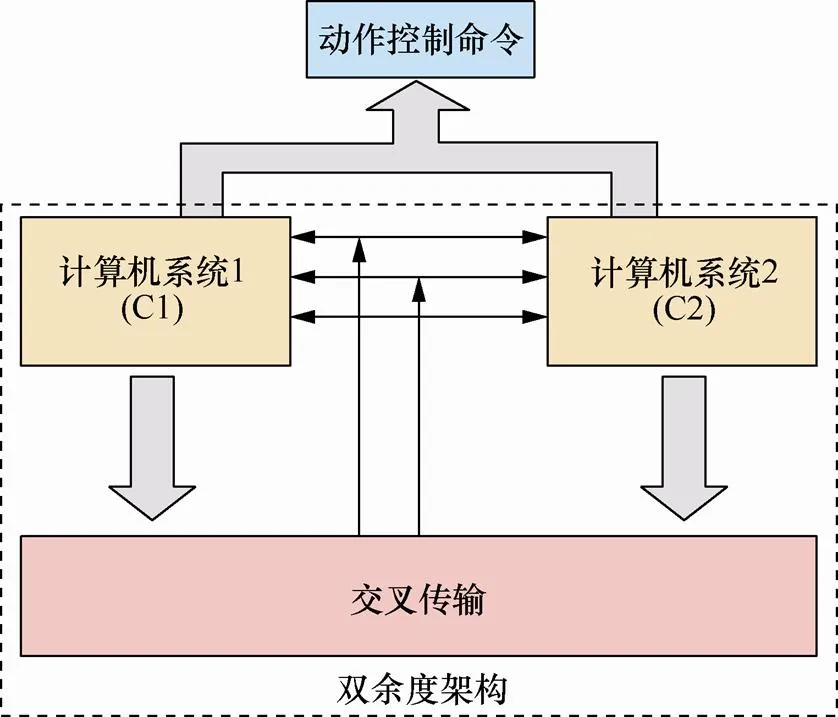
图3 飞控系统双余度架构

其中，单个计算机节点主要由数据采集模块、表决模块和控制率计算模块构成。数据采集模块（DC，data collecter）收集外围设备的数据（如传感器采集的飞行状态等），对传感器数据使用Kalman滤波进行降噪。表决模块由用于记录上次表决结果的表决存储器（VM，vote memory）和表决控制器（VC，vote controller）组成，负责对双通道数据进行表决。控制率计算模块（CLC，control law compute）使用输入表决的数据作为输入，调用控制率算法计算出飞机飞行模态等数据。

针对该飞控系统建模得到的完整性威胁树如图4所示。使系统瘫痪的攻击有两种情况：一是攻击CS1和CS2使其同时发生故障，此时由于双余度均无法得到正确的控制信号，飞控系统无法正确运行；二是攻击CS1或CS2中任一计算机，同时攻击交叉传输模块，使冗余容错机制瘫痪，虽然另一计算机仍在正常工作，但由于交叉传输模块的故障CS1与CS2无法正确交互，也会导致整个系统瘫痪。为了说明本文提出的完整性度量方法的实用性，本文分别针对采用两种不同控制率算法[11-12]的双余度飞控计算机系统进行完整性威胁分析。依据飞机在大地坐标系的横侧向动力学模型[12-13]，结合实际飞控系统[11]，估算两系统中各模块接收输入数据量、输出数据量，如文献[12]中控制律输出结果为方向舵偏角及副翼偏角，约16.98 bit，输入包括舰载机质量、速度侧向分量、滚转角、滚转角速率、偏航角速率、俯仰角等，约35.64 bit，其余模块按照类似方法计算可得表1的第2、4列。再根据本文前述cost定义求得攻击各模块的代价，如表1所示。

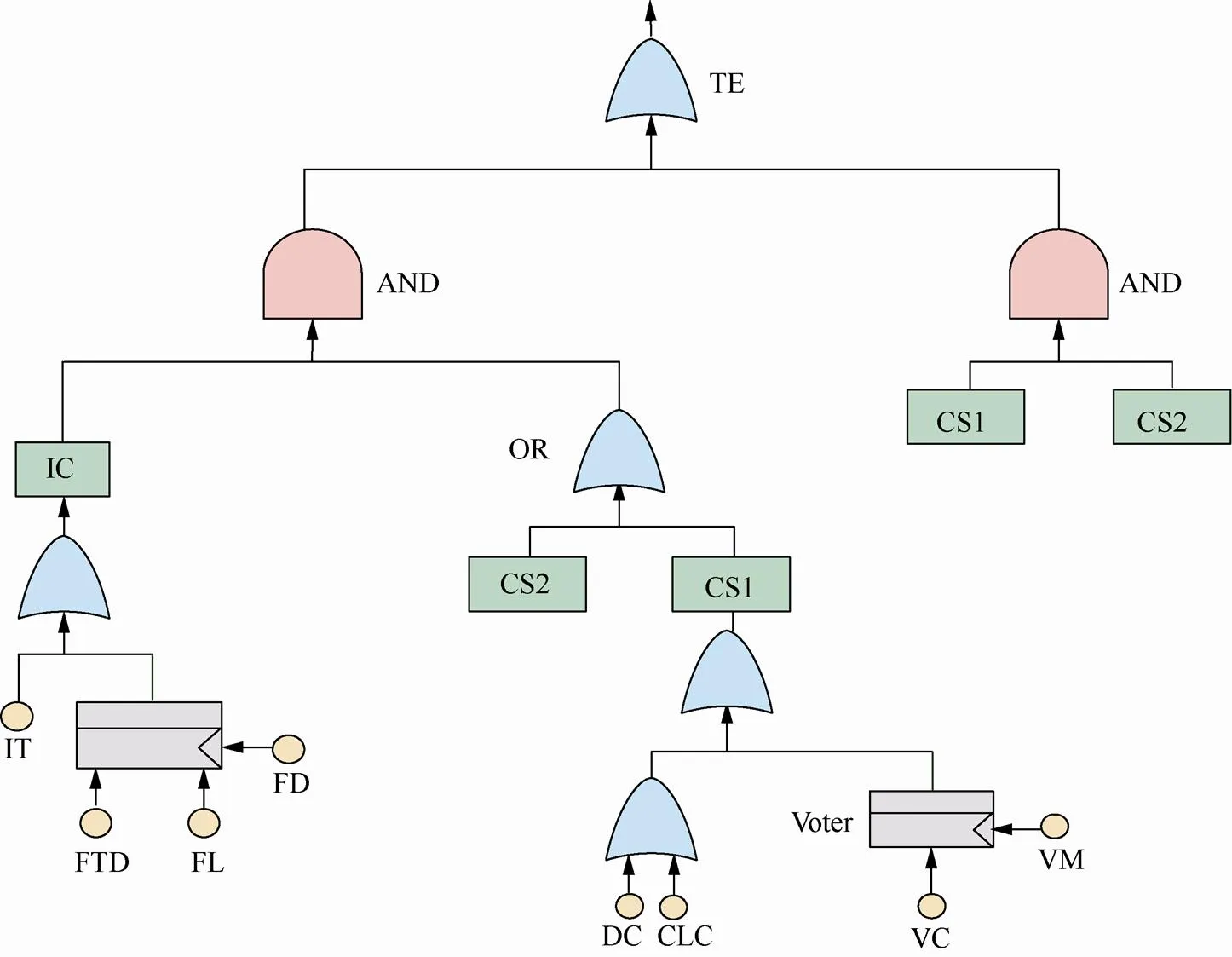
图4 飞控系统完整性威胁树示意

表1 控制律与模块cost对照

使用Python基于SMT求解器z3实现算法1，以表1数据作为叶节点参数对图4所示完整性威胁树进行攻击代价最优化求解。实验结果如图5所示。

图5 条件触发门与系统cost的关系

图5(a)显示攻击者成功破坏系统所需最小cost（TEC，top event cost）随条件触发门参数（∈[0,1]）的变化。在较小时，先破坏表决存储器使表决模块被攻破能取得较大收益，从而TEC随呈线性增长，而当大于0.7、0.8后（分别对应两种控制律），破坏表决存储器的收益过低，从而直接攻击表决控制器反而能节省攻击代价，全局攻击代价变得与变化无关，故曲线呈水平。图5(b)表示当设为0.3时，攻击者成功破坏系统所需最小cost随表决存储器的cost值的变化，表决存储器cost取值范围为[100，300]。在表决存储器的cost较小时，其作为条件触发门的触发事件影响着攻击整个系统所需的cost，但在触发事件cost增大到一定程度后，直接攻击表决控制器反而能节省攻击代价，因而曲线呈水平。

图5(a)和图5(b)反映出条件触发门能够正确建模相互关联的攻击事件。图5(c)在降低Quad-Sim控制律计算模块cost的情况下，观察攻击者成功破坏系统（及其模块）所需最小cost随条件触发门参数的变化。图5(c)中，CLC模块的cost由于不受影响，因而为一条水平线，Voter模块的cost则随着的增大而呈与图5(a)类似趋势，飞控计算机（CS）的cost取值始终与两者中较小的一方保持一致，且TE模块cost变为水平线的转折点（与CS相同）。证明了本文提出的基于SMT的最优化求解方法能够正确分析得出攻击系统所需的最小代价。

6 结束语

为了满足当前计算机系统完整性的需求，针对当前信息流完整性量化模型的不足，本文将量化信息流完整性模型与攻击树的系统架构相关建模能力相结合，提出了完整性威胁树并给出了完整性量化模型。在此基础上，本文实现了一种基于SMT的最优化求解方法，用于分析攻击系统所需的最小代价，以进一步分析系统威胁。最后，本文结合飞控双余度计算机系统做了完整性分析，说明方法的实用性。

[1] DENNING D E. A lattice model of secure information flow[J]. Communications of the ACM, 1976, 19(5):236-243.

[2] BIBA K J. Integrity considerations for secure computer systems: technical report: ESD-TR-76-372[R]. 1977.

[3] 吴泽智, 陈性元, 杨智, 等. 信息流控制研究进展[J]. 软件学报, 2017, 28(1): 135-159.

WU Z Z, CHEN X Y, YANG Z, et al. Survey on information flow control[J]. Journal of Software, 2017, 28(1): 135-159.

[4] MILLEN J K. Covert channel capacity[C]//IEEE Symposium on Security and Privacy. 1987: 60.

[5] CLARKSON M R, SCHNEIDER F B. Quantification of integrity[J]. Mathematical Structures in Computer Science, 2015, 25(2): 28-43.

[6] KORDY B, PIETRE-CAMBACEDES L, SCHWEITZER P. DAG-based attack and defense modeling: don’t miss the forest for the attack trees[J]. Computer Science Review, 2014, (13-14): 1-38.

[7] JHAWAR R, KORDY B, MAUW S, et al. Attack trees with sequential conjunction[C]//The 30th IFIP TC 11 International Conference, 2015:339-353.

[8] AUDINOT M, PINCHINAT S, KORDY B. Is my attack tree correct [C]//The 22nd European Symposium on Research in Computer Security. 2017: 83-102.

[9] HOME R, MAUW S, TIU A. Semantics for specialising attack trees based on linear logic[J]. Fundamenta Informaticae, 2017, 153(1-2): 57-86.

[10] SAMET R. Recovery device for real-time dual-redundant computer systems[J]. IEEE Transactions on Dependable and Secure Computing, 2010, 8(3):391-403.

[11] MAHONY R. KUMAR V. CORKE P. Multirotor aerial vehicles: modeling, estimation, and control of a quadrotor[J]. IEEE Robotics and Automation Magazine,2012,19(3):20-32.

[12] 张杨, 吴文海, 汪杰. 舰载无人机横侧向着舰控制律设计[J]. 航空学报, 2017, 38(S1):128-134.

ZHANG Y, WU W H, WANG J. Design of carrier UAV lateral/di rectional landing control law[J]. Acta Aeronautica ET Astronautica Sinica, 2017, 38(S1):128-134.

[13] HARTLEY E N, MACIEJOWSKI J M. A longitudinal flight control law based on robust MPC and H2 methods to accommodate sensor loss in the reconfigure Benchmark[J]. IFAC Papers Online, 2015, 48(21):1000-1005.

Information flow integrity measurement method using integrity threat tree

WU Qixuan1,2, MA Jianfeng1, SUN Cong1

1. School of Cyber Engineering, Xidian University, Xi’an 710071,China 2. Tencent Technology (Shenzhen) Company Limited, Shenzhen 518057, China

In order to avert the drawback of traditional information flow integrity analysis on ignoring the specific system architecture and associated attack events, an integrity threat tree to quantify the integrity of the system information flow, and the conditional trigger gate to model the associated attack events were proposed. The attack cost was used to quantify the degree of difficulty on attacking each channel. According to the architecture-related integrity threat tree, the minimum attack cost and corresponding target channel set required to achieve the attack target were solved by using the satisfiability modulo theories. The practicality of our approach was demonstrated by the modeling and analysis of the actual flight control system models, and the influence of the conditional trigger gate parameters on the system integrity was discussed.

integrity, information flow, satisfiability modulo theories, attack tree

The National Science Foundation of China (No.61872279)

TP309

A

10.11959/j.issn.2096-109x.2019016

吴奇烜（1992− ），男，陕西商洛人，西安电子科技大学硕士生，主要研究方向为系统可靠性分析、信息流安全。

马建峰（1963− ），男，陕西西安人，博士，西安电子科技大学教授、博士生导师，主要研究方向为密码学、网络安全。

孙聪（1982− ），男，陕西兴平人，博士，西安电子科技大学副教授、博士生导师，主要研究方向为信息流安全、可信软件。

2018−10−10；

2019−01−20

孙聪，suncong@xidian.edu.cn

国家自然科学基金资助项目（No.61872279）

吴奇烜, 马建峰, 孙聪. 采用完整性威胁树的信息流完整性度量方法[J]. 网络与信息安全学报, 2019, 5(2): 50-57.

WU Q X, MA J F, SUN C. Information flow integrity measurement method using integrity threat tree[J]. Chinese Journal of Network and Information Security, 2019, 5(2): 50-57.