外部与内部激励对正时齿轮传动系统动力学的影响*

兴艳

(1.中北大学机械工程学院 山西太原 030051；2.兵器工业第七〇研究所 天津 300400)

发动机正时传动系统可以将曲轴产生的动力传递给配气机构及其他工作系统，从而保证配气机构及各工作系统的准确运转。正时传动系统包括齿轮传动、链条传动、皮带传动3种形式，其中齿轮传动具有结构相对紧凑、传递效率高、工作过程可靠、使用寿命长的特点，是柴油机正时传动系统最常用的形式[1]。

当前柴油机正时齿轮传动系统主要存在两大难题：齿轮的疲劳强度与振动噪声。齿轮的振动与冲击属于齿轮动力学范畴，因此从动力学的角度研究齿轮产生振动与冲击的原因，可为齿轮传动系统的优化改进提供相关的指引。邓晓龙和刘国庆[2]使用EXCITE TD软件建立了变速箱齿轮系统的动力学模型，研究了曲轴转速波动对变速箱齿轮转速、角加速度、转矩的影响。郭磊等人[3]在动力学模型基础上，分析了啮合时变刚度、自由惯量、齿侧间隙对动力学特性的影响。薛爽等人[4]建立了正时齿轮系统多体动力学模型，分析了不同转速下转速波动对啮合冲击造成的影响，更深一步地分析了曲轴加装扭转减振器后不同转速下冲击力的变化。李一民[5]建立了正时齿轮系统多体动力学模型，分析了考虑齿轮负载及曲轴角速度下的齿轮扭转角位移、啮合齿相对运动以及动态啮合力。

以上研究均是单一地针对外部或内部激励进行分析，未同时考虑外部与内部激励对齿轮传动特性的影响。本文作者在齿轮传动动力学原理的基础上，建立了柴油机自由端正时齿轮传动系统的动力学模型，分别研究了外部与内部激励对正时齿轮传动特性的影响，为正时齿轮传动系统的设计提供了参考。

1 动力学模型的建立

1.1 齿轮啮合动力学原理

齿轮副动力学模型为

Rgθg-e(t))=Tp(t)

(1)

Rgθg-e(t))=-Tp(t)

(2)

式中：Ip、θp、Rp分别表示驱动轮转动惯量、驱动轮扭转角位移、驱动轮基圆半径；Ig、θg、Rg分别表示从动轮转动惯量、从动轮扭转角位移、从动轮基圆半径；Cm、K(t)、e(t)、Tp(t)分别表示齿轮啮合阻尼、时变啮合刚度、静态传递误差、外部扭矩[6-8]。

正时齿轮传动系统动力学的动态激励分为系统外部激励与系统内部激励。系统外部激励是指驱动轮的输入扭矩和从动轮的负载扭矩，系统内部激励包括时变啮合刚度激励、误差激励以及齿轮间隙引起的冲击激励[9]。

1.2 参数设置

出于研究方便的考虑，建立的模型只包括曲轴齿轮、复合惰轮(大、小惰轮)、凸轮轴齿轮以及相应的止推轴承与径向轴承，齿轮系布置图如图1所示。模型的所有齿轮均为斜齿轮，模数为2.75，压力角为20°，螺旋角为-10°，表1给出了相关齿轮参数。

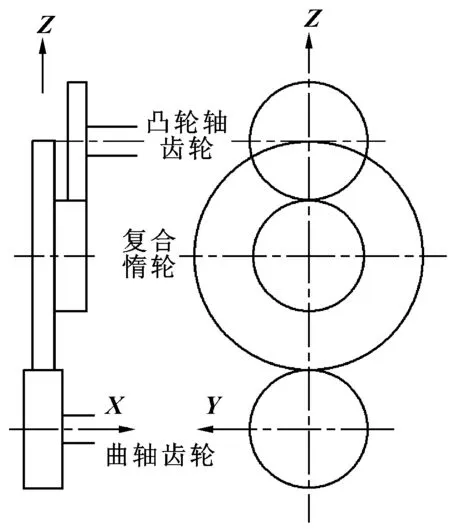
图1 齿轮系布置图

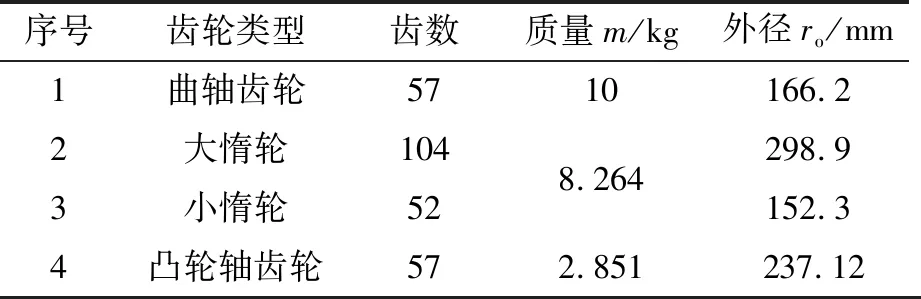
序号齿轮类型齿数质量m/kg外径ro/mm1曲轴齿轮5710166.22大惰轮1043小惰轮528.264298.9152.34凸轮轴齿轮572.851237.12

1.3 动力学模型

在EXCITE TD软件中建立正时齿轮传动系统动力学模型，模型中齿轮简化为独立质量单元，包含了齿轮的质量与转动惯量等参数，模型如图2所示。模型中的动力通过齿轮间的坐标与啮合点的位置进行传递，齿轮模型之间力的传递考虑了齿轮的啮合刚度与啮合阻尼的影响。

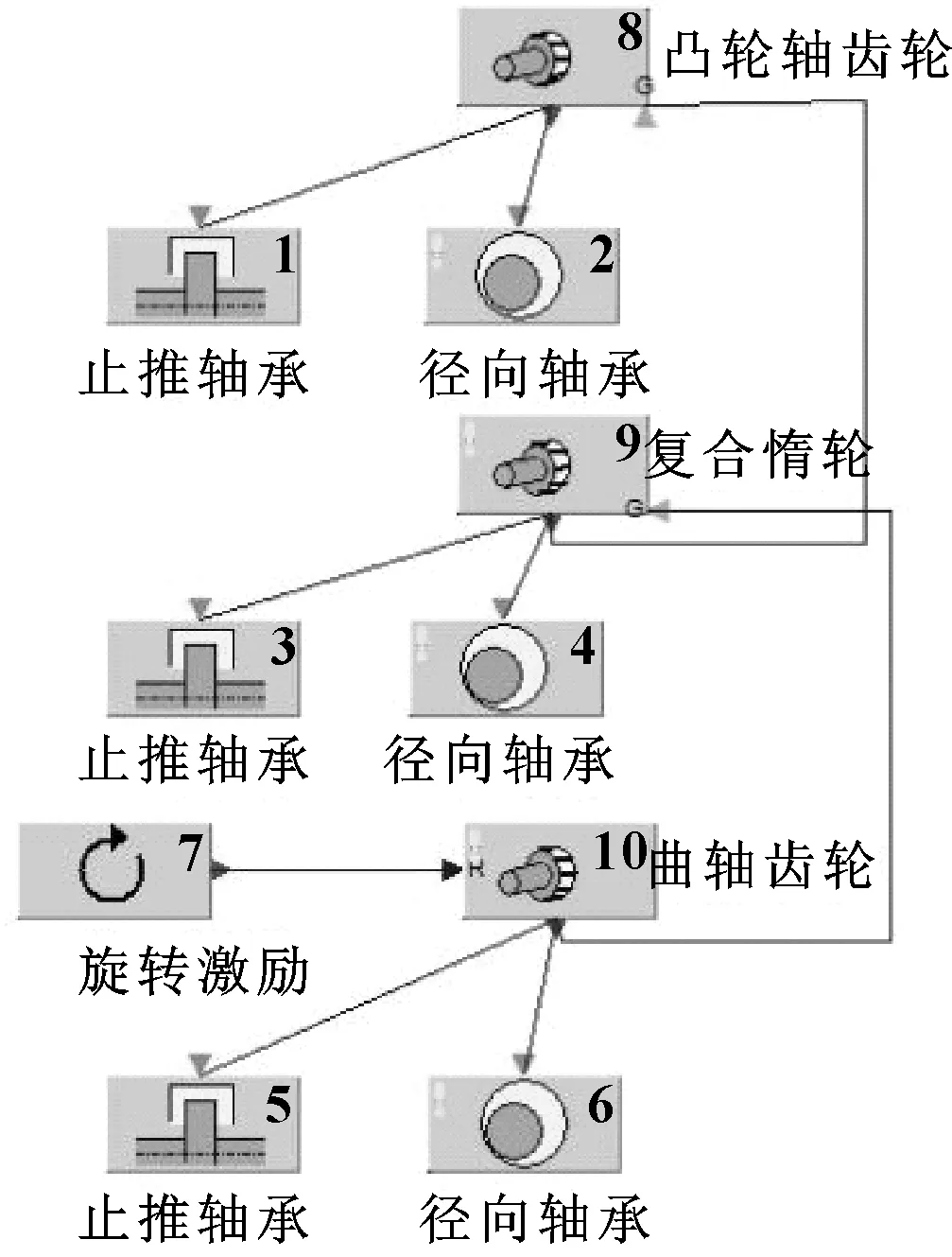
图2 齿轮传动系统的动力学模型

1.4 曲轴转速波动与凸轮轴齿轮负载

在AVL_EXCITE Designer 中建立曲轴动力学模型，在结果中获取曲轴自由端转速波动曲线如图3所示。在TD中建立配气机构全阀系动力学模型，通过设置不同转速获取凸轮轴齿轮的2个负载扭矩如图4所示，其中负载1的最大扭矩绝对值为566 N·m，负载2的最大扭矩绝对值为912 N·m。

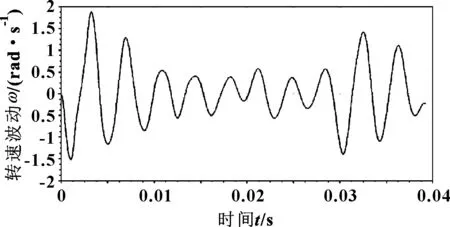
图3 3 000 r/min时曲轴转速波动

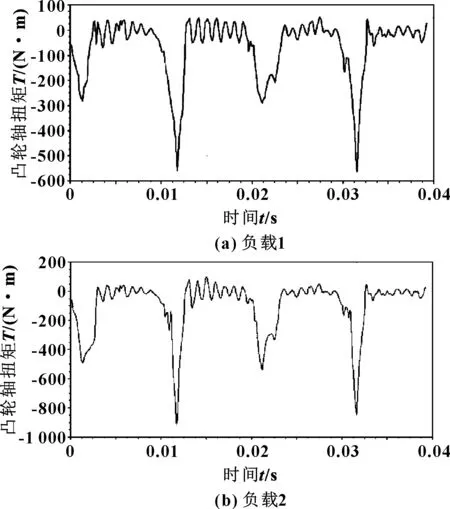
图4 凸轮轴齿轮负载扭矩

2 外部激励对正时齿轮传动系统动力学影响

曲轴转速波动与齿轮负载扭矩作为齿轮传动系统的重要的激励源，对齿轮传动系统的动力学特性有着显著的影响，所以研究曲轴转速波动与齿轮负载扭矩对齿轮传动系的影响也就至关重要[10]。

2.1 凸轮轴齿轮负载扭矩对动力学影响

图5所示为凸轮轴齿轮角速度变化曲线，图6与图7所示为凸轮轴齿轮与复合惰轮啮合力变化曲线。可以看出：随着负载的增大，角速度与啮合力峰值均有较大的增大，且角速度波动明显增加；角速度峰值绝对值由5.26 rad/s增大到6.95 rad/s，啮合力峰值绝对值由负载1时的9 581.79 N增大到了负载2时的17 370.4 N，增大了7 788.61 N。对比图4所示负载曲线，可以看出角速度与啮合力曲线峰值位置与负载峰值位置相近，说明角速度与啮合力峰值受负载影响较大；此外，由于存在负载输出，凸轮轴齿轮驱动侧产生的啮合力明显高于背隙侧产生的啮合力。

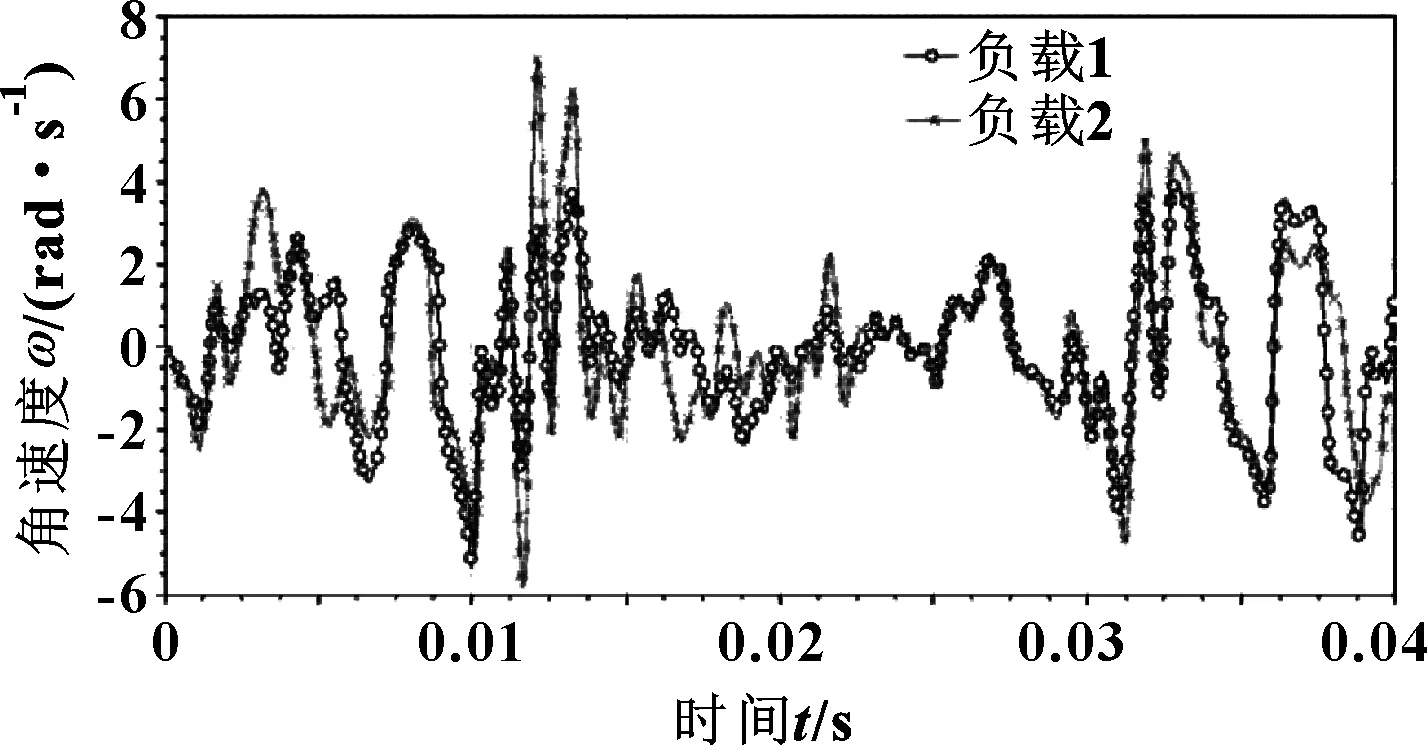
图5 凸轮轴齿轮角速度

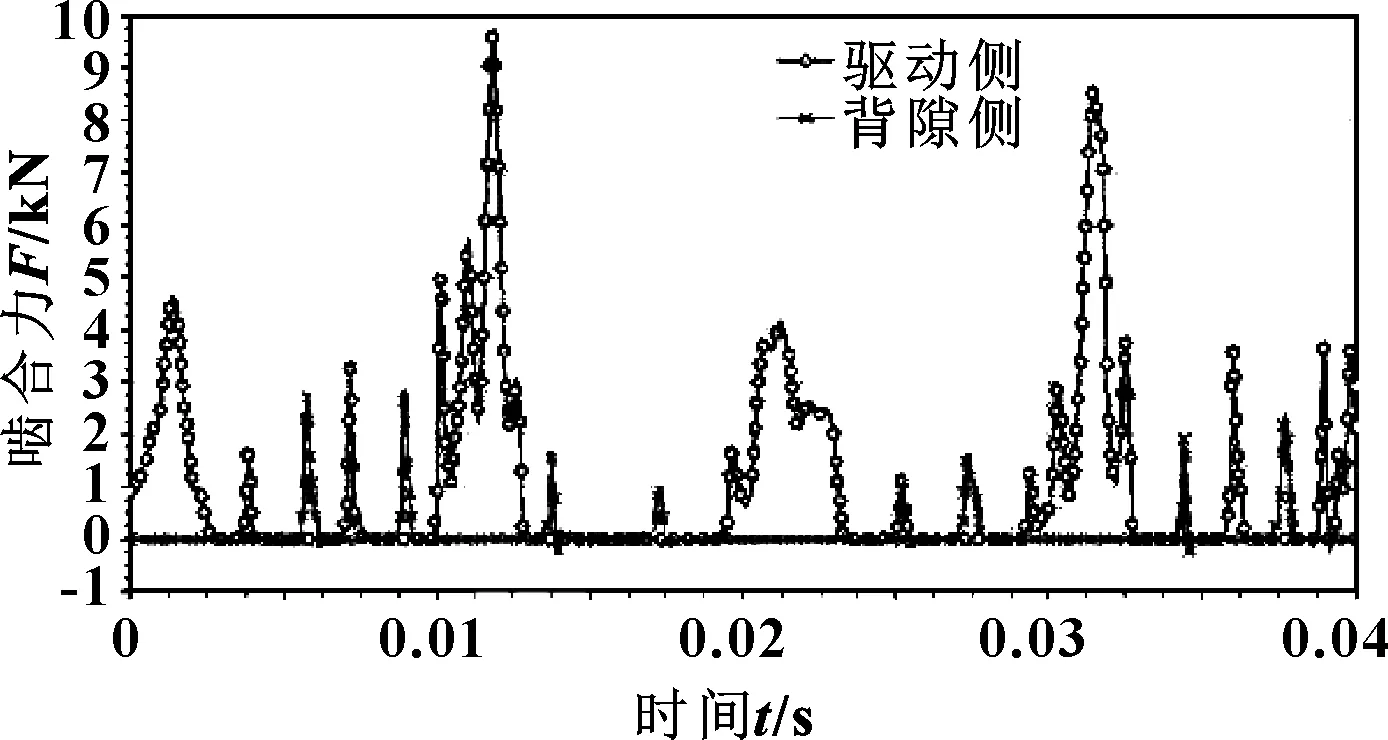
图6 加负载1时凸轮轴齿轮与惰轮啮合力

图7 加负载2时凸轮轴齿轮与惰轮啮合力

由图8—10可以看出：负载增大对惰轮角速度及啮合力曲线无明显影响，但峰值位置依然受负载峰值的影响；加负载2时惰轮角速度峰值与啮合力峰值均远小于凸轮轴齿轮，惰轮角速度波动也相对平稳；由于无直接外界负载作用，惰轮驱动侧与背隙侧啮合力差距不明显。

图8 复合惰轮角速度

图9 加负载1时惰轮与曲轴齿轮啮合力

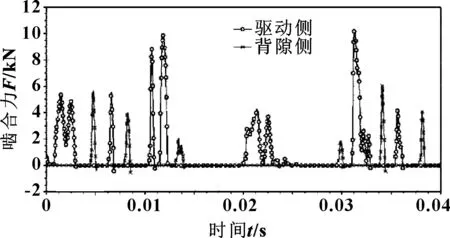
图10 加负载2时惰轮与曲轴齿轮啮合力

综上所述，负载扭矩的增大对凸轮轴齿轮的角速度与啮合力均有较大影响，且角速度与啮合力峰值位置与负载扭矩峰值位置相近；负载扭矩的增大对复合惰轮角速度与啮合力无影响，但角速度与啮合力峰值位置依然受负载峰值的影响。

2.2 曲轴转速波动对动力学影响

图11所示为凸轮轴齿轮角速度变化曲线。可以看出：在不加载曲轴转速波动时，角速度峰值绝对值为5.87 rad/s，加载曲轴转速波动时角速度峰值绝对值为6.95 rad/s，且在加载曲轴转速波动的情况下，角速度波动明显增大。图12所示为凸轮轴齿轮与复合惰轮的啮合力变化曲线。可以看出：在加载曲轴转速波动的情况下，啮合力峰值增大，相较于不加载曲轴转速波动增大了近2 000 N；另外，由于背隙与弱阻尼的存在，使得啮合力曲线不是完全周期性变化的。综上所述，曲轴转速波动对齿轮传动系统动力学结果造成了不可忽略的影响，因此在进行齿轮传动动力学分析时，考虑曲轴转速波动的影响更有利于动力学分析的准确性。

图11 齿轮角速度

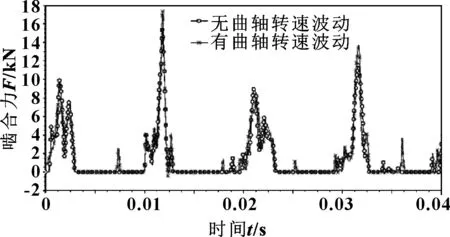
图12 齿轮啮合力

3 内部激励对正时齿轮传动系统动力学影响

文中内部激励主要分析不同齿侧间隙对齿轮动力学的影响。在齿轮传动过程中，齿廓之间需要一定的润滑油膜来避免齿轮发热膨胀而卡死，齿廓之间就需要留有间隙[11]。但是齿侧间隙的存在会导致齿轮之间的冲击，造成传动过程中的振动。另外，在齿轮的生产加工以及安装过程中都会存在一定的误差，尤其是齿轮传动过程中产生的磨损，都使得齿轮啮合不可避免地存在间隙[12]。目前柴油机的正时齿轮传动系统齿侧间隙一般控制在0.05～0.35 mm之间[13]，文中分析了齿侧间隙分别为0.1、0.2、0.3 mm时，对凸轮轴齿轮角速度、啮合力的影响，结果如图13、14所示。

图13 不同齿侧间隙时齿轮角速度

图14 不同齿侧间隙时齿轮啮合力

由图13可以看出：随着齿侧间隙数值的不断增大，角速度幅值相应地增大，最大峰值依次为5.46、6.95、9.96 rad/s；齿侧间隙为0.3 mm时，角速度峰值与波动明显增大，可见较大的齿侧间隙容易造成齿轮啮合过程的振动。由图14可以看出：随着齿侧间隙的增大，驱动侧啮合力峰值相应增大，最大峰值依次为15 039.8、17 370.4、19 663.2 N。可见，增大齿侧间隙数值，齿轮加速冲击的空间相应变大，齿轮冲击状态也就越明显；齿侧间隙从0.1 mm增大到0.3 mm过程中，啮合力相位有一定的后移，后移的时间是齿侧间隙变大导致了齿轮靠近时间的增长。综上所述，齿侧间隙越大越容易导致齿轮啮合过程中的振动与冲击，但齿侧间隙过小又会造成加工难度的增大及成本的增加，因此需要适当地减小齿侧间隙。

4 结论

(1)负载扭矩的增大对凸轮轴齿轮的角速度与啮合力均有较大影响，且角速度与啮合力峰值位置与负载扭矩峰值位置相近。负载扭矩的增大对复合惰轮角速度与啮合力无影响，但角速度与啮合力峰值位置依然受负载峰值位置的影响。

(2)曲轴转速波动对齿轮传动动力学结果造成了不可忽略的影响，因此在进行齿轮传动动力学分析时，考虑曲轴转速波动的影响更有利于动力学分析的准确性。

(3)齿侧间隙越大越容易导致齿轮啮合过程中的振动与冲击，但齿侧间隙过小又会造成加工难度的增大及成本的增加，所以需要适当地减小齿侧间隙。