基于FASTA结合p-指数阈值降噪法的MCA方法对车轴应变信号处理的研究
2019-04-20张子璠陈晓洁吴宇星
张子璠,李 强,陈晓洁,吴宇星
(北京交通大学 机械与电子控制工程学院,北京 100044)
车轴是轨道车辆承载的关键部位,直接起到轨道与构架载荷的传递作用[1]。随着车辆运行速度的不断加快,车轴与轨道之间产生的相互作用力呈指数型增长,因此实现车轴受力的精确测量进而编制高置信度的车轴载荷谱是车轴结构可靠性设计的基础。但在实际线路测试中,车轴应变信号会受到外界因素的干扰从而产生噪声,因此需要在保证信号能真实反映车轴受力状态的前提下,尽可能排除噪声对其干扰[2]。
工程信号处理方法得到了大力发展,例如小波变换、希尔伯特黄变换和双树复小波变换[3],这些方法基于不同的中心频率和带宽分解信号。然而,车轴应变信号及其干扰信号可能拥有相似的中心频率及重叠的带宽,因此上述办法不适用于车轴应变信号噪声的去除。
为此,Stark等人[4]提出了形态分量分析(Morphological Component Analysis, MCA)方法。在MCA方法中,Stark采用了迭代软阈值算法(Iterative Soft Thresholding Algorithm, ISTA)获得最优解,但ISTA缺点在于只有线性收敛速度,效率低。因此,学者们相继提出了不同的改进算法。Bioucas-Dias等人[5]提出了二阶段软阈值算法(Two-Step Iterative Shrinkage/Thresholding Algorithm,TwIST),并证明了TwIST拥有比ISTA更快的收敛速度。Beck等人[6]提出了快速迭代软阈值算法(Fast Iterative Soft Thresholding Algorithm, FISTA),该算法不但保持了ISTA的简洁性,并且拥有高阶全局收敛速度,数值模拟结果也充分证明了算法在降噪效果上的优越性。Goldstein等人[7]在FISTA的基础上提出了快速自适应收缩阈值算法(Fast Adaptive Shrinkage Thresholding Algorithm, FASTA),该算法在FISTA的基础上引进了自适应步长策略,大幅度提高了计算效率,仿真证明了FASTA在目前的改进算法中具有最快的收敛速度。
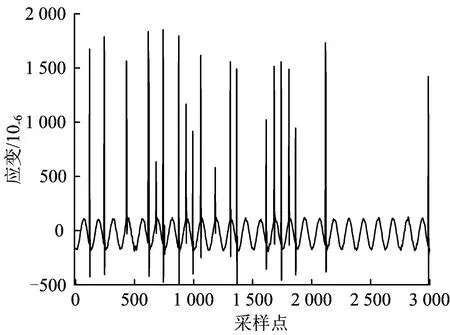
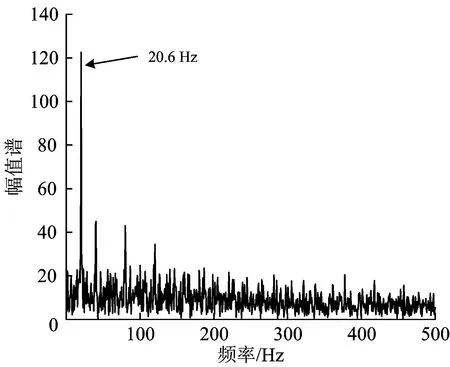
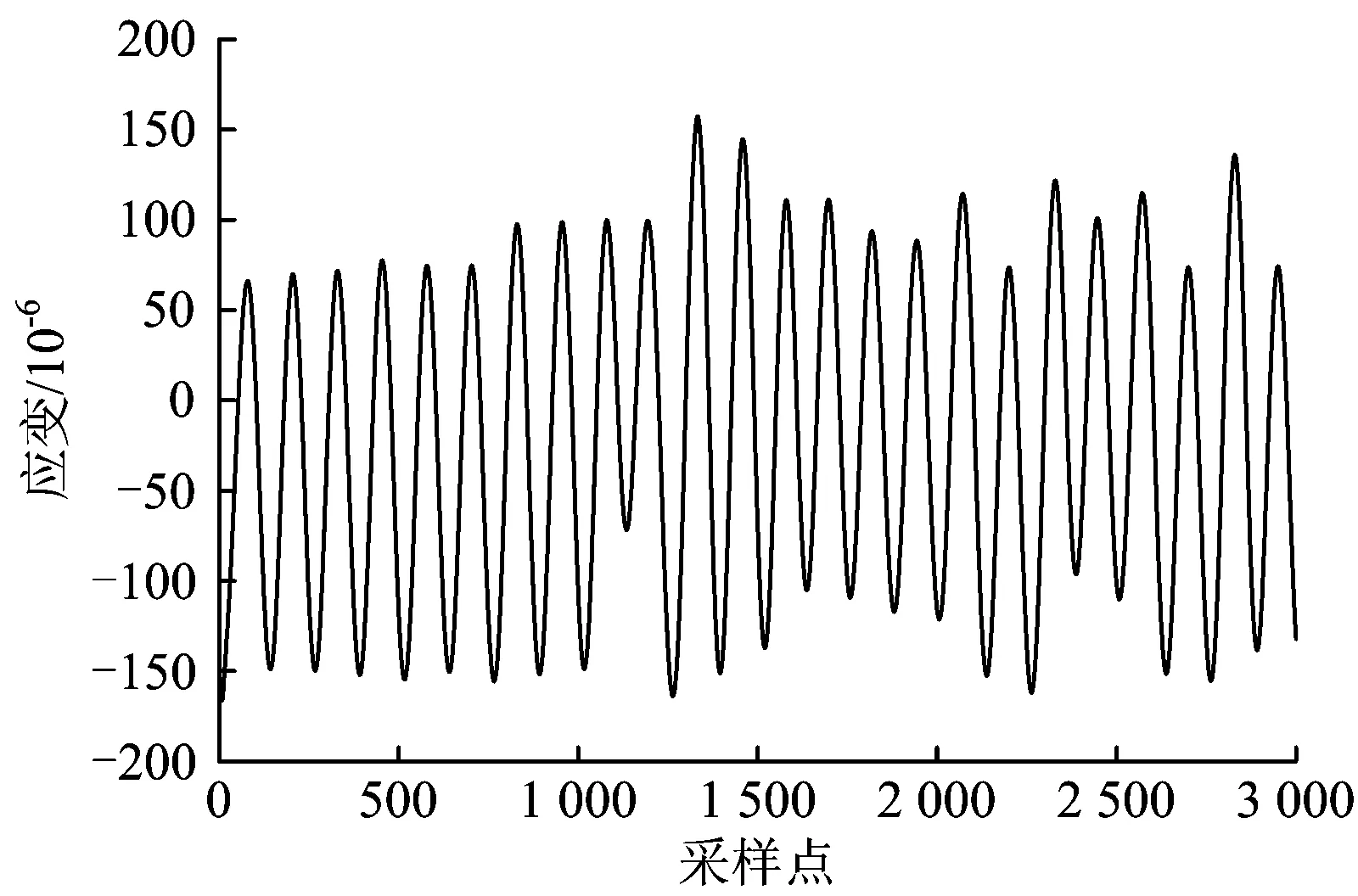
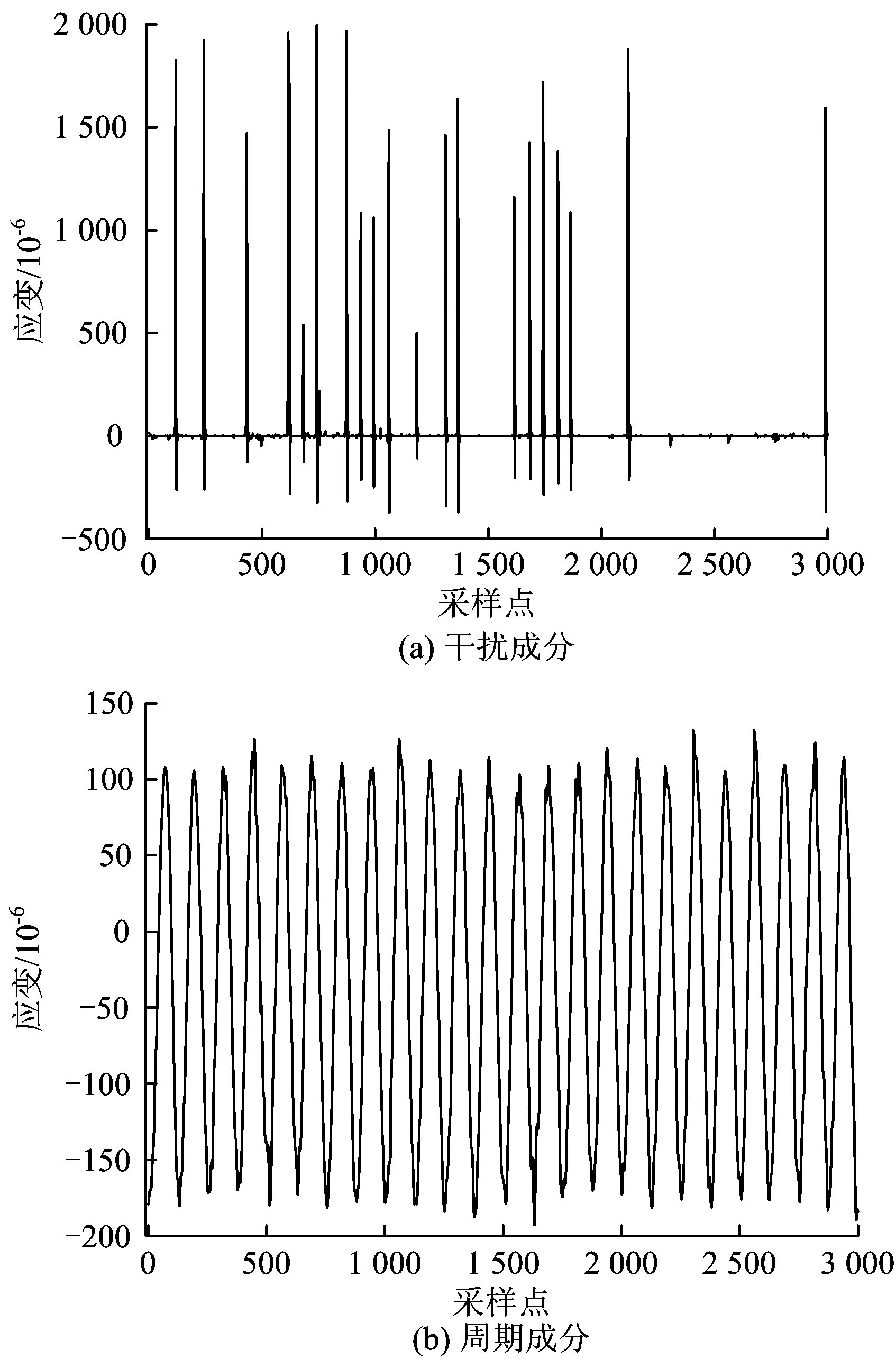
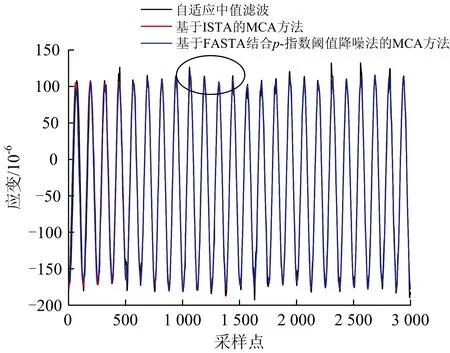
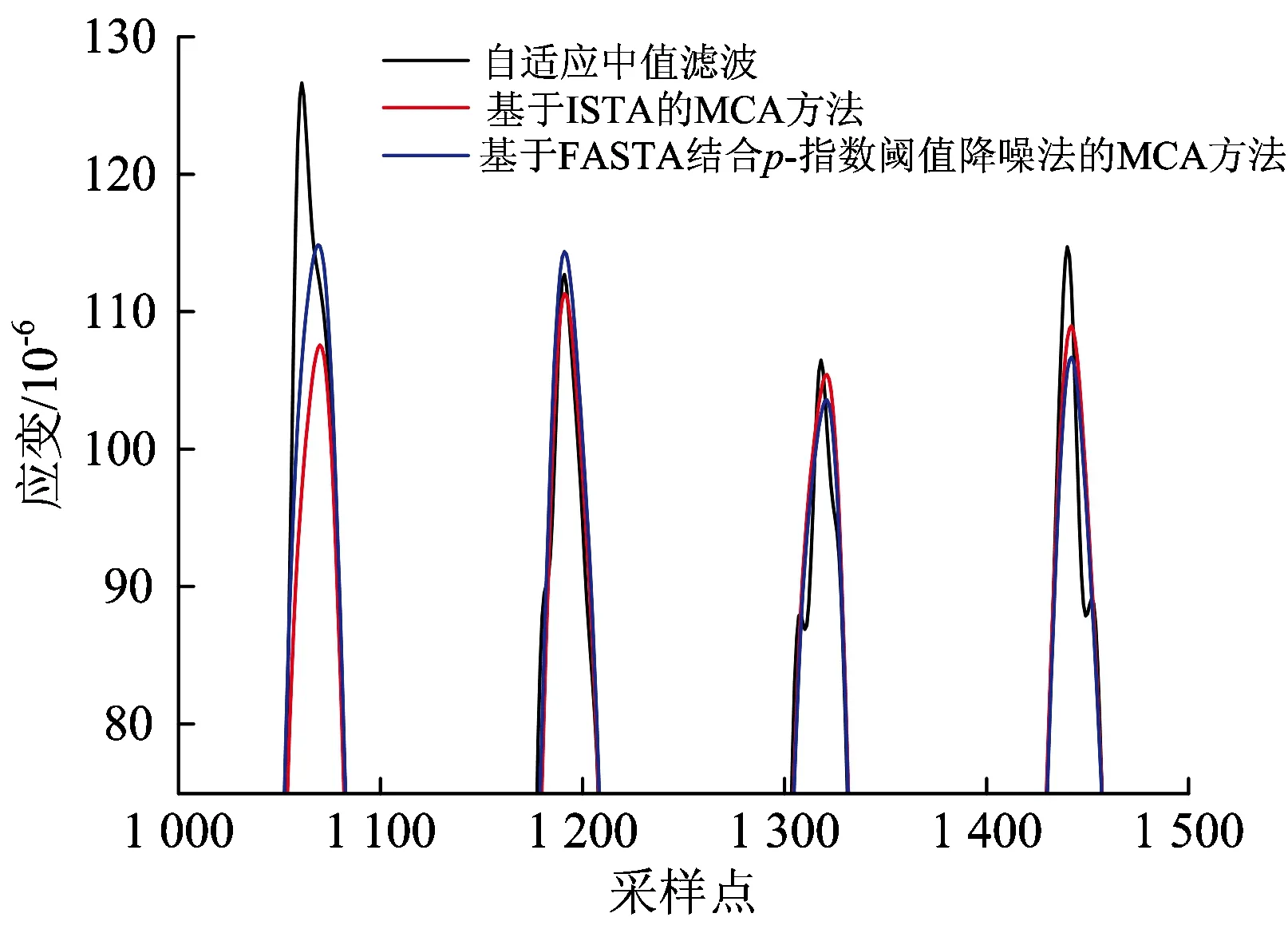
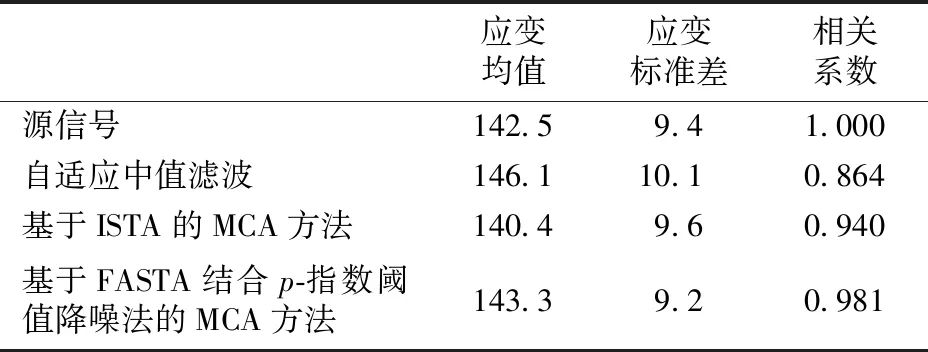
上述算法在迭代过程中采用了软阈值降噪法对信号进行降噪处理,但是软阈值降噪法的结果偏差较大,去除噪声的同时会削弱源信号,效果不理想。针对软阈值降噪法的缺点,不同的改进降噪法相继被提出。Blumensath等人[8]提出了硬阈值降噪法,但由于收缩函数在零点的不连续性从而会使结果产生较大的方差。Bobin等人[9]提出最大—平均机制改善了降噪效果,并证明了硬阈值比软阈值拥有更好的降噪水平。Gao等人[10]针对以上2种降噪方法的缺陷,提出了新的半软阈值降噪法,结果表明半软阈值法降噪效果更优越,但是由于该方法中需要估计2个阈值,方法复杂度也大大提升。随后,Chartrand等人[11]证明了阈值算子可以统一为p-伪范数阈值算子,其中p(0 本文基于FASTA和p-指数阈值降噪法在计算效率和降噪效果上的优势,将2种算法相结合并应用到MCA方法中,分析采用该方法对车轴应变信号降噪的原理,并通过仿真和实测验证其可行性和有效性。 在求解稀疏系数的过程中,MCA方法的基本思想是,根据稀疏约束正则化的原则,求解形如式(1)的最优化问题,以得到每个成分si的最稀疏表示。 min:‖φiαi-si‖2+λ‖αi‖1 (1) 式中:λ为正则化参数,用来调节每个分量的稀疏程度;‖·‖2为向量的2范数;‖·‖1为向量的1范数。 (2) 其中, η=λτk 当列车以恒定速度160 km·h-1行驶时,车轴应变信号的中心频率为16 Hz,同时有微弱的高次谐波,故可认为该信号为单一频率的类正余弦波形。当信号受到外部干扰时,会出现明显尖峰状脉冲干扰,通过频谱分析可知,干扰频率与源信号中心频率并无重合,故传统意义上的滤波可以去除干扰,但由于车轴应变信号存在高次谐波,将对源信号造成一定损伤,使得后期进行载荷谱编制时会出现偏差。 由于车轴应变信号由以转频及其谐波为主要成分的周期成分以及干扰成分组成。这2种成分在形态表现上存在显著差异,因此,可根据周期成分与干扰成分之间的差异性,利用MCA方法实现车轴应变信号噪声即干扰成分的去除。基于MCA的车轴应变信号干扰成分去除步骤如下。 (1)对于信号中的周期成分,构建局部离散余弦变换(Local Discrete Cosine Transform, LDCT)字典用于其稀疏表示,对于信号中的干扰成分,构建8阶消失矩Symlet小波字典用于其稀疏表示;阈值更新准则选取线性递减;综合考虑计算效率和结果精度,迭代次数取100;阈值最小值根据信号中噪声的标准差确定,而标准差可以由中值绝对偏差策略获得,即 (3) (2)利用基于FASTA结合p-指数阈值降噪法的MCA方法对车轴应变信号进行分析,得到周期成分和干扰成分的稀疏系数并进行重构,即可实现车轴应变信号噪声的去除。 基于FASTA结合p-指数阈值降噪法的MCA方法用于车轴应变信号处理的流程如图1所示。 图1 基于FASTA结合p-指数阈值降噪法的MCA方法用于车轴应变信号处理流程图 首先,验证FASTA结合p-指数阈值降噪法在计算效率上的优越性。随机生成(1 000×1)维、稀疏度为10的向量,使用100×1 000型随机矩阵进行压缩得到(100×1)维观测向量,分别使用ISTA,FISTA,FASTA结合p-指数阈值降噪法进行源信号重构。仿真中记录每个算法的计算时间,用以衡量算法复杂度,运行时间见表1。由表1可知:FASTA结合p-指数阈值降噪法在收敛速度上明显优于传统的ISTA,运行时间减少约61.5%,由于采用了自适应步长的选择策略,FASTA结合p-指数阈值降噪法的收敛速度也显示出比FISTA更快的优势,运行时间比后者减少约46.4%。目标函数的收敛情况对比如图2所示。由图2可见:采用ISTA在第50次迭代时得到的目标值采用FASTA结合p-指数阈值降噪法在第10步迭代就能得到,收敛速度提高近5倍,FISTA在第20步得到的目标值改进算法在第10次迭代得到,收敛速度提高近1倍;仿真证明了FASTA结合p-指数阈值降噪法在计算效率上有极大优势。 表1 算法计算时间对比 图2 算法收敛速度对比 其次,验证基于FASTA结合p-指数阈值降噪法的MCA方法对车轴应变信号中干扰成分的去除效果。给出由脉冲信号以及频率为30.5 Hz的正弦信号x(t)=sin(2π×30.5×t)(t为采样时刻)组成的2路复合仿真信号作为源信号输入,分别用来模拟车轴应变信号中的干扰成分和周期成分。工程上通常使用α稳定分布描述脉冲信号,α∈(0,2],α越小,脉冲性质越显著,仿真中设α=1.2。采样频率为1 000 Hz,峰值信噪比为20 dB,采样时间为2.048 s。仿真得到车轴应变信号的周期成分和干扰成分后,随机生成1个2×1型混合矩阵将仿真信号进行合成得到混合信号,构成车轴应变信号的源信号如图3所示。 使用基于FASTA结合p-指数阈值降噪法的MCA方法对混合信号进行处理,根据信号中周期成分和干扰成分的形态特点,稀疏字典选择局部离散余弦变换字典和8阶消失矩Symmlet小波字典,分别用来匹配混合信号中的周期成分和干扰成分,分离后的车轴应变重构信号如图4所示。通过对比源信号周期成分与重构信号周期成分的时域波形可知,重构信号与源信号幅值大小一致,未发生变形,证明了算法可以有效将周期成分同干扰成分分离,并且重构周期成分已基本不含噪声,提高了信噪比。 图3 车轴应变源信号 最后,验证基于FASTA结合p-指数阈值降噪法的MCA方法的鲁棒性。好的信号处理方法需要尽量不受噪声的影响。选取最小均方误差作为衡量车轴应变的源信号与重构信号之间重构质量的评价指标。最小均方误差值越小,表明信号重构的质量越高。信噪比为5~30 dB时基于不同算法的MCA方法最小均方误差值随信噪比的变化情况如图5所示。由图5可见,基于FASTA结合p-指数阈值降噪法的MCA方法的最小均方误差受信噪比影响较小,且明显低于基于ISTA的MCA方法,表明前者在信号重构质量方面相较于后者具有更好的鲁棒性。 图4 车轴应变重构信号 图5 重构信号的最小均方误差 为了验证基于FASTA结合p-指数阈值降噪法的MCA方法用于去除车轴应变信号中脉冲干扰的有效性,选取某型动车组线路实测数据进行测试。 试验中,在车轴的7个关键断面处安装应变片,组桥用于测量垂向力。车轴贴片截面位置的选取如图6所示。 在图6所示的每个关键截面上,每相隔90°布置2个应变传感器,方向为轴向,共计8个,以A截面为例,其贴片位置如图7(a)所示。其中,对向的2组传感器组成1个惠斯通全桥,因此每个截面有2个全桥j1和j2(j=A,B,C,D,E,F,G)。由于在恒定载荷作用下,1个全桥的输出电压为轮对转角的周期函数,同一截面不同全桥输出电压Uj1和Uj2仅在相位上相差90°,为保证每个截面输出电压为一稳定值,不随时间变化。截面综合输出电压Uj为 (4) 图6 车轴贴片截面(单位:mm) 图7 车轴截面贴片位置及组桥方案示意图 其中, 式中:L为电阻式应变片的转换系数;UE为电桥输入电压;θ为轮对转角;a和b为对每个截面4个传感器采集到的应变做傅里叶级数展开得到的傅里叶系数;φ为傅里叶级数展开的初相位。 得到截面输出电压后,即可根据电压—应变转换系数得到相应截面的综合应变。 由于车辆电气设备对车轴应变信号采集设备造成电磁干扰,车轴应变信号中普遍长时间存在脉冲干扰,因此如不能有效去除脉冲干扰,将会对车轴载荷谱的编制造成较大误差。 假设列车行驶速度为v(km·h-1),车轮滚动圆直径为D(m),则车轮旋转1周的时间T=3.6πD/v,旋转频率f=v/3.6πD。不同速度对应的前7次奇次输出频率见表2。由上述理论分析可知,对于时速160 km·h-1列车车轴信号而言,几乎不存在1倍频以外的高次谐波。实测车轴信号应变信号时域波形如图8所示。为方便示意,从实测的受干扰信号中截取3 000个采样点,得到其频谱图如图9所示。由图8可见,车轴应变信号受到了严重脉冲干扰。由图9可见,车轴应变信号频谱中出现了大量1倍频之外的噪声频率。 表2 速度及输出倍频 图8 实测车轴应变信号时域波形 图9 实测车轴应变信号频谱图 对车轴实测应变信号进行16.5 Hz的低通滤波,结果如图10所示。由图10可见,源信号出现脉冲干扰的时刻,低通滤波后重构信号波形出现较大畸变,源信号未出现脉冲干扰的时刻,重构信号存在均值漂移的情况,证实了传统的滤波方式无法有效去除脉冲干扰。 采用基于FASTA结合p-指数阈值降噪法的MCA方法对源信号进行脉冲降噪处理,根据上文分析,车轴应变信号周期成分成正弦波形式,构建局部离散余弦变换字典进行匹配,此外由于小波基对信号脉冲有着较好的匹配能力,构建8阶消失矩Symlet小波字典对干扰成分进行稀疏表示。重构信号周期成分和干扰成分如图11所示。由图11可见,重构的周期成分在源信号出现脉冲干扰的时刻,波形并未出现畸变,且均值与源信号一致,没有出现漂移的现象,证明了基于FASTA结合p-指数阈值降噪法的MCA方法能够在不损伤车轴应变信号周期成分的前提下,有效地去除脉冲干扰。 图10 低通滤波信号波形图 图11 MCA方法得到的车轴应变重构信号波形 为进一步说明基于FASTA结合p-指数阈值降噪法的MCA方法在去除车轴应变信号中脉冲干扰效果上的优越性,选取基于ISTA的MCA方法以及目前工程上常用的自适应中值滤波算法进行降噪效果对比,结果如图12所示。由图12可见,重构信号波形差异不明显,表明3种方法均可以有效去除信号中的脉冲干扰。 图12 3种方法降噪信号波形图 选取图12所示位置源信号中存在脉冲干扰的时刻进行局部放大,放大波形如图13所示。由图13可见,3种方法中基于FASTA结合p-指数阈值降噪法的MCA方法与基于ISTA的MCA方法并未在出现干扰的时刻发生波形畸变,而自适应中值滤波效果较差,仍存在一定程度的变形;但3种方法在未出现干扰的时刻均较好地保留了源信号形貌。 图13 脉冲干扰时刻波形局部放大图 列车匀速行驶时,车轴各截面的综合应变近似不变,因此可将不同方法得到的处理信号结果其均值与标准差作为重构质量的评判标准。此外,也可采用同一截面、同一时间的源信号与重构信号间的相关系数作为重构质量评判标准。相关系数为 (5) 将处理后的重构信号和同一截面另一通道的源信号依据式(4)进行计算求得截面综合应变,并与通过源信号(同一路况、同一车速下测得)计算得到的截面综合应变的对比结果见表3。由表3可知,由FASTA结合p-指数阈值降噪法处理后得到的综合应变均值和标准差更接近源信号计算结果,误差相比自适应中值滤波和基于ISTA的MCA方法分别降低77.4%和55.5%,相关系数则分别提高13.5%和4.4%,证明了方法用于去除脉冲干扰的可行性和有效性。 表3 重构质量评判标准 针对基于ISTA的MCA方法收敛速度慢降噪效果差的缺点,将FASTA结合p-指数阈值降噪法引入到MCA方法中,根据车轴应变信号与干扰信号的形态特点,分别构建局部离散余弦变换字典和小波基字典进行成分的稀疏表示,从而达到去除轨道车辆车轴应变信号中脉冲干扰的目的。仿真车轴应变信号处理结果表明,基于FASTA结合p-指数阈值降噪法的MCA方法实现了混叠信号中不同形态分量的分离,在收敛速度上要优于基于ISTA的MCA方法,并且有更好的鲁棒性。实测车轴应变信号处理结果表明,基于FASTA结合p-指数阈值降噪法的MCA方法能有效分离车轴应变信号中的脉冲干扰成分,并且重构信号与源信号的相关系数高于基于ISTA的MCA方法以及自适应中值滤波方法,提供了车轴应变信号处理的一种有效方法。1 基于FASTA结合p-指数阈值降噪法的MCA方法
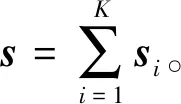
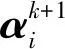
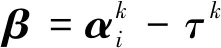

2 车轴应变信号降噪原理
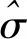
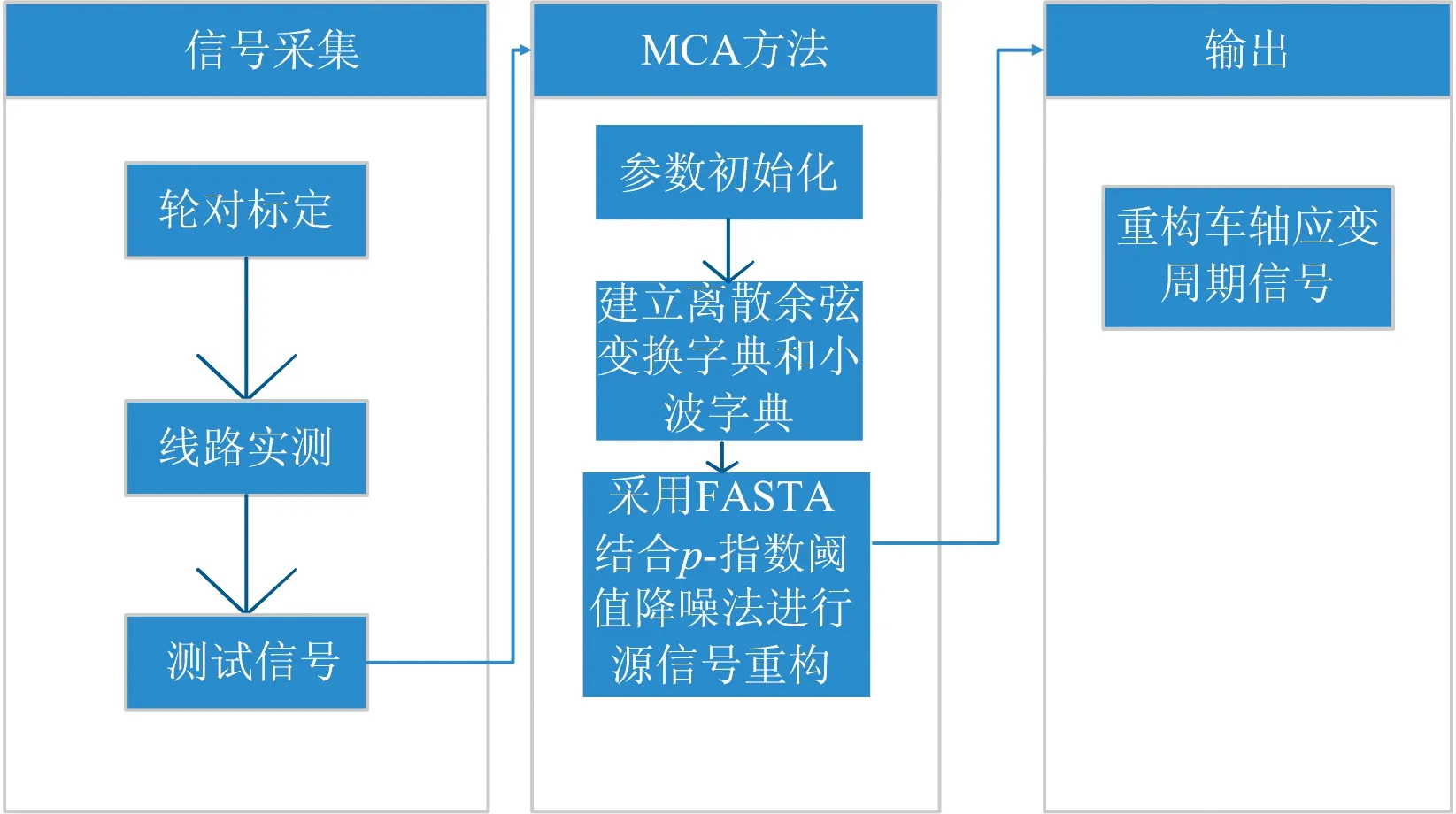
3 仿真验证

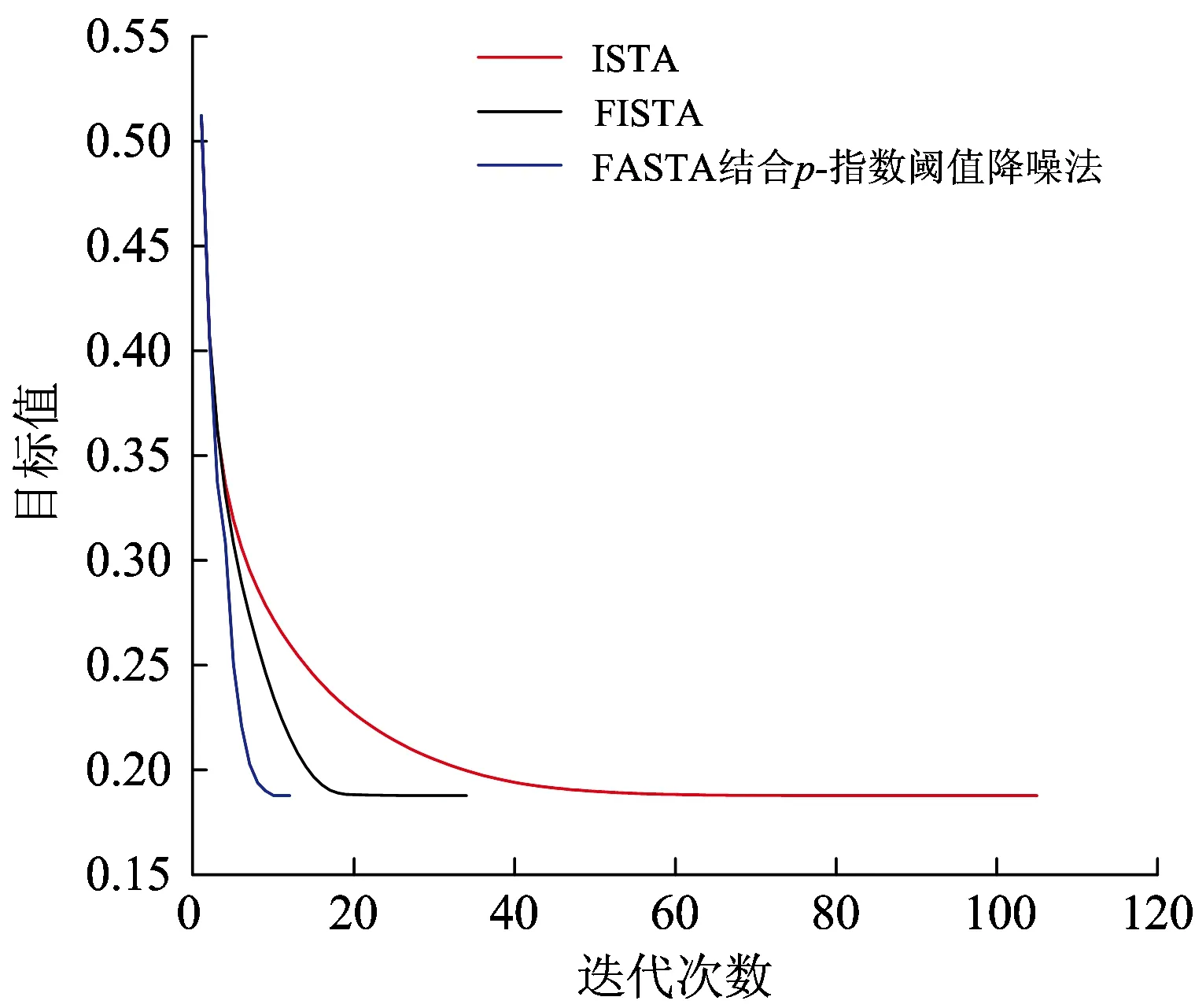
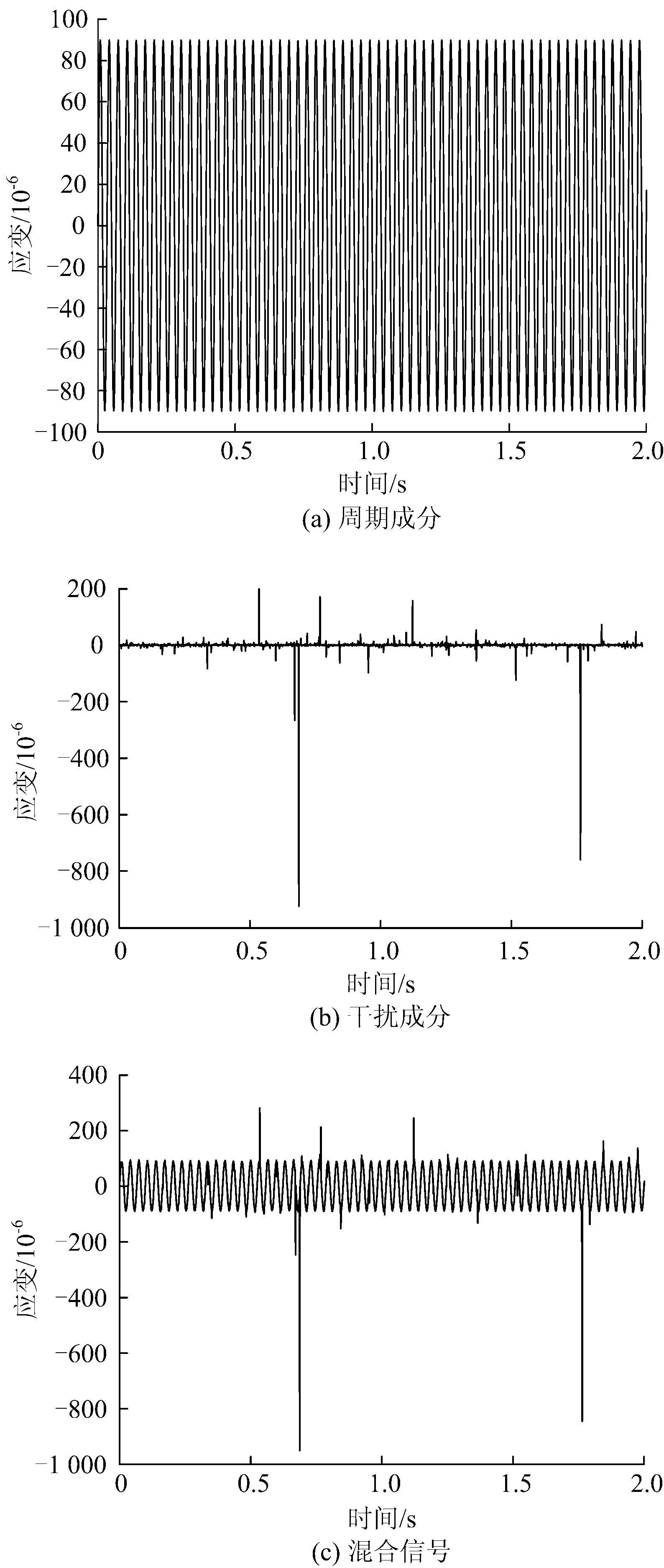
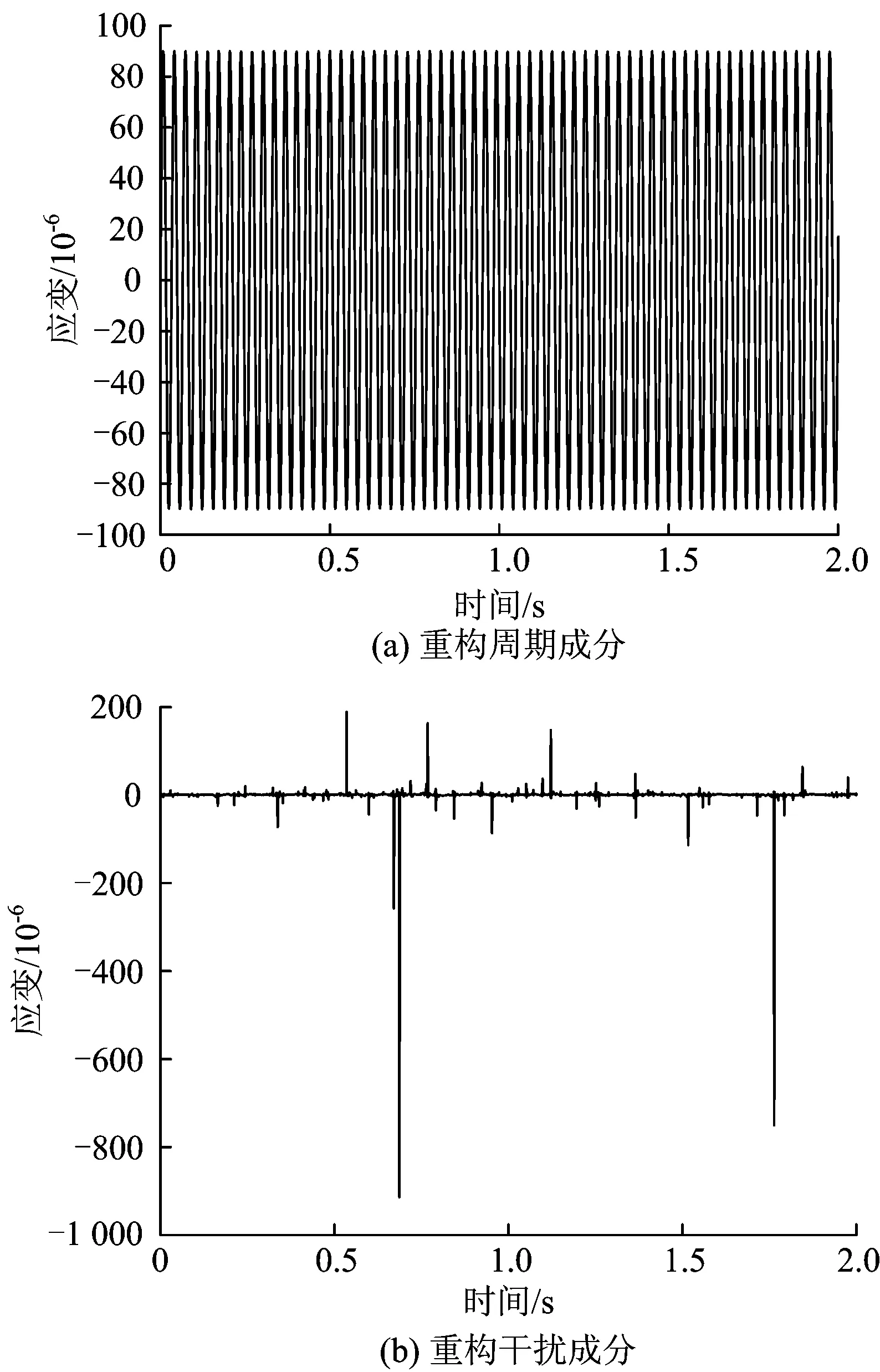
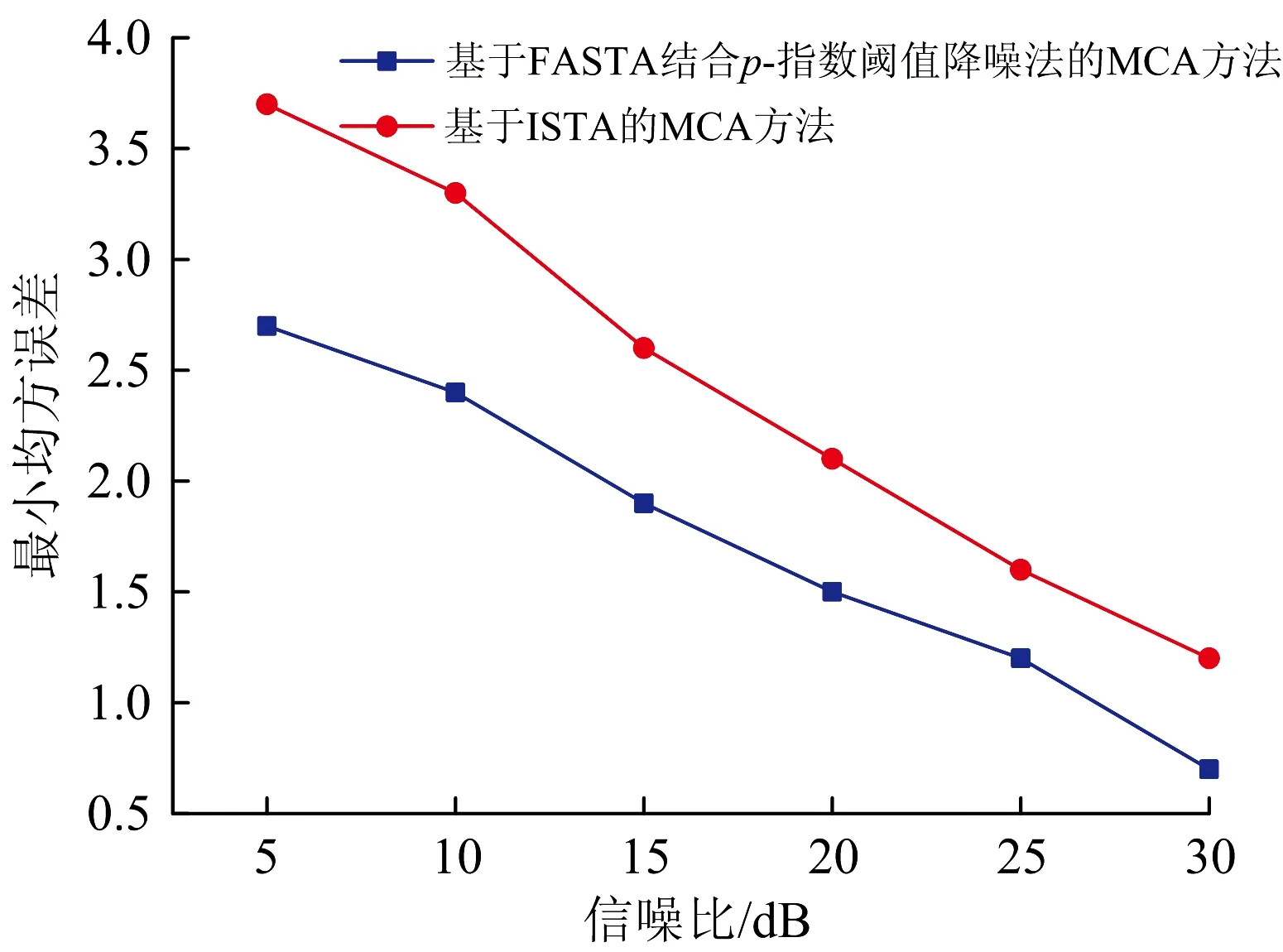
4 实例验证
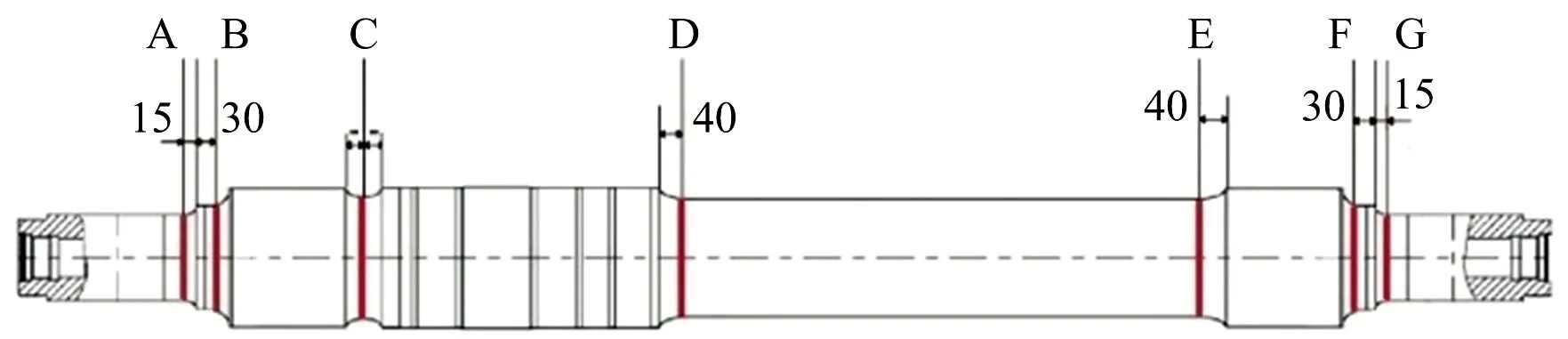
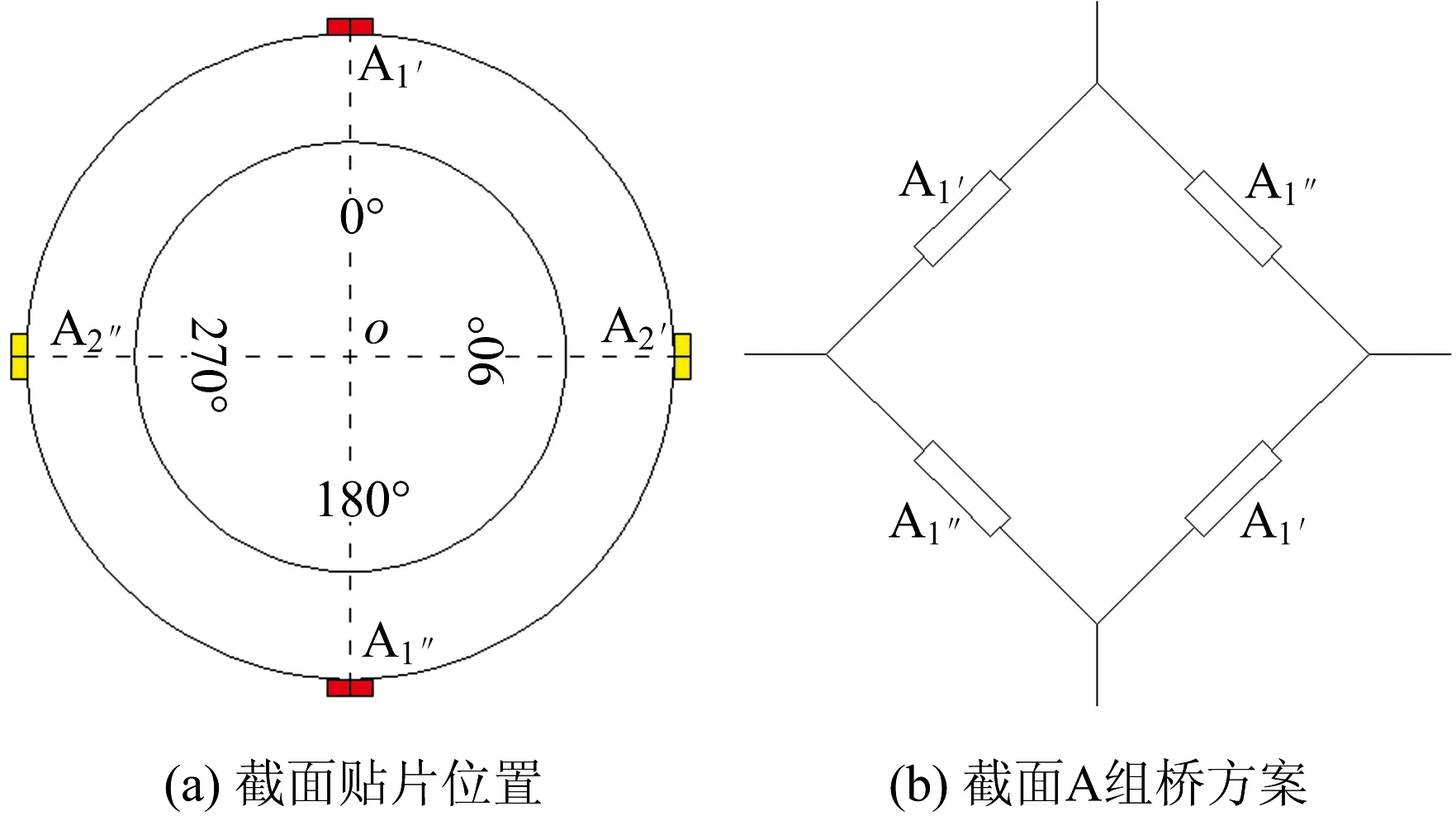
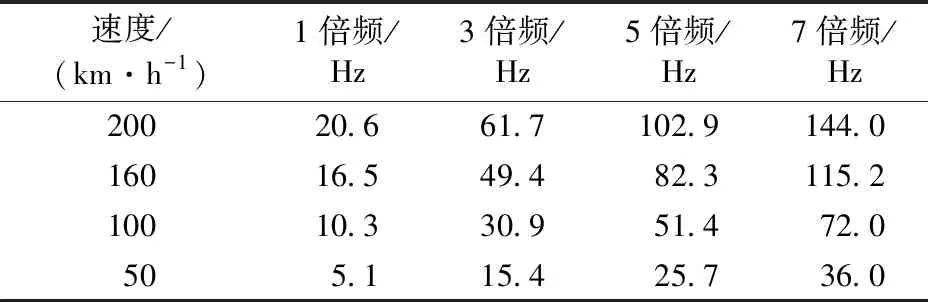
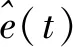
5 结 语
