滑坡动力失稳定量分析

王 翔，乔春生，马晓鹏

(1.北京交通大学 土木建筑工程学院，北京 100044； 2.西南交通大学 土木工程学院，四川 成都 610031)

滑坡的地震响应研究，一般集中在研究滑坡的动力稳定性。主要分析方法有拟静力法[1-2]、Newmark分析法[3-5]、动力有限元时程分析法[6-8]等。拟静力法原理简单，其稳定性系数指标概念清晰，在设计中应用最为广泛，积累了较多的使用经验。拟静力法的缺点是将瞬时作用的地震荷载当成永久荷载，计算结果过于保守。Newmark分析法在坝坡动力稳定性研究中，考虑到滑动体在地震中受惯性力作用而运动或停止的规律，从刚体位移计算角度，计算滑动体可能发生的永久位移。这类方法的最大不足是缺乏变形的临界破坏标准。动力有限元时程分析法，按时刻将瞬时动应力假定为静应力，计算瞬时安全系数，从而得到安全系数的时程曲线。

稳定性分析方法能得到边坡的稳定性系数，有利于认识边坡的整体稳定性程度。但是，单一的稳定性系数不能分析边坡破坏的过程和原因，无法描述边坡的渐进破坏过程，以及各部分的稳定性差异。为此，需要开展边坡地震破坏机理研究。目前多采用定性描述的方法[9-10]，即通过现场调查，对地震所造成的边坡破坏过程及规律进行总结。即或进行定量描述，也是通过数值模拟，从应力或位移的分布特征和演化发展方面进行描述[11-13]。

通过稳定性系数，能够直观判断边坡的整体稳定性状态，便于了解边坡的整体安全储备，并指导支护设计。边坡滑动机理的分析，则可以认识边坡的渐进失稳过程和局部稳定性，使支护设计具有针对性，更加优化。然而目前通过定性或通过应力位移定量描述滑坡滑动机理不具有直观性，不便于设计应用。基于此，本文在定义滑带单元点安全系数和整体安全系数的基础上[14-15]，计算出瞬时点安全系数，根据点安全系数在滑带上的空间分布规律及动力时程演化定理分析滑坡的动力失稳。

1 滑坡点安全系数计算

在传统的滑坡动力稳定性分析中，滑坡稳定性系数是针对整个滑坡体而言的，可称为整体稳定性系数。但是滑坡在动力失稳过程中，一般不会出现突发性的整体失稳滑移，而是具有渐进破坏特性。即滑坡体首先出现局部部位的失稳，然后滑面逐渐发展形成，最终导致滑坡整体失稳滑移。也就是说，滑体各部分的失稳滑移有一定的先后顺序。滑坡的这种渐进失稳破坏特性，一般称为滑坡的滑动机理。从变形破坏模式的角度，常将滑动机理分为整体式、牵引式和推移式等类别[16]。这只是定性的做法，为了定量描述滑坡的动力失稳机理，可以定义滑面点安全系数。在三维数值计算中，将滑带离散成八节点六面体单元，赋予材料参数和边界条件，计算出计算域的应力场和位移场，继而根据滑带应力状态和滑动趋势计算点安全系数。根据点安全系数在滑面上的分布判断滑坡滑动机理，并将滑带点安全系数对滑带面积加权平均，得到滑坡的整体安全系数[15，17]。

点安全系数计算时，不失一般性，应力强度准则采用摩尔—库仑剪切屈服准则，即

τu=σtanφ+c

(1)

式中：τu为滑面抗剪强度；σ为滑面正应力；c和φ分别为滑带土的抗剪强度参数黏聚力和内摩擦角。

确定出计算单元中心位移矢量U，由于八节点六面体应力单元有8个节点，因此U的分量(Ux，Uy，Uz)可表示为

(2)

式中：Ux,i，Uy,i和Uz,i分别为节点位移分量。

设计算单元处滑面的法向量为n，为求单元中心位移矢量在滑面S上的投影向量u，可用下式表示

u=(n×U)×n

(3)

u也就是滑带单元中心的实际滑动方向向量。

数值分析获得滑带单元应力状态后，按弹性力学空间应力分析法，对于滑面S，可计算得到面上的法向应力分量σn，以及滑动方向u的剪应力分量τ。单元点安全系数FE定义为

(4)

工程中习惯于采用整体安全系数评价滑坡的稳定性，因此，可以采用点安全系数对滑面面积的加权平均值作为整体安全系数F3D，即

(5)

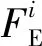
2 地震滑坡动力失稳定性分析

以青海省玉树机场路2#滑坡为例，研究滑坡动力失稳的分析方法。

2.1 地震滑坡概况

2010年4月14日，青海省玉树县结古镇西侧发生7.1级大地震，强烈的地震动造成了多处地震滑坡，其中国道214线K822+888—K824+400段就发生了滑坡群。滑坡群分布在线路右侧，成带集中分布且具有较大的规模。滑坡造成了较严重的工程危害，例如西杭电站引水渠位于滑坡体上，出现了多处裂缝和局部垮塌。滑坡堆积物位移到机场公路上，造成了公路阻断。对机场高速公路的运营安全造成了严重威胁。

滑坡群中，K823+118—K823+600段编号为2#滑坡，滑坡性质属于堆积层滑坡。该滑坡体为山前洪积物，坡面平缓，自然坡度10°左右。滑坡前后缘高差70 m，后缘位于高程3 774 m附近，前缘在路基面处，属于河流相的一级阶地。根据滑坡体在地震过程中产生的变形迹象和自然的地形地貌，可确定该滑坡的主滑动方向为NE46°，与线路近似垂直。从规模上看，滑坡体在主滑方向上的纵向长度约317 m，平行路线方向宽度约482 m，滑体最厚处22.80 m，滑坡体积约289万m3。该滑坡为分级滑坡，前级分布在西杭电站引水渠与线路之间，后级位于引水渠内侧与后山之间。图1为滑坡平面图，图2为主轴剖面。

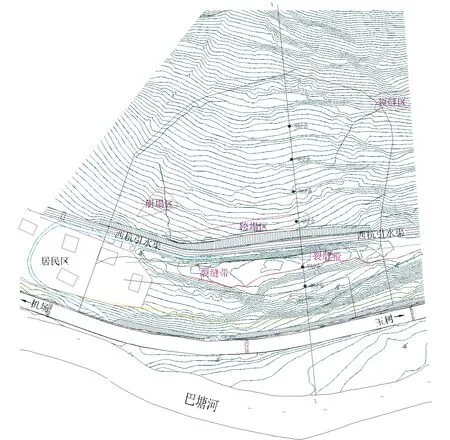
图1 2#滑坡平面图

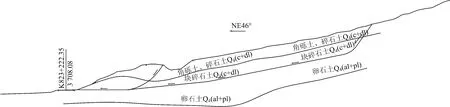
图2 滑坡主轴剖面

2.2 动力失稳的定性分析

滑坡分布在巴塘河阶地上，其上部主要为块碎石土、角砾土等松散堆积物，整个坡体为松散坡体结构。

地震对边坡稳定性的影响首先表现为对岩土体力学性质的弱化效应，分为累计效应和触发效应两方面。前者主要表现为强烈的地震动使堆积碎石土颗粒之间的咬合程度降低，引起坡体结构松动，破裂面、软弱面错动和孔隙水压力累计上升等。后者则主要表现为地震作用造成边坡软弱层的触变液化，使软弱层岩土体力学性质弱化。

在力学机制上，巨大的地震惯性力给坡体施加了水平和竖向附加荷载，改变了坡体的原始静力平衡，导致山体出现滑坡。

强震过程中，边坡各个部位对地震的响应程度并不一样。坡顶的动力加速度放大效应比坡脚要大，这种坡顶的放大效应造成坡体内的瞬时拉应力，使得边坡的坡肩或陡坡部位一定范围产生弧形裂缝。如图1中的地震裂缝区和裂缝带，绝大部分发生在陡坎地段。这种裂缝虽然没有直接导致边坡失稳，但弱化了坡体结构，为震后降雨的入渗创造了条件，不利于边坡的长期稳定。

3 滑坡动力失稳定量分析

现场调查得到的动力失稳机理定性分析，有利于认识地震滑坡动力失稳原因，从而确定出滑坡稳定性的影响因素，为工程治理设计指明方向。但是，定性认识并不能确定地震作用对滑坡动力稳定性的影响过程，不能回答稳定性系数降低的程度以及滑面各部分降低的差异性问题，不能定量分析滑坡的动力失稳。

3.1 计算模型

选取滑坡主轴断面(图2)建立数值计算模型，尺寸如图3(a)所示。计算模型总长350.66 m，厚89.83 m。划分为滑体、滑带和滑床3种材料。为进行数值解析，模型共离散为489个单元和1 110个节点，如图 3(b)所示。

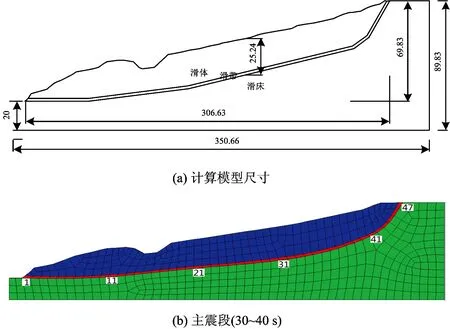
图3 主轴断面模型

3.2 地震荷载

2010年4月14日玉树地震时，距离玉树市结古镇约19 km的玉树机场强震观测台站获得了丰富的强震动数据。考虑到机场路滑坡倾向东，其动力稳定性受控于东西向地震动，因此，本文分析滑坡动力稳定性时，地震动输入选用EW向地震动分量。

EW向地震波如图4(a)所示。地震动强烈的时段集中在20～48 s，且在30～40 s时段震动最为强烈，加速度峰值远超其余时段。可以认为，30～40 s时段震动对滑坡动力稳定性具有决定性作用，为便于分析，可选择这一时段的动力输入作为代表，据此进行滑坡动力时程分析，该时段的加速度时程如图4(b)所示。

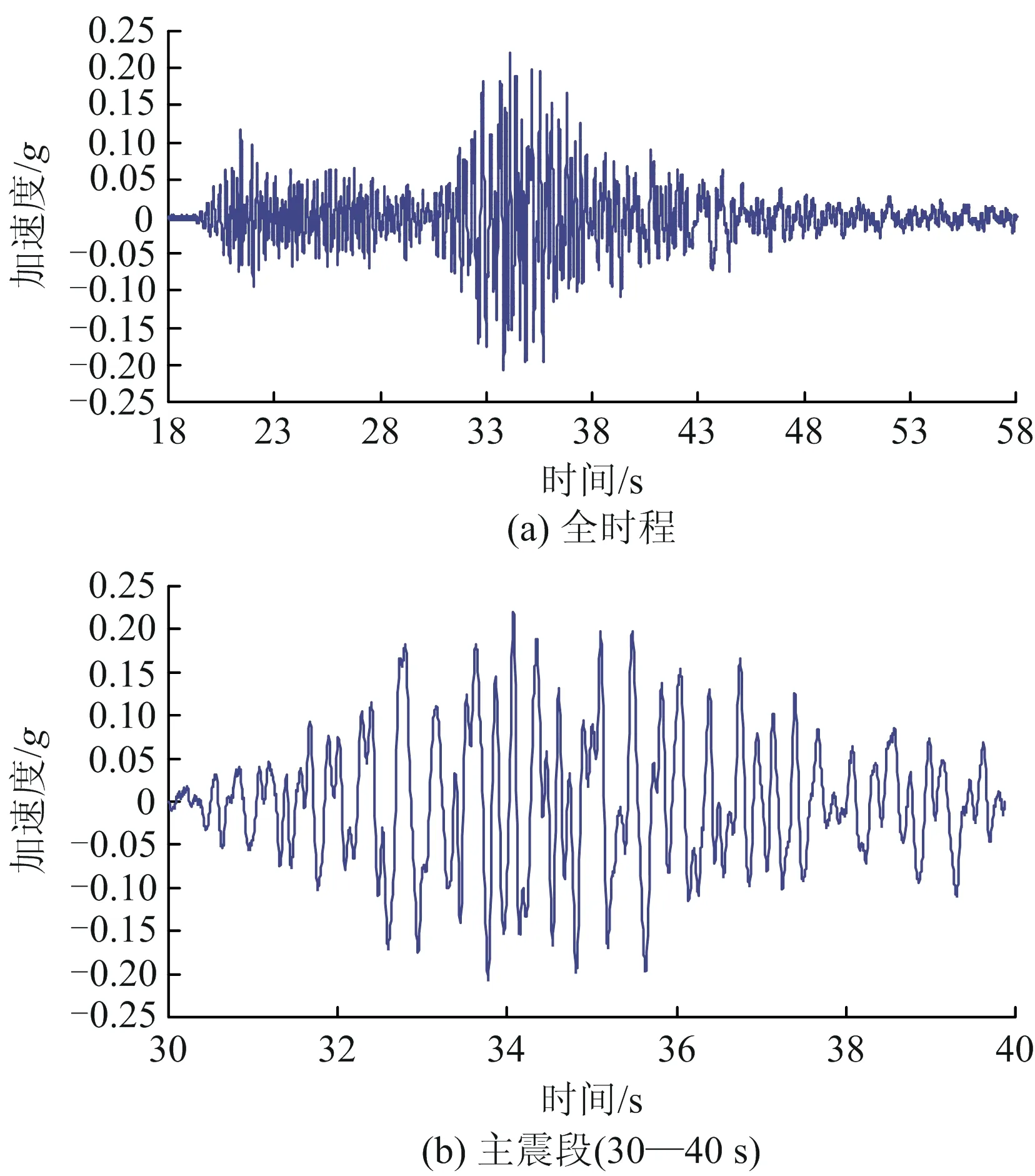
图4 加速度时程

3.3 动力时程

选用FLAC3D软件进行动力时程分析，动力边界采用自由场边界，进行全塑性分析，土体本构模型选用Mohr-Coulomb本构模型[18-19]。根据现场调查并结合反分析，滑带抗剪强度参数黏聚力取14 kPa，内摩擦角取12°，动力作用结束后的残余强度参数为：黏聚力12 kPa，内摩擦角10°。各计算参数见表1。

表1 岩体计算参数

对于滑坡动力失稳而言，其失稳过程主要体现在滑带稳定性上，因此提出采用滑带点安全系数对其动态稳定性进行评价。滑带点安全系数定义在滑带单元上，滑带单元编号如图3(b)所示。滑带离散为47个单元，图中示出了代表性单元编号，其余单元编号可据此推知。

3.4 滑带单元稳定性的动态演化

地震作用是连续动力作用过程，本文按0.067 s的时间间隔计算每一滑带单元的点安全系数，以及整体安全系数。

对每一滑带单元，在历时10 s的地震作用过程中，其单元应力在不断变化，滑带不断损伤，抗剪强度参数也不断降低，因此点安全系数也处于动态变化之中。研究单元点安全系数的动态时程变化，有利于分析该单元处滑带的动态稳定性，并由此分析滑坡的动力失稳机理。图5示出了代表性滑带单元的点安全系数时程曲线。

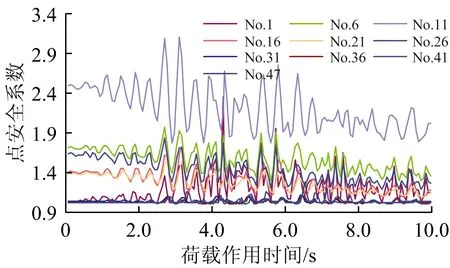
图5 点安全系数时程曲线

由滑带单元的点安全系数时程曲线可知：

(1)点安全系数随动力作用过程呈周期性变化。任何单元的点安全系数曲线均揭示了这一特性。最大点安全系数达到3.4以上，最小为1.0左右。

(2)在同一地震波作用周期(从正值变为负值，作用方向变化1次)，滑带各单元点安全系数并非同时达到最大值，存在滞后现象。如图6所示，图6给出的是滑带中具有不同高度的3点，其中5号单元位于滑带前部，高度最低，23号单元位于滑带中部，高度居中，47号单元位于滑带后部，高度最高。对于某一地震周期，5号单元达到点安全系数极大值(1.831)的时刻为2.702 s，23号单元达到极大值(1.519)的时刻为2.768 s，而47号单元达到极大值(1.091)的时刻却是2.900 s。显然可见，高度越低的滑带部分，越先到达峰值，相反，高度越高的滑带部分，则越滞后到达峰值。这反映了地震波在岩体中的传播过程。

(3)同一单元总体上点安全系数具有逐渐减小的趋势。当单元点安全系数大于1.2以上时，这种趋势最为明显。如7—24号单元最为明显。而当点安全系数接近1.0，位于1.0～1.1之间时，这种减小趋势不明显，如滑坡后部的31—47号单元。

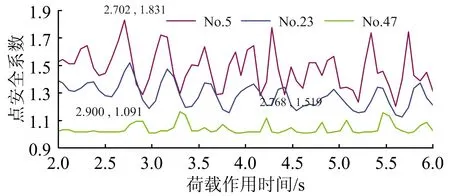
图6 点安全系数滞后现象

3.5 滑坡整体稳定性的动态演化

整体安全系数随动力作用过程而起伏变化，但整体趋势是逐渐减小。图7示出了整体安全系数随动力时程的变化曲线，从图7更容易看到，整体安全系数随动力作用过程而不断下降的趋势。

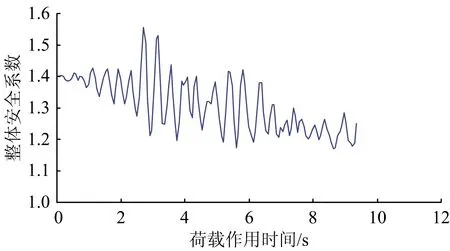
图7 整体安全系数演变时程

3.6 空间失稳机理

同一时刻，不同单元点安全系数的空间分布反映了滑带的空间稳定性，即不同部位的稳定性，有利于定量分析滑坡的动力失稳机理。

图8示出了地震过程中不同时刻滑带点安全系数的空间分布。由于地震作用时刻较长，每一单元记录的时间点有152个，因此不可能列出所有时间点的空间分布。图中仅列出了代表性的时间点。

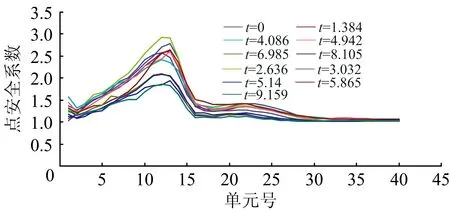
图8 地震过程中不同时刻点安全系数空间分布

由图8可知：

(1)自重静力状态下，2#滑泼滑动机理呈典型的推动式滑移特征。在最初时刻，点安全系数在滑坡前部较大(1号单元～17号单元段)，最大值达到2.3以上。而滑坡后部点安全系数均较小，18号单元以后，均小于1.3，后端几乎接近1.0。

(2)地震过程没有改变滑坡的整体滑动机理。即地震作用导致滑坡失稳下滑，其滑动机理与静力失稳机理基本一致，均为推动式。滑带上点安全系数分布始终保持前部较大，后部较小的形态。但是，从点安全系数的降低幅度来看，中前部降低明显，如单元12，点安全系数由2.916降到1.866，降低了30%。

这种点安全系数的分布和衰减规律与宏观变形现象相吻合。地震前滑坡即表现为后缘的圈椅状地形和多级陡坎，表明滑体后部稳定性较差，滑坡具有推动式滑动机理。地震作用下，滑体中前部西杭引水渠附近出现密集的裂缝带，这是由于其稳定性快速衰减所致。

4 结 语

采用FLAC3D程序进行滑坡动力时程数值分析，将滑带单元应力分解为垂直滑带的正应力和平行滑动方向的剪应力，据此定义滑带单元点安全系数以及对滑带面积进行加权平均的整体安全系数。

以点安全系数为指标，分析各滑带单元的点安全系数和滑坡整体安全系数的动态演化，以及滑带点安全系数空间分布形态的动态演化，定量判断滑坡的动力失稳。

玉树机场路2#滑坡的实例分析表明，该滑坡在自重下具有推动式滑移特征，地震作用没有改变其滑动机理。地震作用下，该滑坡滑带的单元点安全系数和整体安全系数均随动力作用过程而降低，且滑坡中前部降低明显，最大降幅约30%。

实例计算结果与现场观测的滑坡震后宏观变形特征相吻合，滑体中前部西杭引水渠附近震后出现密集的裂缝带，正是由于该部位滑带稳定性在地震作用下快速衰减所致。说明采用动态点安全系数分析滑坡的动力失稳机理是正确的。